ACM数论之旅10---大组合数-卢卡斯定理（在下卢卡斯，你是我的Master吗？(。-`ω´-) ）

记得前几章的组合数吧

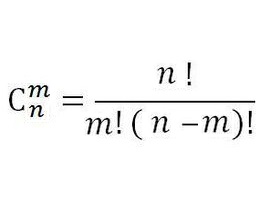
我们学了O(n^2)的做法，加上逆元，我们又会了O(n)的做法

现在来了新问题，如果n和m很大呢，

比如求C(n, m) % p  ， n<=1e18,m<=1e18,p<=1e5

看到没有，n和m这么大，但是p却很小，我们要利用这个p

（数论就是这么无聊的东西，我要是让n=1e100，m=1e100，p=1e100你有本事给我算啊(°□°)，还不是一样算不出来）

然后，我们著名的卢卡斯（Lucas）在人群中站了出来(｀･д･´)说：“让老子来教你这题”

卢卡斯说：

C(n, m) % p  =  C(n / p, m / p) * C(n%p, m%p) % p

对于C(n / p, m / p)，如果n / p 还是很大，可以递归下去，一直到世界的尽头

众人闻此言，无不惊叹，妙哉！妙哉！

（笑死我了o(*≧▽≦)ツ┏━┓拍桌狂笑）

（不要问我证明过程，我不费(´･ω･｀)）

然后上代码

 LL Lucas(LL n, LL m, int p){
         return m ? Lucas(n/p, m/p, p) * comb(n%p, m%p, p) % p : ;
 }

简洁易懂<(￣︶￣)>

实战一下吧

hdu 5446

http://acm.hdu.edu.cn/showproblem.php?pid=5446

题意：

给你三个数n, m, k

第二行是k个数，p1,p2,p3...pk

所有p的值不相同且p都是质数

求C(n, m) % (p1*p2*p3*...*pk)的值

范围：1≤m≤n≤1e18，1≤k≤10，pi≤1e5，保证p1*p2*p3*...*pk≤1e18

AC代码：

 #include<cstdio>
 typedef long long LL;
 const int N =  + ;
 LL mul(LL a, LL b, LL p){//快速乘，计算a*b%p
     LL ret = ;
     while(b){
         if(b & ) ret = (ret + a) % p;
         a = (a + a) % p;
         b >>= ;
     }
     return ret;
 }
 LL fact(int n, LL p){//n的阶乘求余p
     LL ret = ;
      for (int i = ; i <= n ; i ++) ret = ret * i % p ;
     return ret ;
 }
 void ex_gcd(LL a, LL b, LL &x, LL &y, LL &d){
     if (!b) {d = a, x = , y = ;}
     else{
         ex_gcd(b, a % b, y, x, d);
         y -= x * (a / b);
     }
 }
 LL inv(LL t, LL p){//如果不存在，返回-1
     LL d, x, y;
     ex_gcd(t, p, x, y, d);
     return d ==  ? (x % p + p) % p : -;
 }
 LL comb(int n, int m, LL p){//C(n, m) % p
     if (m <  || m > n) return ;
     return fact(n, p) * inv(fact(m, p), p) % p * inv(fact(n-m, p), p) % p;
 }
 LL Lucas(LL n, LL m, int p){
         return m ? Lucas(n/p, m/p, p) * comb(n%p, m%p, p) % p : ;
 }
 LL china(int n, LL *a, LL *m){//中国剩余定理
     LL M = , ret = ;
     for(int i = ; i < n; i ++) M *= m[i];
     for(int i = ; i < n; i ++){
         LL w = M / m[i];
         //ret = (ret + w * inv(w, m[i]) * a[i]) % M;//这句写了会WA，用下面那句
         ret = (ret + mul(w * inv(w, m[i]), a[i], M)) % M;
         //因为这里直接乘会爆long long ,所以我用快速乘(unsigned long long也是爆掉，除非用高精度)
     }
     return (ret + M) % M;
 }
 int main(){
     int T, k;
     LL n, m, p[], r[];
     scanf("%d", &T);
     while(T--){
         scanf("%I64d%I64d%d", &n, &m, &k);
         for(int i = ; i < k; i ++){
             scanf("%I64d", &p[i]);
             r[i] = Lucas(n, m, p[i]);
         }
         printf("%I64d\n", china(k, r, p));
     }
 }

我们知道题目要求C(n, m) % (p1*p2*p3*...*pk)的值

其实这个就是中国剩余定理最后算出结果后的最后一步求余

那C(n, m)相当于以前我们需要用中国剩余定理求的值

然而C(n, m)太大，我们只好先算出

C(n, m) % p1 = r1

C(n, m) % p2 = r2

C(n, m) % p3 = r3

.

.

.

C(n, m) % pk = rk

用Lucas，这些r1,r2,r3...rk可以算出来

然后又是用中国剩余定理求答案

全都是套路。。。