Python 爬虫-正则表达式
2017-07-27 13:52:08
一、正则表达式的概念
(1)正则表达式是用来简洁表达一组字符串的表达式,最主要应用在字符串匹配中。
- 正则表达式是用来简洁表达一组字符串的表达式
- 正则表达式是一种通用的字符串表达框架
- 正则表达式是一种针对字符串表达“简洁”和“特征”思想的工具
- 正则表达式可以用来判断某字符串的特征归属
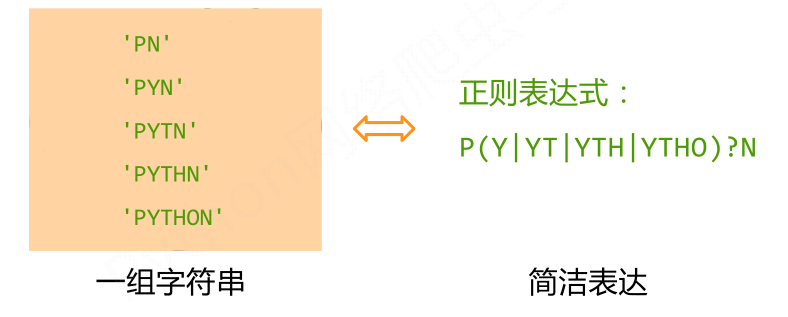
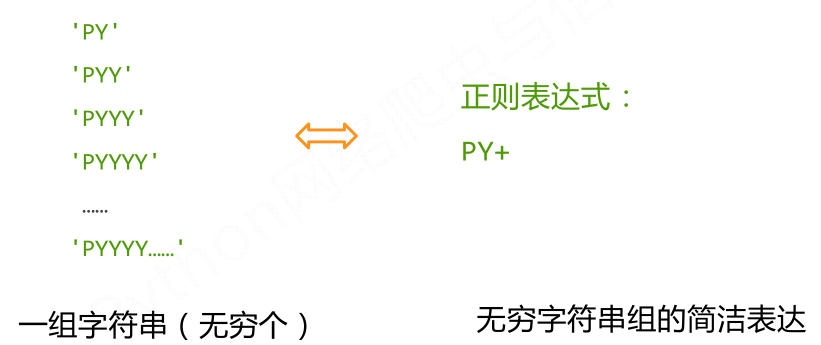

(2)正则表达式是一个字符串,通过编译将符合正则表达式语法的字符串转换成正则表达式特征。

二、正则表达式的语法
正则表达式语法由字符和操作符构成。
(1)正则表达式的操作符
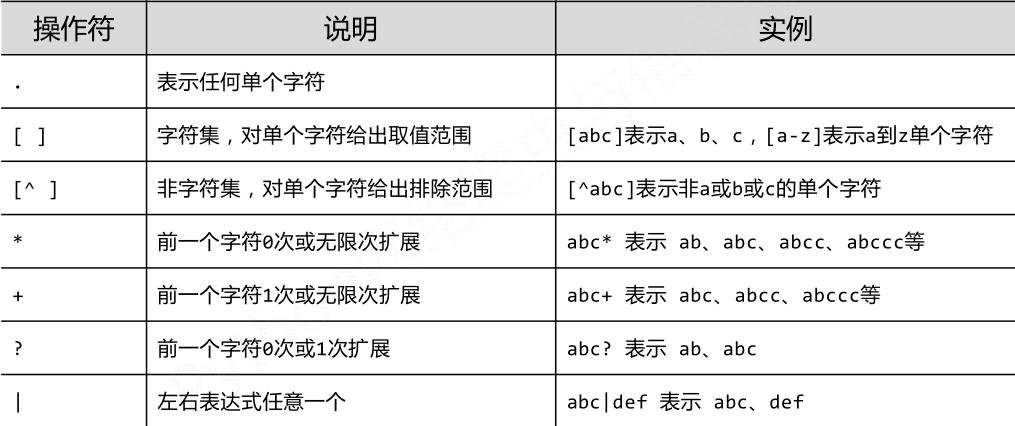
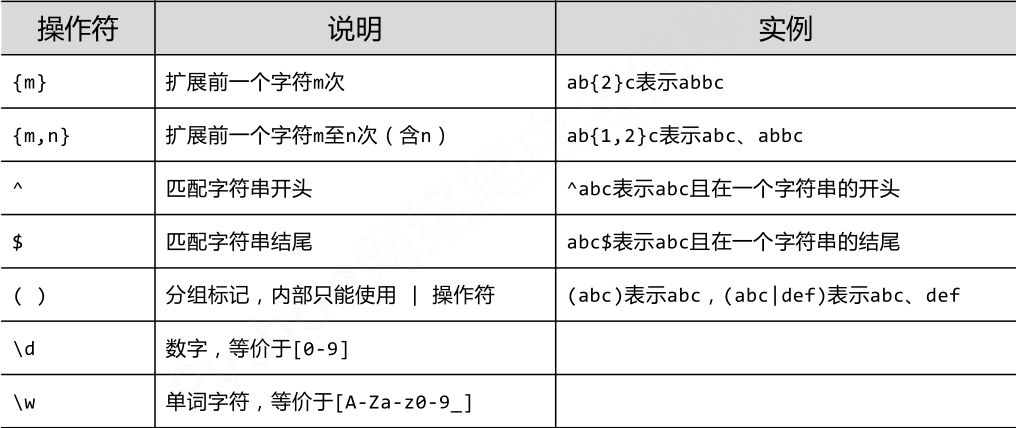
经典的正则表达式:


三、Re库的使用
re库采用原生字符串(raw string)来表达正则表达式。所谓原生字符串是指没有反义字符的字符串,也就是说在原生字符中‘\’就是反斜杠,不是转义。使用原生字符串只需要在字符串前加上r即可。
也可以使用正常的string字符串,不过使用string字符串的话需要很多的转义字符来表示单纯的反斜杠。
Re库的主要功能函数:

- re.search(pattern, string, flags=0):在一个字符串中搜索匹配正则表达式的第一个位置,返回match对象
∙ pattern : 正则表达式的字符串或原生字符串表示
∙ string : 待匹配字符串
∙ flags : 正则表达式使用时的控制标记


- re.match(pattern, string, flags=0):从一个字符串的开始位置起匹配正则表达式,返回match对象
∙ pattern : 正则表达式的字符串或原生字符串表示
∙ string : 待匹配字符串
∙ flags : 正则表达式使用时的控制标记

- re.findall(pattern, string, flags=0):搜索字符串,以列表类型返回全部能匹配的子串
∙ pattern : 正则表达式的字符串或原生字符串表示
∙ string : 待匹配字符串
∙ flags : 正则表达式使用时的控制标记

- re.split(pattern, string, maxsplit=0, flags=0):将一个字符串按照正则表达式匹配结果进行分割,返回列表类型
∙ pattern : 正则表达式的字符串或原生字符串表示
∙ string : 待匹配字符串
∙ maxsplit: 最大分割数,剩余部分作为最后一个元素输出
∙ flags : 正则表达式使用时的控制标记

- re.finditer(pattern, string, flags=0):搜索字符串,返回一个匹配结果的迭代类型,每个迭代元素是match对象
∙ pattern : 正则表达式的字符串或原生字符串表示
∙ string : 待匹配字符串
∙ flags : 正则表达式使用时的控制标记

- re.sub(pattern, repl, string, count=0, flags=0):在一个字符串中替换所有匹配正则表达式的子串,返回替换后的字符串
∙ pattern : 正则表达式的字符串或原生字符串表示
∙ repl : 替换匹配字符串的字符串
∙ string : 待匹配字符串
∙ count : 匹配的最大替换次数
∙ flags : 正则表达式使用时的控制标记

正则表达式的另一种等价用法,使用 compile () 函数:

经过了compile后的正则表达式可以使用如下函数,这里只需要给出需要匹配的字符串就可以了:

三、Re库的match对象
Match对象是一次匹配的结果,包含匹配的很多信息。
- match对象的属性
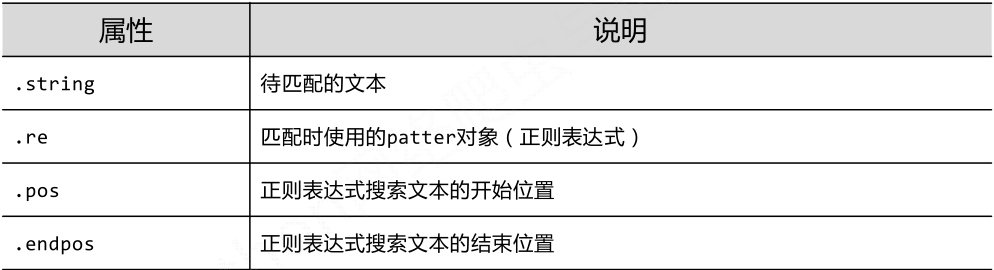
- match对象的方法

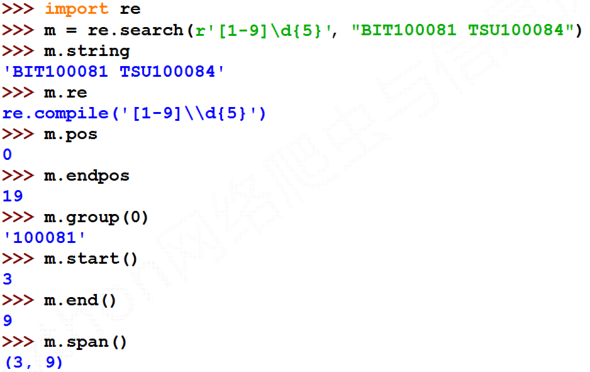
四、贪婪匹配与最小匹配
Re库默认采用贪婪匹配,即输出匹配最长的子串;
只要长度输出可能不同的,都可以通过在操作符后增加?变成最小匹配
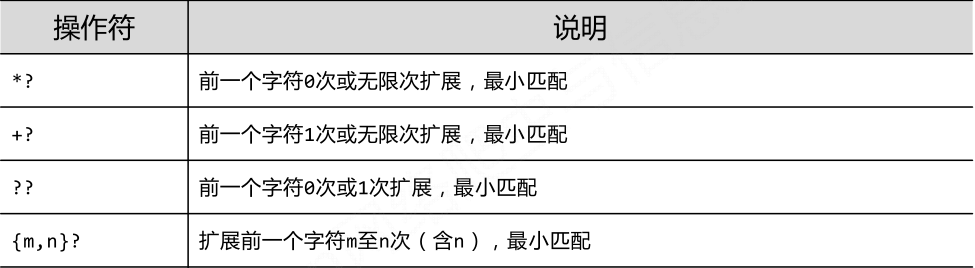
Python 爬虫-正则表达式的更多相关文章
- Python 爬虫-正则表达式(补)
2017-08-08 18:37:29 一.Python中正则表达式使用原生字符串的几点说明 原生字符串和普通字符串的不同 相较于普通字符串,原生字符串中的\就是反斜杠,并不表达转义.不过,字符串转成 ...
- Python爬虫 正则表达式
1.正则表达式概述 正则表达式是对字符串操作的一种逻辑公式,就是用事先定义好的一些特定字符.及这些特定字符的组合,组成一个"规则字符串",这个"规则字符串"用来 ...
- Python爬虫-正则表达式基础
import re #常规匹配 content = 'Hello 1234567 World_This is a Regex Demo' #result = re.match('^Hello\s\d\ ...
- python爬虫+正则表达式实例爬取豆瓣Top250的图片
直接上全部代码 新手上路代码风格可能不太好 import requests import re from fake_useragent import UserAgent #### 用来伪造爬头部信息 ...
- python爬虫之re正则表达式库
python爬虫之re正则表达式库 正则表达式是用来简洁表达一组字符串的表达式. 编译:将符合正则表达式语法的字符串转换成正则表达式特征 操作符 说明 实例 . 表示任何单个字符 [ ] 字符集,对单 ...
- python爬虫主要就是五个模块:爬虫启动入口模块,URL管理器存放已经爬虫的URL和待爬虫URL列表,html下载器,html解析器,html输出器 同时可以掌握到urllib2的使用、bs4(BeautifulSoup)页面解析器、re正则表达式、urlparse、python基础知识回顾(set集合操作)等相关内容。
本次python爬虫百步百科,里面详细分析了爬虫的步骤,对每一步代码都有详细的注释说明,可通过本案例掌握python爬虫的特点: 1.爬虫调度入口(crawler_main.py) # coding: ...
- python爬虫数据解析之正则表达式
爬虫的一般分为四步,第二个步骤就是对爬取的数据进行解析. python爬虫一般使用三种解析方式,一正则表达式,二xpath,三BeautifulSoup. 这篇博客主要记录下正则表达式的使用. 正则表 ...
- Python爬虫入门之正则表达式
在前面我们已经搞定了怎样获取页面的内容,不过还差一步,这么多杂乱的代码夹杂文字我们怎样把它提取出来整理呢?下面就开始介绍一个十分强大的工具,正则表达式! 1.了解正则表达式 正则表达式是对字符串操作的 ...
- Python爬虫与数据分析之爬虫技能:urlib库、xpath选择器、正则表达式
专栏目录: Python爬虫与数据分析之python教学视频.python源码分享,python Python爬虫与数据分析之基础教程:Python的语法.字典.元组.列表 Python爬虫与数据分析 ...
随机推荐
- php端口号设置和查看
- CAS机制
##################################################################### 我们知道多线程操作共享资源时,会出现三个问题:可见性.有序性 ...
- 模仿WIN32程序处理消息
#include "stdafx.h" #include "MyMessage.h" #include <conio.h> using namesp ...
- 形象易懂讲解算法I——小波变换
https://zhuanlan.zhihu.com/p/22450818?refer=dong5 最早发于回答:能不能通俗的讲解下傅立叶分析和小波分析之间的关系? - 咚懂咚懂咚的回答现收入专栏. ...
- $好玩的分词——python jieba分词模块的基本用法
jieba(结巴)是一个强大的分词库,完美支持中文分词,本文对其基本用法做一个简要总结. 安装jieba pip install jieba 简单用法 结巴分词分为三种模式:精确模式(默认).全模式和 ...
- 【CSS3】纯CSS代码实现模拟时钟,+js对时功能。
使用CSS3纯代码来实现模拟时钟,及指针动画功能. 在这里主要使用到css3一些基本元素: border-radius:圆角边框,画圆形:表盘 Transform:变换,旋转,扭曲:刻度盘,指针形状 ...
- Centos 更改系统时间
.date //查看本地 .hwclock --show //查看硬件的时间 .如果硬件的时间是对不上,那就对硬件的时间进行修改 .hwclock --set --date '2222-22-22 2 ...
- Confluence5.8更改数据库配置
Confluence5.8更改数据库配置 第一步:是找到confluence的安装目录,我的安装目录在 /opt/atlassian/: 第二步:由于confluence把tomcat给改造了,所以c ...
- JavaScript 中语法规范及调试
JavaScript 中语法规范及调试 版权声明:未经博主授权,内容严禁分享转载 JavaScript 开发环境 JavaScript 脚本可以使用任意一款纯文本编辑器进行编程开发. 常见的前端开发编 ...
- 20145301 赵嘉鑫 《网络对抗》Exp6 信息搜集与漏洞扫描
20145301赵嘉鑫<网络对抗>Exp6 信息搜集与漏洞扫描 基础问题回答 哪些组织负责DNS,IP的管理? 全球根服务器均由美国政府授权的ICANN统一管理,负责全球的域名根服务器.D ...
