[ABC205F] Grid and Tokens 题解

Grid and Tokens

题目大意

给定 \(n\) 个点和一个 \(H\times W\) 的网格，每个点可以放置在 \((A_i,B_i)\) 到 \((C_i,D_i)\) 的矩形中或不放，每一行或一列只能放置一个点，求最多能放多少个点。

思路分析

首先看数据范围，再结合题目给的限制条件，容易发现这是一道网络流。

考虑建图，因为行和列存在限制条件而网格中的点不存在，所以可以考虑将每一行和每一列分别建成一个点。再建立一个超级源点和超级汇点，源点向行连边权为 \(1\) 的边，列向汇点连边权为 \(1\) 的边。 表示每一行和每一列只能放一个点的限制条件。

对于一个点的矩形放置范围，可以转换为行 \(A_i\sim C_i\) 向该点连边权为 \(1\) 的边，该点向列 \(B_i\sim D_i\) 连边权为 \(1\) 的边，表示每一行和每一列对于点的匹配。

同时，点存在容量的限制，所以要将点拆成入点和出点，再连边。

综上所述，建图过程如下：

• 建立源点，汇点。

• 对于每一行和每一列建立一个点，源点向行连边权为 \(1\) 的边，列向汇点连边权为 \(1\) 的边。

• 对于每一个点，建立入点和出点，入点向出点连边权为 \(1\) 的边，行 \(A_i\sim C_i\) 向入点连边权为 \(1\) 的边，出点向列 \(B_i\sim D_i\) 连边权为 \(1\) 的边。

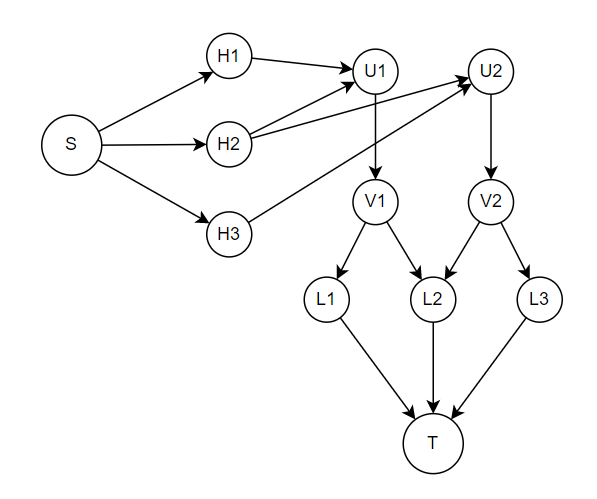
因为流网络是单位网络，所以时间复杂度为 \(O(n^3)\)。(\(n,H,W\) 同阶)

代码

#include <iostream>
#include <cmath>
#include <cstring>
#include <algorithm>
#include <cstdio>
#include <queue>

using namespace std;
const int N=200100;
#define inf 0x3f3f3f3f

int n,m,k,idx=1,S,T,in1,in2,in3,in4,cnt;
int to[N],nxt[N],head[N],w[N];
int cur[N],d[N];

queue <int> q;

void add(int u,int v,int c){
    idx++;to[idx]=v;nxt[idx]=head[u];head[u]=idx;w[idx]=c;
    idx++;to[idx]=u;nxt[idx]=head[v];head[v]=idx;w[idx]=0;
}

bool bfs(){
    memset(d,-1,sizeof d);
    while(!q.empty()) q.pop();
    cur[S]=head[S];
    q.push(S);d[S]=0;
    while(!q.empty()){
        int now=q.front();q.pop();
        for(int i=head[now];i;i=nxt[i]){
            int v=to[i];
            if(~d[v]||!w[i]) continue;
            d[v]=d[now]+1;
            cur[v]=head[v];
            if(v==T) return 1;
            q.push(v);
        }
    }
    return 0;
}

int dfs(int s,int lim){
    if(s==T) return lim;
    int flow=0;
    for(int i=cur[s];i&&flow<lim;i=nxt[i]){
        int v=to[i];cur[s]=i;
        if(d[v]!=d[s]+1||!w[i]) continue;
        int t=dfs(v,min(w[i],lim-flow));
        if(!t) d[v]=-1;
        w[i]-=t;w[i^1]+=t;flow+=t;
    }
    return flow;
}

int dinic(){
    int ans=0,flow=0;
    while(bfs()) while(flow=dfs(S,inf)) ans+=flow;
    return ans;
}

int main(){
    scanf("%d%d%d",&n,&m,&k);
    S=N-5;T=N-6;cnt=n+m+1;
    for(int i=1;i<=n;i++) add(S,i,1);//源点->行
    for(int i=n+1;i<=n+m;i++) add(i,T,1);//列->汇点
    for(int i=1;i<=k;i++){
        scanf("%d%d%d%d",&in1,&in2,&in3,&in4);
        for(int i=in1;i<=in3;i++) add(i,cnt,1);//行->入点
        for(int i=n+in2;i<=n+in4;i++) add(cnt+1,i,1);//出点->列
        add(cnt,cnt+1,1);//入点->出点
        cnt+=2;
    }
    cout<<dinic()<<'\n';
    return 0;
}