0x62 图论-最小生成树

A题：走廊泼水节

链接：https://ac.nowcoder.com/acm/contest/1056/A

题目描述

给定一棵N个节点的树，要求增加若干条边，把这棵树扩充为完全图，并满足图的唯一最小生成树仍然是这棵树。

求增加的边的权值总和最小是多少。

输入描述:

第一行包含整数t，表示共有t组测试数据。
对于每组测试数据，第一行包含整数N。
接下来N-1行，每行三个整数X,Y,Z，表示X节点与Y节点之间存在一条边，长度为Z。

输出描述:

每组数据输出一个整数，表示权值总和最小值。

每个结果占一行。

示例1

输入

2
3
1 2 2
1 3 3
4
1 2 3
2 3 4
3 4 5

输出

4
17

备注:

\[N <= 6000 , Z <= 100
\]

例解释

第一组数据，在 22 和 33 之间修建一条长度为 44 的道路，

使这棵树变成一个完全图，且原来的树依然是这个图的唯一最小生成树.

　

题解

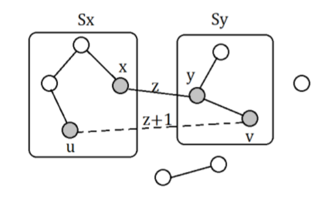
• 对给定树上的 \(N−1\) 条边模拟一遍\(Kruskal\)
• 通过边$(x,y) $合并两个并查集
• xx 集合中的每个点到 \(y\) 集合中的每个点
• 添加一条长度为 $w(x,y)+1 $的边

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
#define maxn 6010
struct edge{ int u,v,w; }e[maxn];
int t,n,f[6010],s[6010];
long long ans;
bool cmp(edge x,edge y){ return x.w<y.w; }
int find(int x){
	if(f[x]!=x) f[x]=find(f[x]);
	return f[x];
}
int main(){
	scanf("%d",&t);
	while(t--){
		scanf("%d",&n);
		for(int i=1;i<=n;++i){ f[i]=i; s[i]=1; }
		for(int i=1;i<n;++i) scanf("%d %d %d",&e[i].u,&e[i].v,&e[i].w);
		sort(e+1,e+n,cmp);
		ans=0;
		for(int fu,fv,i=1;i<n;++i){
			fu=find(e[i].u); fv=find(e[i].v);
			if(fu==fv) continue;
			ans+=1ll*(e[i].w+1)*(s[fu]*s[fv]-1);
			f[fu]=fv;
			s[fv]+=s[fu];
		}
		printf("%lld\n",ans);
	}
	return 0;
}

B题：Picnic Planning (控制度数的最小生成树，DFS)

https://ac.nowcoder.com/acm/contest/1056/B

#include <bits/stdc++.h>
using namespace std;
#define js ios::sync_with_Bstdio(false);cin.tie(0); cout.tie(0)
typedef long long ll;

inline int read() {
    int s = 0, w = 1; char ch = getchar();
    while (ch < 48 || ch > 57) { if (ch == '-') w = -1; ch = getchar(); }
    while (ch >= 48 && ch <= 57) s = (s << 1) + (s << 3) + (ch ^ 48), ch = getchar();
    return s * w;
}
const int N = 37;
const int INF = 0x3f3f3f3f;
struct Edge {
    int x, y, z;
    bool operator < (const Edge w) const {
        return z < w.z;
    }
}f[N];
int n, k, tot, ans, a[N][N], fa[N], d[N], v[N];
map<string, int> mp;
vector<Edge> e;
bool b[N][N];

int find(int x) {
    return fa[x] == x ? x : fa[x] = find(fa[x]);
}

void dfs(int x, int pre) {
    for (int i = 2; i <= tot; ++i) {
        if (i == pre || !b[x][i])   continue;
        if (f[i].z == -1) {
            if (f[x].z > a[x][i])    f[i] = f[x];
            else {
                f[i].x = x;
                f[i].y = i;
                f[i].z = a[x][i];
            }
        }
        dfs(i, x);
    }
}

int main() {
    js;
    memset(a, 0x3f, sizeof(a));
    memset(d, 0x3f, sizeof(d));
    mp["Park"] = tot = 1;
    for (int i = 1; i < N; ++i)  fa[i] = i;
    cin >> n;
    for (int i = 1; i <= n; ++i) {
        Edge w;
        string s1, s2;
        cin >> s1 >> s2 >> w.z;
        w.x = mp[s1] ? mp[s1] : (mp[s1] = ++tot);
        w.y = mp[s2] ? mp[s2] : (mp[s2] = ++tot);
        e.push_back(w);
        a[w.x][w.y] = a[w.y][w.x] = min(a[w.x][w.y], w.z);
    }
    cin >> k;
    sort(e.begin(), e.end());
    for (auto it : e) { //去掉1的连边，构成几个连通块，再把连通块并成一个求解花费
        if (it.x == 1 || it.y == 1) continue;
        int fax = find(it.x), fay = find(it.y);
        if (fax != fay) {
            fa[fax] = fay;
            b[it.x][it.y] = b[it.y][it.x] = 1;
            ans += it.z;
        }
    }
    for (int i = 2; i <= tot; ++i) //找连通区域内和1连接花费最小
        if (a[1][i] != INF) {
            int rt = find(i);
            if (d[rt] > a[1][i]) {
                v[rt] = i;
                d[rt] = a[1][v[rt]];
            }
        }
    for (int i = 1; i <= tot; ++i) { //先把连通区域和1连接
        if (d[i] != INF) {
            --k;
            b[1][v[i]] = b[v[i]][1] = 1;
            ans += a[1][v[i]];
        }
    }
    while (k--) { //调整看能不能更小一点
        memset(f, -1, sizeof(f));
        f[1].z = -INF;
        for (int i = 2; i <= tot; ++i)
            if (b[1][i])    f[i].z = -INF;
        dfs(1, 0);
        int o, w = -INF;
        for (int i = 2; i <= tot; ++i)
            if (w < f[i].z - a[1][i]) {
                o = i;
                w = f[i].z - a[1][o];
            }
        if (w <= 0)  break;
        b[1][o] = b[o][1] = 1;
        b[f[o].x][f[o].y] = b[f[o].y][f[o].x] = 0;
        ans -= w;
    }
    cout << "Total miles driven: " << ans << endl;
    return 0;
}

C题：最优比率生成树

https://ac.nowcoder.com/acm/contest/1056/C

0/1 规划问题，利用二分 + prim求解。

根据0/1问题模型，只需要构建一张新的无向网，图的结构不变，但每条边只有一个权值 \(C_e - mid * R_e\) ，在新的无向图中求解最大生成树，若最大生成树上边权之和非负，$l = mid $,否则令 \(r = mid\)。

#include<bits/stdc++.h>
using namespace std;
#define dis(a,b)  sqrt(pow((nod[a].x - nod[b].x), 2) + pow((nod[a].y - nod[b].y), 2))
const int maxn = 5000;
const int inf = 0x3f3f3f3f;
struct node {
	double x, y, c;
}nod[maxn];
int n;
double cost[maxn][maxn];
double a[maxn][maxn];
bool book[maxn];
double d[maxn];

double  prim(double mid) {
    memset(book, 0, sizeof(book));
    for (int i = 1; i <= n; i++)
        d[i] = 1e8;
    d[1] = 0;
    for (int i = 1; i < n; i++) {//一共只需要进行n-1次操作
        int x = 0;
        for (int j = 1; j <= n; j++)
            if (!book[j] && (x == 0 || d[x] > d[j]))//找出没有用过或者距离已选遍最近的点
                x = j;
        book[x] = true;
        for (int y = 1; y <= n; y++)
            if (!book[y])d[y] = min(d[y], a[x][y] - mid * cost[x][y]);
    }
    double  ans = 0.0;
    for (int i = 2; i <= n; i++) {
        ans += d[i];
    }
    return ans;
}

int main() {
	//freopen("in.txt", "r", stdin);
	//ios::sync_with_stdio(false), cin.tie(0);
    while (scanf("%d", &n), n) {
        for (int i = 1; i <= n; i++)
            scanf("%lf%lf%lf", &nod[i].x, &nod[i].y, &nod[i].c);

        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= n; j++) {
                cost[i][j] = dis(i, j);
                a[i][j] = fabs(nod[i].c - nod[j].c);
            }

        double r = inf, l = 0;
        while (r - l > 0.000001) {
            double mid = (l + r) / 2;
            double ans = prim(mid);
            if (ans == 0)
                break;
            else if (ans > 0)
                l = mid;
            else
                r = mid;
        }
        printf("%.3lf\n", (r + l) / 2);
    }
}

D题：黑暗城堡 （最短路径生成树）

先跑一次dijkstra

对于构造一个树的过程，每个节点都会选择一个节点插入树中

只需要统计每个点能够选择哪些点（满足到1号点距离最小）去插入即可。

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e3+10;
int e[maxn][maxn],inf=1e9;
int dis[maxn],vis[maxn];
const int mod=(1LL<<31)-1;
struct node
{
    int s,id;
    bool operator < (const node& b) const{
        return (this->s)<b.s;
    }
}q[maxn];
int main()
{
    int n,m;scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++){
        for(int j=1;j<i;j++)
            e[i][j]=e[j][i]=inf;
    }
    for(int i=1;i<=m;i++){
        int t1,t2,t3;
        scanf("%d%d%d",&t1,&t2,&t3);e[t1][t2]=e[t2][t1]=t3;
    }
    for(int i=1;i<=n;i++)    dis[i]=inf;
    dis[1]=0;
    for(int i=1;i<n;i++){
        int u,mx=1e9;
        for(int j=1;j<=n;j++){
            if(vis[j])  continue;
            if(dis[j]<mx){
                u=j;mx=dis[j];
            }
        }
        vis[u]=1;
        for(int j=1;j<=n;j++){
            if(dis[j]>dis[u]+e[u][j]){
                dis[j]=dis[u]+e[u][j];
            }
        }
    }
    for(int i=1;i<=n;i++){
        q[i].s=dis[i];q[i].id=i;
    }
    sort(q+1,q+1+n);int ans=1;
    for(int i=2;i<=n;i++){
        int cnt=0;
        for(int j=1;j<=n;j++){
            if(j==i)    continue;
            if(dis[i]==dis[j]+e[j][i])  cnt++;
        }
        //cout<<i<<" "<<cnt<<endl;
        ans=1LL*ans*cnt%mod;
    }
    cout<<ans<<endl;
}