2023.09.29 入门级 J2 模拟赛 赛后总结（尝试第一篇总结）

T1：变换(change)

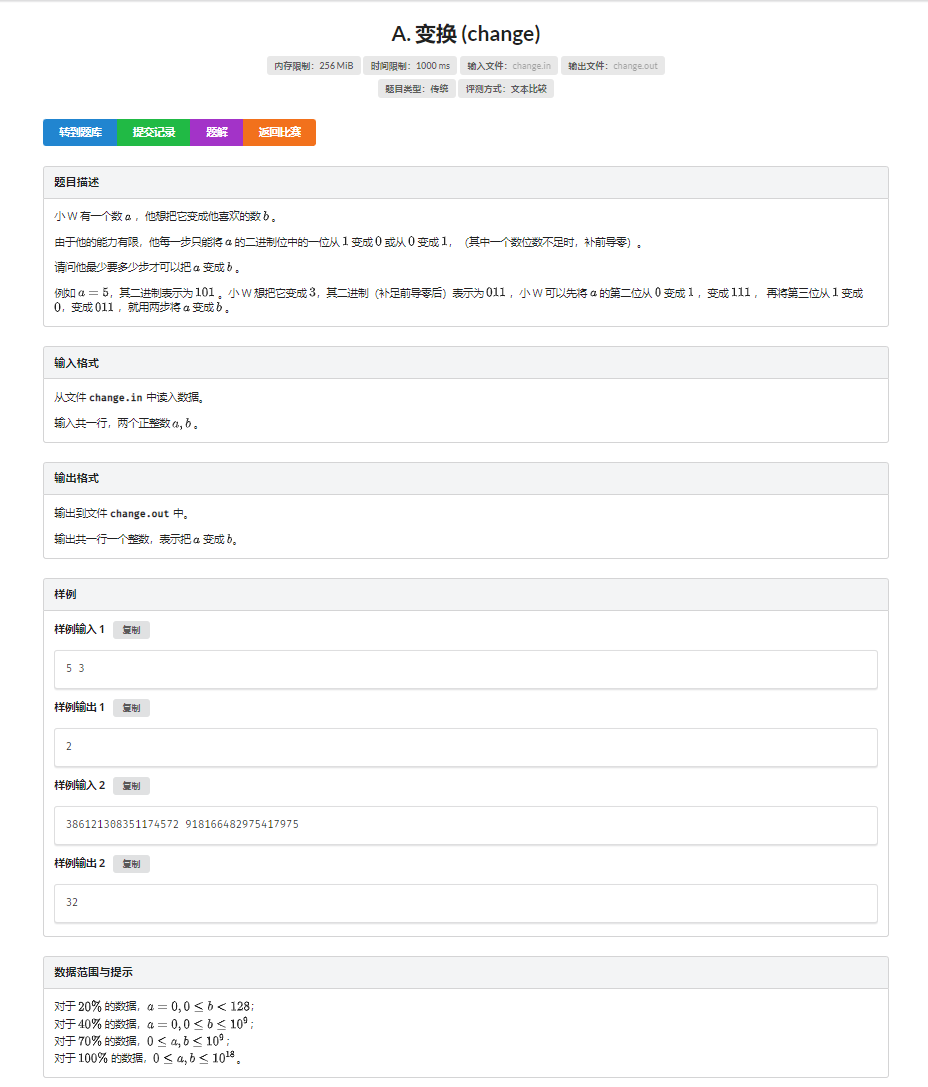
一道大水题.

赛场上想都没想就切掉了

不难发现，转换的过程只和a 和b 的二进制位有关，且不同二进制位之间无关。我们可以将a 和b 转化为二进制表示，每一位分别判断，如果这位不同，答案+1

更快的方法

可以发现对于每一位，如果a,b的这位相同，异或值为0 ，如果不同，异或值为1 。所以答案为 a异或 b的二进制 1的个数。

AC CODE

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 int main(){
 4     freopen("change.in", "r", stdin);
 5     freopen("change.out", "w", stdout);
 6     long long a, b;
 7     scanf("%lld%lld", &a, &b);
 8     printf("%d\n", __builtin_popcountll(a ^ b));
 9     return 0;
10 }

PS:__builtin_popcount()函数可以在O(1)的复杂的计算一个数二进制 1的个数而__builtin_popcountll() 是其的 long long 版本。

T2:打地鼠 (mouse)

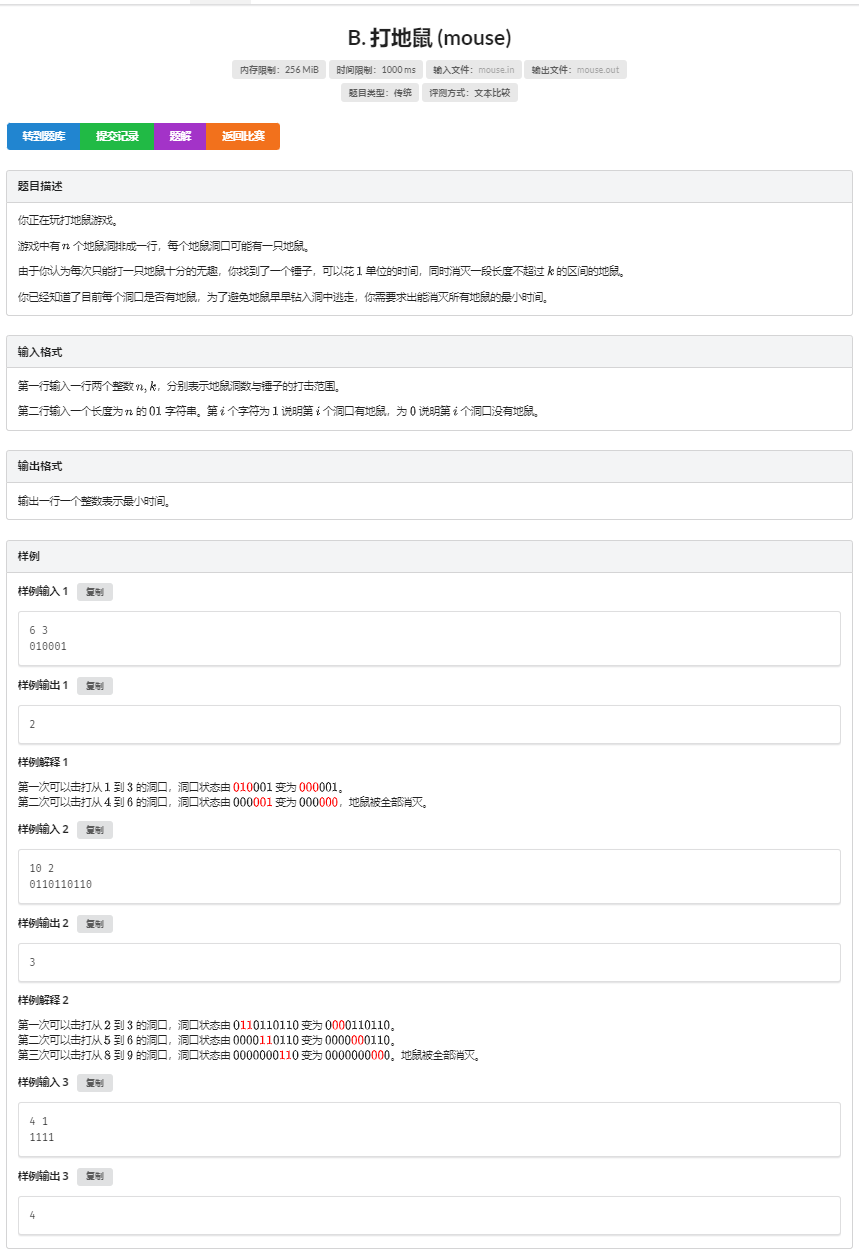
赛场上略加思考就切掉了

简单贪心，每次找到位置最靠前的未被消灭的地鼠 ，对i~i+k-1的地鼠进行打击。 

AC CODE

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 const int N=2e5+10;
 4 int n,k,ans;
 5 char s[N];
 6 int main(){
 7     freopen("mouse.in","r",stdin);
 8     freopen("mouse.out","w",stdout);
 9     scanf("%d%d%s",&n,&k,s+1);ans=0;
10     for(int i=1;i<=n;++i)
11     if(s[i]=='1') ++ans,i+=k-1;
12     printf("%d\n",ans);
13     return 0;
14 }

还是来证明一下吧，不然文章太短了(￣▽￣)"

用反证法，假设不按这种方式进行贪心，那么打击范围会有重复即贡献会有重复，造成浪费，因此当前方式即为最优解！

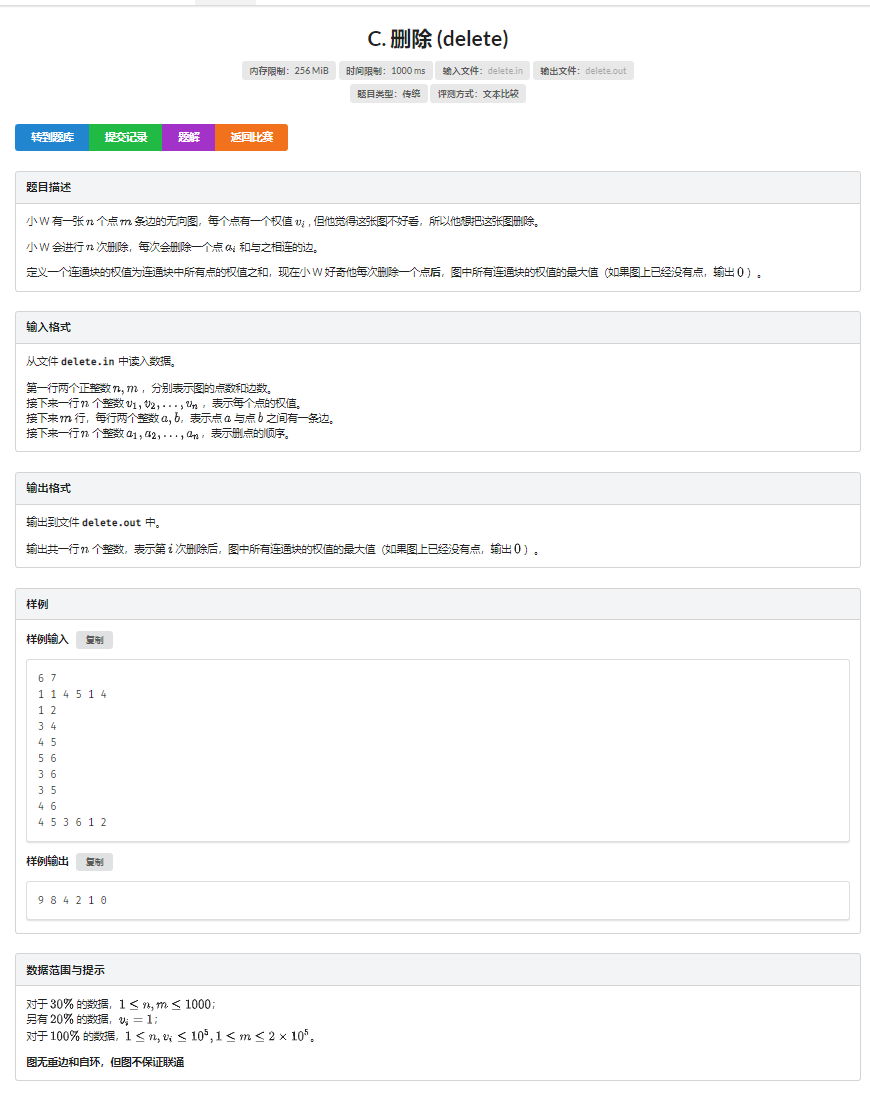
T3：删除(delete)

正难则反，考虑删图的逆过程，要是让我正着来我也不会啊ε=ε=ε=(~￣▽￣)~溜了溜了，每次加入一个点，就将和它相连的的已经加入的点的连通块并成一个新的连通

块。连通块及其的权值可以用并查集维护。

AC CODE

 1 #include <bits/stdc++.h>
 2 #define ll long long
 3 using namespace std;
 4 const int N = 1e5 + 5;
 5 vector<int> to[N];
 6 bool flag[N];
 7 ll total[N], mx, value[N], a[N], fa[N], u, v;
 8 int find(int x) { return fa[x] == x ? x : fa[x] = find(fa[x]); }
 9 int main() {
10     freopen("delete.in", "r", stdin);
11     freopen("delete.out", "w", stdout);
12     int n, m;
13     cin >> n >> m;
14     for (int i = 1; i <= n; i++) cin >> value[i];
15     while (m--) {
16         cin >> u >> v;
17         to[u].push_back(v);
18         to[v].push_back(u);
19     }
20     for (int i = n; i; i--) cin >> a[i];
21     vector<long long> ans = { 0 };
22     for (int i = 1; i <= n; i++) fa[i] = i;
23     for (int i = 1; i < n; i++) {
24         int u = a[i];
25         flag[u] = 1, total[u] = value[u];
26         mx = max(mx, total[u]);
27         for (int v : to[u]) {
28             if (!flag[v])
29                 continue;
30             int x = find(v), y = u;
31             if (x != y) {
32                 fa[x] = y;
33                 total[y] += total[x];
34                 mx = max(mx, total[y]);
35             }
36         }
37         ans.push_back(mx);
38     }
39     reverse(ans.begin(), ans.end());
40     for (long long answer : ans) cout << answer << " ";
41 }

T4：刮彩票(lottery)

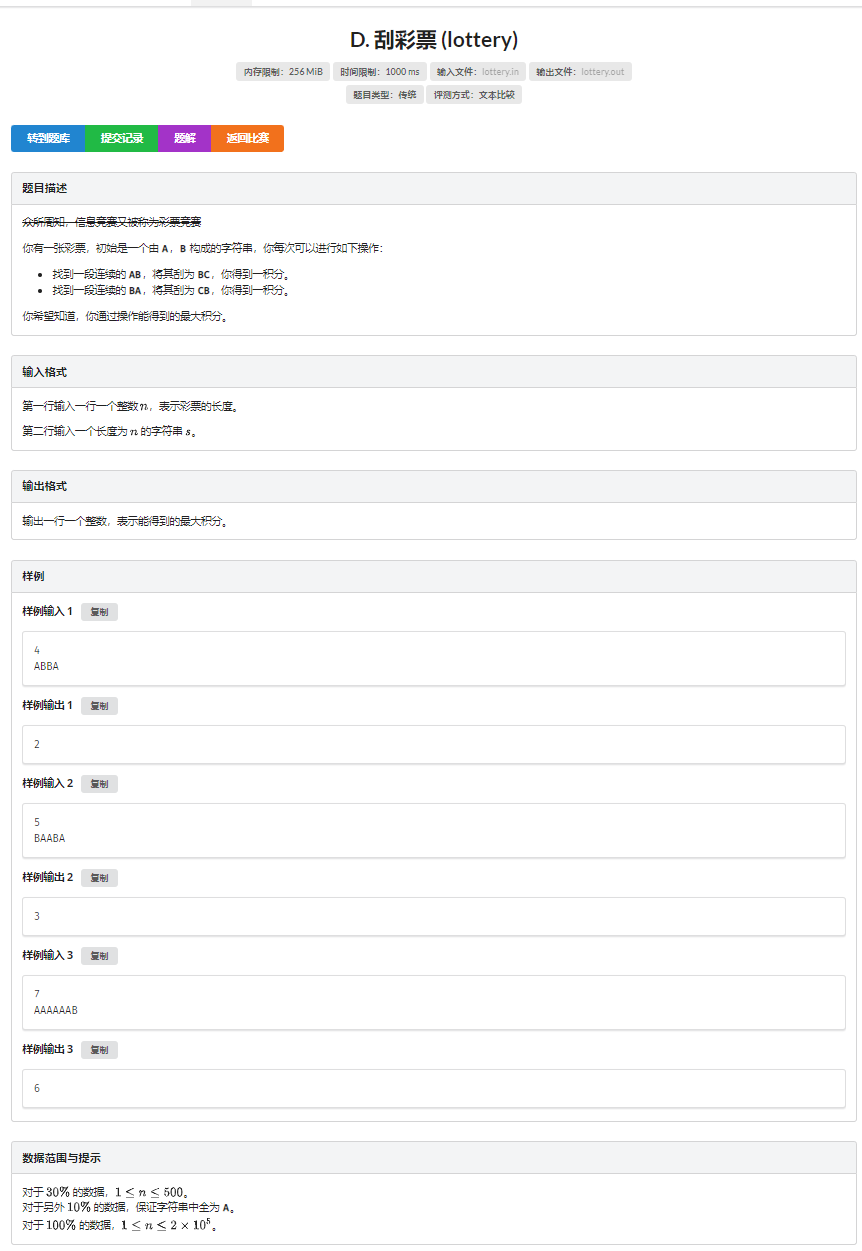
赛场上状态转移方程没想清楚，70pts(￣▽￣)"，祭了

简单模拟发现，操作相当于可以把一个形如 AAA……AB 的转化为 BCC……CC ，或将形如 BAA……AA 的转化

为 CC……CCB ，等价于将一个 A 连续段与一个与其相邻的 B 删去。 

故我们可以进行 dp，对于每个初始是 B 的位置 ，f(i,0/1)为在 的前缀字符串中， 位置有/没有被前面

的 A 连续段占用。

f(i,0)=max(f(la,0)+i-la-1,f(la,1))

f(i,1)=max(f(la,0)+i-la-1,f(la,i)+i-la-1)

其中la 为上一个 B 的位置.

最终答案为max(f(las,0)+n-las,f(la,1))，las为最后一个 B 的位置。

AC CODE

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 const int N=2e5+10;
 4 int n,f[N][2];
 5 char s[N];
 6 int main(){
 7     freopen("lottery.in","r",stdin);
 8     freopen("lottery.out","w",stdout);
 9     scanf("%d%s",&n,s+1);
10     int la=0;
11     f[0][0]=-n;
12     for(int i=1;i<=n;++i)
13         if(s[i]=='B'){
14             f[i][0]=max(f[la][0]+i-la-1,f[la][1]);
15             f[i][1]=max(f[la][0],f[la][1])+i-la-1;
16             la=i;
17         }
18     printf("%d\n",max(f[la][0]+n-la,f[la][1]));
19     return 0;
20 }

总370pts

完结，撒花*★,°*:.☆(￣▽￣)/$:*.°★* 。