神经网络优化篇：详解指数加权平均的偏差修正（Bias correction in exponentially weighted averages）

指数加权平均的偏差修正

\({{v}_{t}}=\beta {{v}_{t-1}}+(1-\beta ){{\theta }_{t}}\)

在上一个博客中，这个（红色）曲线对应\(\beta\)的值为0.9，这个（绿色）曲线对应的\(\beta\)=0.98，如果执行写在这里的公式，在\(\beta\)等于0.98的时候，得到的并不是绿色曲线，而是紫色曲线，可以注意到紫色曲线的起点较低，来看看怎么处理。

计算移动平均数的时候，初始化\(v_{0} = 0\)，\(v_{1} = 0.98v_{0} +0.02\theta_{1}\)，但是\(v_{0} =0\)，所以这部分没有了（\(0.98v_{0}\)），所以\(v_{1} =0.02\theta_{1}\)，所以如果一天温度是40华氏度，那么\(v_{1} = 0.02\theta_{1} =0.02 \times 40 = 8\)，因此得到的值会小很多，所以第一天温度的估测不准。

\(v_{2} = 0.98v_{1} + 0.02\theta_{2}\)，如果代入\(v_{1}\)，然后相乘，所以\(v_{2}= 0.98 \times 0.02\theta_{1} + 0.02\theta_{2} = 0.0196\theta_{1} +0.02\theta_{2}\)，假设\(\theta_{1}\)和\(\theta_{2}\)都是正数，计算后\(v_{2}\)要远小于\(\theta_{1}\)和\(\theta_{2}\)，所以\(v_{2}\)不能很好估测出这一年前两天的温度。

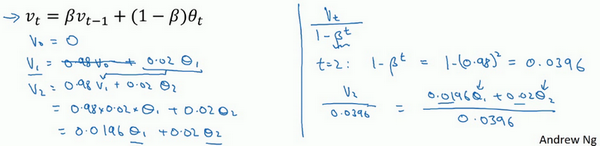
有个办法可以修改这一估测，让估测变得更好，更准确，特别是在估测初期，也就是不用\(v_{t}\)，而是用\(\frac{v_{t}}{1- \beta^{t}}\)，t就是现在的天数。举个具体例子，当\(t=2\)时，\(1 - \beta^{t} = 1 - {0.98}^{2} = 0.0396\)，因此对第二天温度的估测变成了\(\frac{v_{2}}{0.0396} =\frac{0.0196\theta_{1} + 0.02\theta_{2}}{0.0396}\)，也就是\(\theta_{1}\)和\(\theta_{2}\)的加权平均数，并去除了偏差。会发现随着\(t\)增加，\(\beta^{t}\)接近于0，所以当\(t\)很大的时候，偏差修正几乎没有作用，因此当\(t\)较大的时候，紫线基本和绿线重合了。不过在开始学习阶段，才开始预测热身练习，偏差修正可以帮助更好预测温度，偏差修正可以帮助使结果从紫线变成绿线。

在机器学习中，在计算指数加权平均数的大部分时候，大家不在乎执行偏差修正，因为大部分人宁愿熬过初始时期，拿到具有偏差的估测，然后继续计算下去。如果关心初始时期的偏差，在刚开始计算指数加权移动平均数的时候，偏差修正能帮助在早期获取更好的估测。