[SPOJ SEQN] [hdu3439]Sequence

题目就是求C(n,k)*H(n - k)%m

0<= k<= n <=10^9, 1 <= m <= 10^5, n != 0

其中H(n)是错排第n项。

对于C(n,k)%m可以参考我以前的文章

对于H(n)

直接套公式：

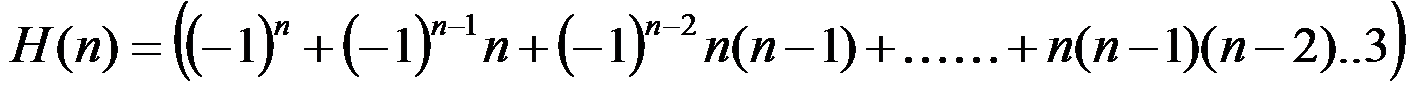
可以发现肯定在某一位会出现后面都是模完都是0

#include <cstdio>
#include <map>
using std::pair;
#define Pair pair<long long,long long>
const long long M = 100000 + 9;
long long fac[M],a[100],r[100];
struct triple{long long x,y,z;triple(const long long _x,const long long _y,const long long _z):x(_x),y(_y),z(_z){}};
triple exgcd(const long long a,const long long b)
{
    if (!b) return triple(1,0,a);
    triple last(exgcd(b,a%b));
    return triple(last.y,last.x - a/b * last.y,last.z);
}
long long CRT(const long long (&a)[100],const long long (&r)[100],const long long cnt)
{
    long long res = 0,MM = 1;
    for (long long i = 1; i <= cnt; ++i) MM *= a[i];
    for (long long i = 1; i <= cnt; ++i)
        (res += exgcd(MM / a[i],a[i]).x % a[i] * r[i] % MM * (MM / a[i]) % MM) %= MM;
    //printf("CRT %I64d\n",res + MM);
    return (res + MM) % MM;
}
long long power(long long n,long long k,long long MOD)
{
    n %= MOD;
    long long res = 1;
    for (; k; n = n * n % MOD,k /= 2)
        if (k & 1) res = res * n % MOD;
    return res;
}
long long H(const long long n,const long long MOD)
{
    //H(n) = (3 * ... * n) - (4 * ... * n) + (5 * ... * n) + ... + (-1)^(n-1) * n + (-1)^n
    if (n == 0) return 1 % MOD;
    if (n == 1) return 0;
    long long res = (n%2)?(-1):1;
    for (long long i = n,t = res; i >= 3; --i) {
        if (i % MOD == 0) break;
        (t = - t * i) %= MOD;
        (res += t) %= MOD;
    }
    //printf("TEST: %I64d\n",res + MOD);
    return (res + MOD) % MOD;
}
Pair FnModP(long long n,const long long p,const long long MOD)
{
    //Fn = n!
    //fac[n] = n! % p
    long long res = 1; long long c = 0;
    while (n) {
        (res *= power(fac[MOD],n / MOD,MOD)) %= MOD;
        (res *= fac[n % MOD]) %= MOD;
        n /= p;
        c += n;
    }
    return std::make_pair(c,res);
}
void calc_fac(const long long p,const long long MOD)
{
    fac[0] = 1;
    for (long long i = 1; i <= MOD; ++i)
        if (i % p) fac[i] = fac[i - 1] * i % MOD;
        else fac[i] = fac[i - 1];
}
long long C(const long long n,const long long K,const long long p,const long long MOD)
{
    //nCK % p^c
    calc_fac(p,MOD);
    Pair a(FnModP(n,p,MOD)),b(FnModP(K,p,MOD)),c(FnModP(n - K,p,MOD));
    return 1ll * power(p,a.first - b.first - c.first,MOD) * a.second % MOD * ((exgcd(1ll * b.second * c.second % MOD,MOD).x % MOD + MOD) % MOD) % MOD;
}
long long work(long long n,long long K,long long MOD)
{
    long long cnt = 0,c = 0;
    const long long m = MOD;
    for (long long i = 2; i * i <= MOD; ++i)
        if (MOD % i == 0) {
            a[++cnt] = 1;
            for (c = 0; MOD % i == 0; MOD /= i) ++c,a[cnt] *= i;
            r[cnt] = C(n,K,i,a[cnt]);
        }
    if (MOD > 1) r[++cnt] = C(n,K,MOD,MOD),a[cnt] = MOD;
    //for (long long i = 1; i <= cnt; ++i) printf("%I64d %I64d\n",a[i],r[i]);
    return 1ll * CRT(a,r,cnt) * H(n - K,m) % m;
}
int main()
{
    #ifndef ONLINE_JUDGE
    freopen("SEQN.in","r",stdin);
    freopen("SEQN.out","w",stdout);
    #endif
    long long T,n,K,MOD;
    scanf("%I64d",&T);
    for (long long i = 1; i <= T; ++i) {
        scanf("%I64d%I64d%I64d",&n,&K,&MOD);
        printf("Case %I64d: %I64d\n",i,(work(n,K,MOD)%MOD + MOD)%MOD);
    }
}