SPOJ FFT TSUM

第一道FFT的题目。

在网上找了很多FFT的资料，但一直都看不懂，最后是看算法导论学的FFT，算法导论上面写的很详细，每一步推导过程都有严格的证明。

下面说这道题

题意：

给一个序列s，有n个不互相同的整数。现在从这个序列中选出一个包含3个不同的整数的集合，对于他们的和为sum来说，求一共有多少种选法。(注意：3个数的先后顺序都看做一种选法)

分析：

构造一个多项式A(x)，这n个数作为多项式的指数。

A³(x)中的每一项的指数对应三个数的和，前面的系数是取数的方案数。

然而这并不是题目所求，这样的选法是任意取三个数，可能相同可能不同。

其中多计算了不合法的方案：

任意取三个数的方案数 = 取三个相同的数 + 取两个相同的数和另一个不同的数 + 三个互不相同的数

用式子表达出来就是： (图片来自叉姐PPT)

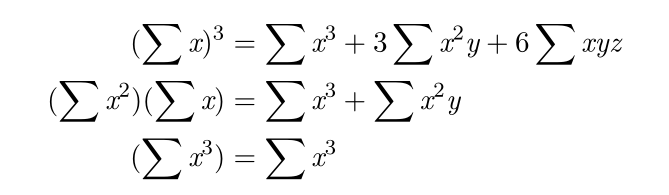
整理一下，答案就是：

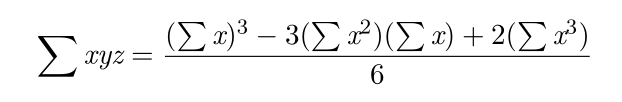
 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 #include <complex>
 #include <cmath>
 using namespace std;

 typedef long long LL;
 const double PI = acos(-1.0);
 typedef complex<double> Complex;

 const int maxn = ( << );

 void FFT(Complex P[], int n, int oper)
 {
     for(int i = , j = ; i < n - ; i++)
     {
         for(int s = n; j ^= s >>= , ~j & s; );
         if(i < j) swap(P[i], P[j]);
     }

     int log = ;
     while((n & ( << log)) == ) log++;
     for(int s = ; s < log; s++)
     {
         int m = ( << s);
         int m2 = m * ;
         Complex wm = Complex(cos(PI / m), sin(PI / m) * oper);
         for(int k = ; k < n; k += m2)
         {
             Complex w(, );
             for(int j = ; j < m; j++, w = w * wm)
             {
                 Complex t = w * P[k + j + m];
                 Complex u = P[k + j];
                 P[k + j] = u + t;
                 P[k + j + m] = u - t;
             }
         }
     }

     if(oper == -) for(int i = ; i < n; i++) P[i].real() /= n;
 }

 int A[maxn], A2[maxn], A3[maxn];
 Complex a[maxn], b[maxn];

 int main()
 {
     int n; scanf("%d", &n);
     while(n--)
     {
         int x; scanf("%d", &x);
         x += ;
         A[x]++;
         A2[x*]++;
         A3[x*]++;
     }
     for(int i = ; i < maxn; i++) a[i] = A[i], b[i] = A2[i];

     FFT(a, maxn, );
     FFT(b, maxn, );
     for(int i = ; i < maxn; i++) a[i] = a[i] * (a[i] * a[i] - b[i] * 3.0);
     FFT(a, maxn, -);

     for(int i = ; i < maxn; i++)
     {
         LL ans = (LL)((a[i].real() + 0.5) + A3[i] * ) / ;
         if(ans > ) printf("%d : %lld\n", i - , ans);
     }

     return ;
 }

代码君