Codeforces 633F - The Chocolate Spree（树形 dp）

Codeforces 题目传送门 & 洛谷题目传送门

看来我这个蒟蒻现在也只配刷刷 *2600 左右的题了/dk

这里提供一个奇奇怪怪的大常数做法。

首先还是考虑分析“两条不相交路径”的性质。我们以 \(1\) 号点为根。记 \(subtree(u)\) 为 \(u\) 子树内点的集合，那么对于两条不相交的路径 \(P_1,P_2\)，下面两条一定有至少一条成立：

• \(\exist u\) 满足 \(\forall v\in P_1,v\in subtree(u),\forall v\in subtree(u),v\notin P_2\)
• \(\exist u\) 满足 \(\forall v\in P_2,v\in subtree(u),\forall v\in subtree(u),v\notin P_1\)

用人话说就是两条路径中一定存在一条路径满足另一条路径中任何一个点都不在其 LCA 的子树中。

我们不妨枚举这条路径的 LCA \(u\)，按照树的直径的套路我们求出 \(f_u\) 表示以 \(u\) 为链顶的链中，权值最大的链的权值之和；\(g_u\) 表示以 \(u\) 为链顶的链中权值第二大的，并且链向下延伸到的儿子与 \(f_u\) 表示的链向下延伸到的儿子不同的链的权值之和（可能讲的不是太清楚，不过学过树的直径的应该都知道是什么意思罢）。那么显然以 \(u\) 为 LCA 的链权值之和的最大值就是 \(f_u+g_u-a_u\)。

故现在我们的任务就是求出另一条链长度的最大值，也就是抠掉 \(u\) 的子树后剩余部分的直径长度，这个东西怎么求呢？

我们考虑将剩余部分以 \(fa_u\) 为根，其中 \(fa_i\) 为 \(i\) 在原树中的父亲。

还是套路地枚举第二条路径在剩余子树部分中的 LCA \(v\)，记 \(f'_u\) 为在新的树中以 \(u\) 为链顶的链中，权值最大的链的权值之和；\(g'_u\) 表示以 \(u\) 为链顶的链中权值第二大的，并且链向下延伸到的儿子与 \(g'_u\) 表示的链向下延伸到的儿子不同的链的权值之和。那么这部分对答案的贡献应当为 \(f_u+g_u-a_u+\max\{f'_v+g'_v-a_v\}\)。

但是显然我们每次枚举 \(u\) 都重新求一遍 \(f'_u,g'_u\) 是不现实的，我们不妨来探究一下 \(f'_u,g'_u\) 究竟与 \(f_u,g_u\) 有什么关系。

比方说有如下图所示的树：

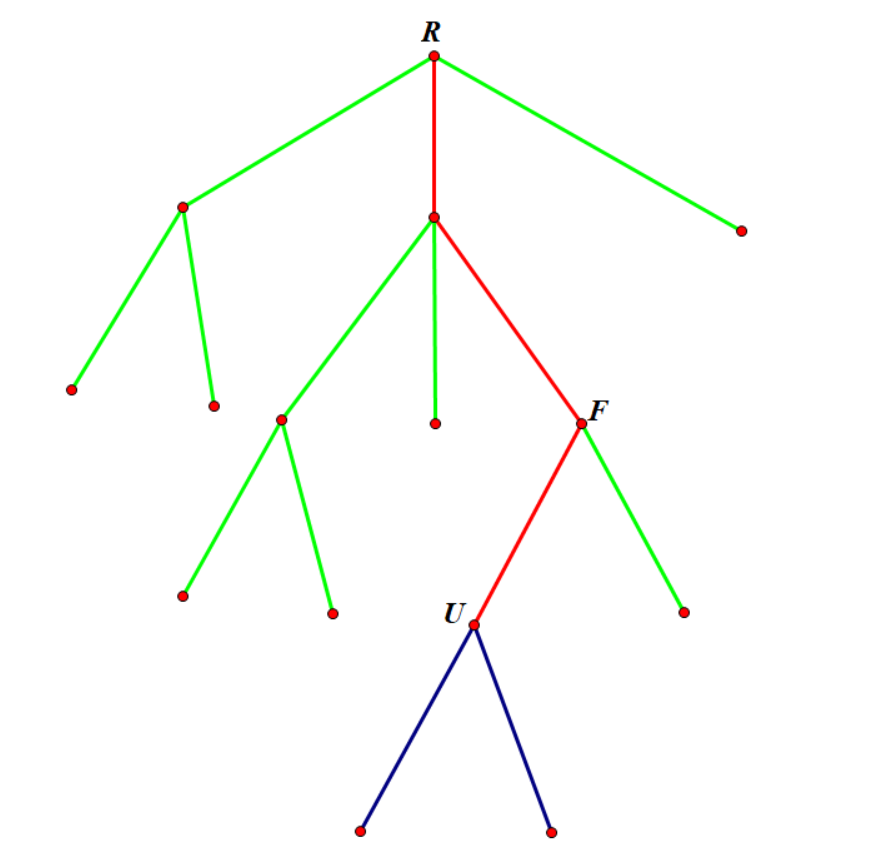
假设我们枚举到了点 \(U\)，原树的根为 \(R\)。我们抠掉 \(U\) 的子树部分之后以 \(F\) 为根，剩余部分长这样：

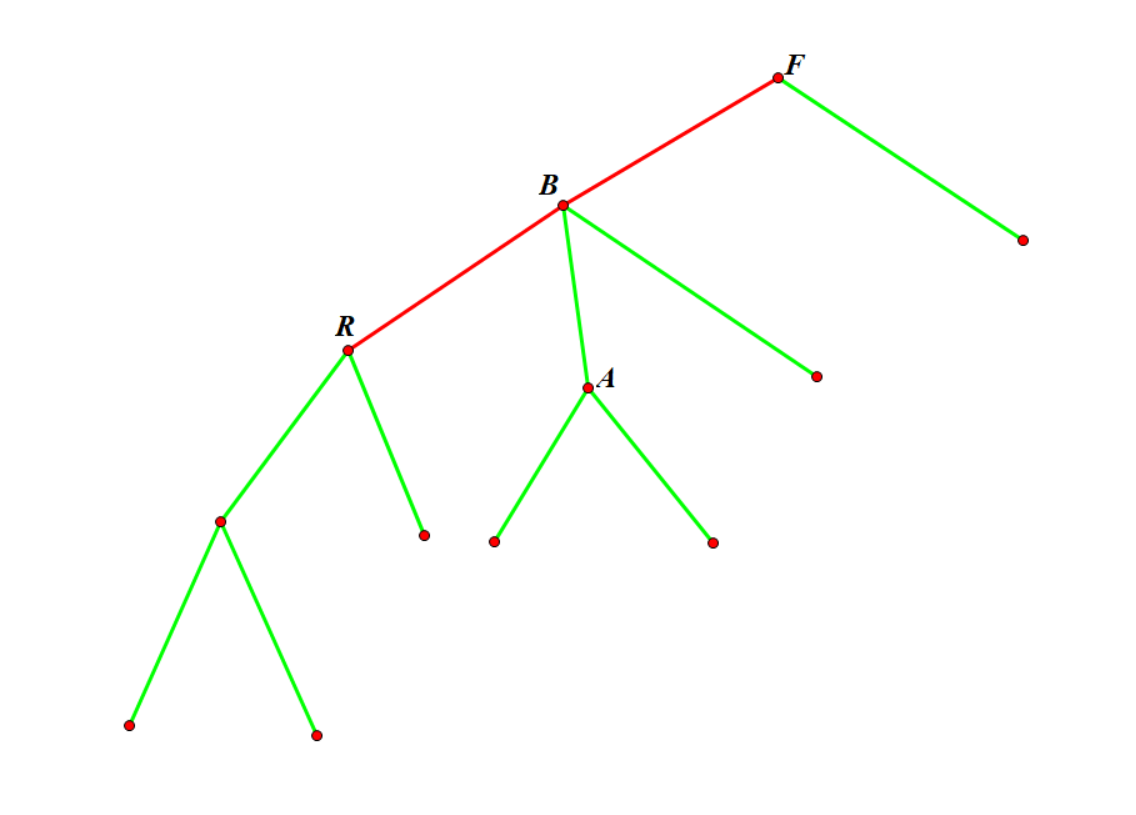
考虑将剩余的子树中的节点 \(v\) 分为两类：

1. \(v\) 不在 \(u\) 到根节点的路径上，譬如图中的 \(A\) 点，很容易注意到的一点是新树中 \(A\) 子树内的点集与原树中 \(A\) 子树内的点集相同，故对于这样的点 \(v\) 一定有 \(f'_v=f_v,g'_v=g_v\)。而显然点 \(v\) 满足该条件当且仅当 \(v\) 与 \(u\) 不存在祖先关系。如果我们记 \(h_u=f_u+g_u-a_u\)，那么这部分的贡献应为 \(h_u+h_v\)。故所有这样的点对 \((u,v)\) 所能产生的最大贡献就是 \(\max\limits_{u,v\ \text{不存在祖先关系}}h_u+h_v\)，考虑枚举 \(w=\text{LCA}(u,v)\)，记 \(mx_u=\max\limits_{v\in subtree(u)}h_v\)，那么以 \(w\) 为 LCA 的 \(u,v\) 产生的贡献的最大值就是 \(\max\limits_{u,v\in son(w),u\ne v}mx_u+mx_v\)，这个显然可以一遍 DFS 搞定，在 DFS 过程中记录最小值和次小值即可。
2. \(v\) 在 \(u\) 到根节点的路径上，譬如图中的 \(B\) 点，对于这样点 \(v\)，也有 \(u\) 在新子树内的点集就是 \(\{1,2,\dots,n\}\) 扣掉原树内 \(v\) 在 \(u\) 方向的儿子的子树内的点集。我们记 \(of_v\) 为扣掉 \(v\) 的子树内的后，以 \(fa_v\) 为根后，以 \(v\) 为链顶的链的权值的最大值，\(og_v\) 仿照前文也有类似的定义。那么 \(f'_v=of_s,g'_v=og_s\)，其中 \(s\) 为 \(v\) 在 \(u\) 方向的儿子。考虑一遍 DFS 用换根 dp 的套路求出 \(of_u,og_u\)，那么这部分贡献的最大值就是 \(f_u+g_u-a_u+\max\limits_{v\ \text{为}\ u\ \text{的祖先},v\ne 1}\{of_v+og_v-a_v\}\)，这个又可以一遍 DFS 求出。

时间复杂度 \(\mathcal O(n)\)，总共需四遍 DFS，第一遍 DFS 求出 \(f_i,g_i\)，第二遍 DFS 用换根 dp 的套路求出 \(of_i,og_i\)，第三遍 DFS 求出 \(\max\limits_{u,v\ \text{不存在祖先关系}}h_u+h_v\)，第四遍 DFS 求出 \(\max f_u+g_u-a_u+\max\limits_{v\ \text{为}\ u\ \text{的祖先},v\ne 1}\{of_v+og_v-a_v\}\)。常数较大，跑得最慢的一个点跑了 171ms。

代码如下（代码中 dfs1,dfs2,dfs3,dfs4 分别对应上文中提到的四遍 DFS）：

#include <bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define fill0(a) memset(a,0,sizeof(a))
#define fill1(a) memset(a,-1,sizeof(a))
#define fillbig(a) memset(a,63,sizeof(a))
#define pb push_back
#define ppb pop_back
#define mp make_pair
template<typename T1,typename T2> void chkmin(T1 &x,T2 y){if(x>y) x=y;}
template<typename T1,typename T2> void chkmax(T1 &x,T2 y){if(x<y) x=y;}
typedef pair<int,int> pii;
typedef long long ll;
typedef unsigned int u32;
typedef unsigned long long u64;
namespace fastio{
	#define FILE_SIZE 1<<23
	char rbuf[FILE_SIZE],*p1=rbuf,*p2=rbuf,wbuf[FILE_SIZE],*p3=wbuf;
	inline char getc(){return p1==p2&&(p2=(p1=rbuf)+fread(rbuf,1,FILE_SIZE,stdin),p1==p2)?-1:*p1++;}
	inline void putc(char x){(*p3++=x);}
	template<typename T> void read(T &x){
		x=0;char c=getchar();T neg=0;
		while(!isdigit(c)) neg|=!(c^'-'),c=getchar();
		while(isdigit(c)) x=(x<<3)+(x<<1)+(c^48),c=getchar();
		if(neg) x=(~x)+1;
	}
	template<typename T> void recursive_print(T x){if(!x) return;recursive_print(x/10);putc(x%10^48);}
	template<typename T> void print(T x){if(!x) putc('0');if(x<0) putc('-'),x=~x+1;recursive_print(x);}
	void print_final(){fwrite(wbuf,1,p3-wbuf,stdout);}
}
const int MAXN=1e5;
int n,a[MAXN+5];
vector<int> g[MAXN+5];
vector<pair<ll,ll> > pre[MAXN+5];
vector<pair<ll,ll> > suf[MAXN+5];
pair<ll,ll> out[MAXN+5],dp[MAXN+5];
pair<ll,ll> merge(pair<ll,ll> x,ll y){
	ll a[3]={0};a[0]=x.fi;a[1]=x.se;a[2]=y;
	sort(a,a+3);reverse(a,a+3);return mp(a[0],a[1]);
}
void dfs1(int x=1,int f=0){
	for(int i=0;i<g[x].size();i++){
		int y=g[x][i];if(y==f) continue;
		dfs1(y,x);dp[x]=merge(dp[x],dp[y].fi+a[y]);
	}
}
void dfs2(int x=1,int f=0){
	pre[x].resize(g[x].size()+2);
	suf[x].resize(g[x].size()+2);
	for(int i=0;i<g[x].size();i++){
		int y=g[x][i];
		if(y==f) pre[x][i+1]=merge(pre[x][i],out[x].fi+a[f]);
		else pre[x][i+1]=merge(pre[x][i],dp[y].fi+a[y]);
	}
	for(int i=(int)g[x].size()-1;~i;i--){
		int y=g[x][i];
		if(y==f) suf[x][i+1]=merge(suf[x][i+2],out[x].fi+a[f]);
		else suf[x][i+1]=merge(suf[x][i+2],dp[y].fi+a[y]);
	}
	for(int i=0;i<g[x].size();i++){
		int y=g[x][i];if(y==f) continue;
		ll a[4]={0};
		a[0]=pre[x][i].fi;a[1]=pre[x][i].se;
		a[2]=suf[x][i+2].fi;a[3]=suf[x][i+2].se;
		sort(a,a+4);reverse(a,a+4);out[y]=mp(a[0],a[1]);
		dfs2(y,x);
	}
}
ll mx[MAXN+5],ans=0;
void dfs3(int x=1,int f=0){
	mx[x]=dp[x].fi+dp[x].se+a[x];
	ll mx1=0,mx2=0;
	for(int i=0;i<g[x].size();i++){
		int y=g[x][i];if(y==f) continue;
		dfs3(y,x);chkmax(mx[x],mx[y]);
		if(mx[y]>mx1) mx2=mx1,mx1=mx[y];
		else if(mx[y]>mx2) mx2=mx[y];
	}
	if(mx2) chkmax(ans,mx1+mx2);
}
ll mxx[MAXN+5];
void dfs4(int x=1,int f=0){
	if(x!=1) chkmax(ans,dp[x].fi+dp[x].se+a[x]+mxx[x]);
	for(int i=0;i<g[x].size();i++){
		int y=g[x][i];if(y==f) continue;
		mxx[y]=max(mxx[x],out[y].fi+out[y].se+a[x]);dfs4(y,x);
	}
}
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	for(int i=1,u,v;i<n;i++) scanf("%d%d",&u,&v),g[u].pb(v),g[v].pb(u);
	dfs1();dfs2();dfs3();dfs4();printf("%lld\n",ans);
	return 0;
}
/*1
9
1 2 3 4 5 6 7 8 9
1 2
1 3
1 4
1 5
1 6
1 7
1 8
1 9
*/
/*2
2
20 10
1 2
*/
/*
5
1 5 4 2 3
1 2
2 3
2 4
1 5
*/