hdu1852 Beijing 2008

题目链接：

http://acm.hdu.edu.cn/showproblem.php?pid=1852

题目大意：

求2008^n的所有因子和m对k取余，然后求2008^m对k取余。

解题思路：

首先将2008因式分解，2008 = 2^3 * 251

所以2008^n = 2^(3n) * 251^(n)

因子和m =（2^(3n+1）- 1) * （251^(n+1) - 1）/ 250

m需要对k取余数。由于余数k和250可能不互质，也就是没有逆元存在，那么需要用到通用公式：

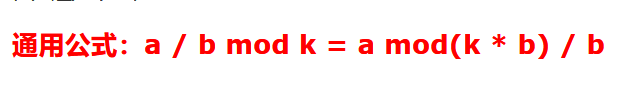
所以可以用快速幂求出（2^(3n+1）- 1) mod k

再求出（251^(n+1) - 1）mod (250 * k) / 250

两者相乘再对k求余数作为2008的指数

最后快速幂求出答案

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 ll pow(ll a, ll b, ll m)
 {
     ll ans = ;
     a %= m;
     while(b)
     {
         if(b & )ans = ans * a % m;
         b /= ;
         a *= a;
         a %= m;
     }
     return ans;
 }
 int main()
 {
     ll n, k;
     while(cin >> n >> k && n)
     {
         ll a = pow(,  * n + , k) - ;
         ll b = (pow(, n + ,  * k) - ) % ( * k);
         b /= ;
         cout<<pow(, (a * b) % k, k)<<endl;//此处必须a*b需要先对k取余数，题目求的是因子和m对k取余数作为指数的值
     }
     return ;
 }