sgu 101 domino

题意还算简洁明了，加上有道翻译凑过着读完了题。题意大体上是 给你 n 个多米诺骨牌， 给出每个骨牌两端的数字， 只有数字相同才可以推到， 比如 2-3和3-2。你可以旋转这些多米诺骨牌， 输出一个可以全部推到的方案， 如果没有 ，输出 No solution。

第一眼看上去像爆搜， 但是 n 最大到100， 时限竟然只有0.25s，铁定超时， 换个思路， 想不出来， 看了题解，才发现原来是图论题，我们把 0~6 当做点，把每个骨牌当做边， 这样构成了一个图， 我们需要求得就是 遍历所有的边且不重复。

这个可以算是一个 欧拉路 模板题，注意，是 欧拉路， 不是欧拉回路 ，被坑了好久。

欧拉路和欧拉回路都是一笔画问题， 两者都需要满足一个必要条件 ： 度数为奇数的要么没有， 要么有2个。 度数就是这个点连得边的条数。

先说欧拉回路， 欧拉回路由于需要回到原点， 所以一定没有度数为奇的点， 只要从任意一点 dfs ，走过的边不再走， 直到无边可走， 就是欧拉回路，此时一定是在原点。

但是，欧拉路不同， 欧拉路可以不回到原点， 这导致 dfs 有可能导致死胡同 ， 看一个例子 ：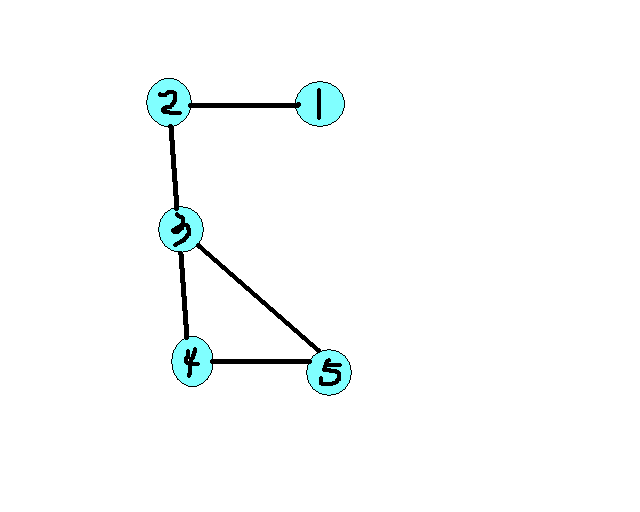

在这个例子里， 如果从 3 开始 dfs, 我们有可能回走到 2 ，然后走到 1， 这时我们发现无路可走了， 但这本应是一个一笔画， 只要从 1 出发就可以了，但是我们在程序里不好判断从哪个点开始， 所以， 引入欧拉路的求法：

从任意一个度数为奇的点开始，仍然 dfs，但是 我们不一开始就把这个点加入答案， 而是先任选和这个点相连的一条边， 继续向下dfs， 然后在把这个店加入答案，就等于是倒序输出。这样很巧妙的解决了上面说的问题。光这么说可能不太好理解，一看代码立刻就能明白。

void ss(int now)
{
    遍历每一条和这个点相连的边
    {
        标记已经走过这条边，以后不再走
                ss(和它相邻的点);
        把现在这个点加入答案
    }
}

如此一来就可以了， 但要注意，要判断此图是否联通， 只需判断你求出的边数和骨牌数是否相等就行了，上代码：

#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <iostream>
#include <algorithm>
#define N 110 * 2
#define M 10
using namespace std;

int n, du[M] = {};
int p[M], next[N*], v[N*], zheng[N*], bnum = -, kexing[N*], num[N*];
int ans[N][], ansnum = ;

void addbian(int x, int y, int now)
{
    bnum++; next[bnum] = p[x]; p[x] = bnum;
    v[bnum] = y; zheng[bnum] = ; kexing[bnum] = ; num[bnum] = now;
    bnum++; next[bnum] = p[y]; p[y] = bnum;
    v[bnum] = x; zheng[bnum] = ; kexing[bnum] = ; num[bnum] = now;
}

void ss(int now)
{
    int k = p[now];
    while (k != -)
    {
        if (kexing[k])
        {
            kexing[k] = ; kexing[k^] = ;
            ss(v[k]);
            ansnum++;
            ans[ansnum][] = num[k^];
            ans[ansnum][] = zheng[k^];
        }
        k = next[k];
    }
}

int main()
{
    scanf("%d", &n);
    for (int i = ; i <= ; ++i) p[i] = -;
    for (int i = ; i <= n; ++i)
    {
        int x, y;
        scanf("%d%d", &x, &y);
        du[x]++; du[y]++;
        addbian(x, y, i);
    }
    if (n == )
    {
        printf("No solution\n");
        return ;
    }
    int jnum = , start = -;
    for (int i = ; i <= ; ++i)
        if (du[i] %  != )
        {
            jnum++; start = i;
        }
    if (jnum != && jnum != )
    {
        printf("No solution\n");
        return ;
    }
    if (start == -)
        for (int i = ; i <= ; ++i)
            if (du[i] != ) start = i;
    ss(start);
    if (ansnum < n)
    {
        printf("No solution\n");
        return ;
    }
    for (int i = ; i <= n; ++i)
    {
        printf("%d ",ans[i][]);
        if (ans[i][]) printf("+\n");
        else printf("-\n");
    }
}