个人实战演练全过程——No.1 最大连续子数组求和

之前的一次个人总结和一次单元测试入门学习是开启软件工程课程的前奏曲，也是热身，现在大家对于这门课程也有了初步的了解和认识，这次要开始真正的演奏了，要从头到尾完全靠自己的能力来解决一个问题，进行实战演练了。以下就是这次实战的全过程。

阅读目录

题目及要求

由于本次作业题为二选一，我选择了题目一。

题目一：最大连续子数组和（最大子段和）

问题： 给定n个整数（可能为负数）组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0，依此定义，所求的最优值为： Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n
例如，当（a[1],a[2],a[3],a[4],a[5],a[6]）=(-2,11,-4,13,-5,-2)时，最大子段和为20。

要求：

(1) 请从上述两个题目中根据个人实力任选一题，要求写出可运行的完整代码提交至GitHub或者Coding.net系统中，并将代码地址附到博客内。

(2) 请从语句覆盖、判定覆盖、条件覆盖、判定/条件覆盖、条件组合覆盖五个覆盖标准中（条件组合覆盖难度较大，鼓励尝试，但请谨慎选择），任选一个标准设计测试用例。

(3) 请利用自动测试工具对程序进行测试。

(4) 请将程序运行结果和自动测试分析结果截图附到博客中。

设计思路

看完这个题目之后，觉得特别的眼熟，记得以前学习算法与数据结构的时候对这个题就有一些印象，但是当时没有仔细做。题目要求不仅要编出可运行的程序，提交到Coding.net系统中，还要从语句覆盖、判定覆盖、条件覆盖、判定/条件覆盖、条件组合覆盖这五个覆盖标准中选择一个标准来设计测试用例，并用自动测试工具检测，这里结合了写上一篇博客时学到的单元测试的方法。

本题我的解题思路是：
只管当前连续子数组的和。设置一个thissum变量来计算当前连续子数组的和，再用一个sum变量来与当前变量thissum相比较，如果thissum>sum，就将sum赋值为thissum。如果不小于，那么就要判断thissum是否小于0，如果是，那么无论后面再加上什么数字都会让子数组变得更小，所以就要抛弃当前子数组，重新开始计算子数组的值。

另外，题目中有说明如果所有整数都为负数则定义子段和为0，在我设计的这个方法中就不需要去额外判断每一个值都是否为负数，因为在最开始就定义了sum为0，只有当前thissum>0时sum值才会改变，全负数的时候sum值是不会改变的。

PSP2.1表格

PSP2.1	PSP阶段	预估耗时（分钟）	实际耗时（分钟）
Planning	计划	10	15
· Estimate	· 估计这个任务需要多少时间	10	15
Development	开发	295	370
· Analysis	· 需求分析 (包括学习新技术)	45	50
· Design Spec	· 生成设计文档	10	15
· Design Review	· 设计复审	10	10
· Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	10	10
· Design	· 具体设计	30	35
· Coding	· 具体编码	30	40
· Code Review	· 代码复审	10	10
· Test	· 测试（自我测试，修改代码，提交修改）	60	80
Reporting	报告	60	80
· Test Report	· 测试报告	50	65
· Size Measurement	· 计算工作量	10	10
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	30	30
Summary	合计	325	405

实现过程

第一次使用vs2017来进行项目的创建，有些功能的使用还不是很熟练，但是经过自学还是可以很快上手的。

在上传至coding的时候也遇到了一些疑惑，因为想要下载安装Git，使用它来进行上传。附简单教程以及coding使用常见问题

本题代码链接：https://coding.net/u/mingmoushanlai/p/MAXarrayproject/git?public=true

执行测试样例截图：

覆盖标准

上一篇博客我了解单元测试的好处：

提高开发速度——可以以自动化方式执行的，提升了测试代码的执行效率。
提高软件代码质量——它使用小版本发布至集成，便于实现人员除错。同时引入重构概念，让代码更干净和富有弹性。
提升系统的可信赖度——它是回归测试的一种。支持修复或更正后的“再测试”，可确保代码的正确性

这次在课上了解到了白盒测试法。白盒法以程序（模块）内部的逻辑结构为基础来设计测试用例，主要用于单元测试。白盒法又称为逻辑覆盖法，其测试用例选择，是按照不同覆盖标准确定的。

白盒测试法的步骤

选择逻辑覆盖标准。
按照覆盖标准列出所有情况。
选择确定测试用例。
验证分析运行结果与预期结果。

这里有五个不同的覆盖标准

1.语句覆盖： 是最起码的结构覆盖要求，选择足够的测试用例，使得程序中每个语句至少都能被执行一次。
优点：以很直观地从源代码得到测试用例，无须细分每条判定表达式。
缺点：这种测试方法仅仅针对程序逻辑中显式存在的语句，但对于隐藏的条件和可能到达的隐式逻辑分支，是无法测试的。

2.判定覆盖： 执行足够的测试用例，使得程序中每个判定至少都获得一次“真”值和“假”值。即：程序中的每个分支至少执行一次。每个判断的取真、取假至少执行一次。
优点：判定覆盖比语句覆盖要多几乎一倍的测试路径，当然也就具有比语句覆盖更强的测试能力。同样判定覆盖也具有和语句覆盖一样的简单性，无须细分每个判定就可以得到测试用例。
缺点：往往大部分的判定语句是由多个逻辑条件组合而成，若仅仅判断其整个最终结果，而忽略每个条件的取值情况，必然会遗漏部分测试路径。

3.条件覆盖：执行足够的测试用例，使得判定中的每个条件获得各种可能的结果。即每个条件至少有一次为真值，有一次为假值。
优点：条件覆盖比判定覆盖，增加了对符合判定情况的测试，增加了测试路径。
缺点：要达到条件覆盖，需要足够多的测试用例，但条件覆盖并不能保证判定覆盖。条件覆盖只能保证每个条件至少有一次为真，而不考虑所有的判定结果。

4.判定/条件覆盖： 执行足够的测试用例，使得判定中每个条件取到各种可能的值，并使每个判定取到各种可能的结果。
优点：判定/条件覆盖满足判定覆盖准则和条件覆盖准则，弥补了二者的不足。
缺点：判定/条件覆盖准则的缺点是未考虑条件的组合情况。

5.条件组合覆盖： 执行足够的例子，使得每个判定中条件的各种可能组合都至少出现一次。
优点：多重条件覆盖准则满足判定覆盖、条件覆盖和判定/条件覆盖准则。更改的判定/条件覆盖要求设计足够多的测试用例，使得判定中每个条件的所有可能结果至少出现一次，每个判定本身的所有可能结果也至少出现一次。并且每个条件都显示能单独影响判定结果。
缺点：线性地增加了测试用例的数量。

在这里考虑到代码中的条件和判定，我选择了判定/条件覆盖标准来设计测试用例。

流程图及测试用例

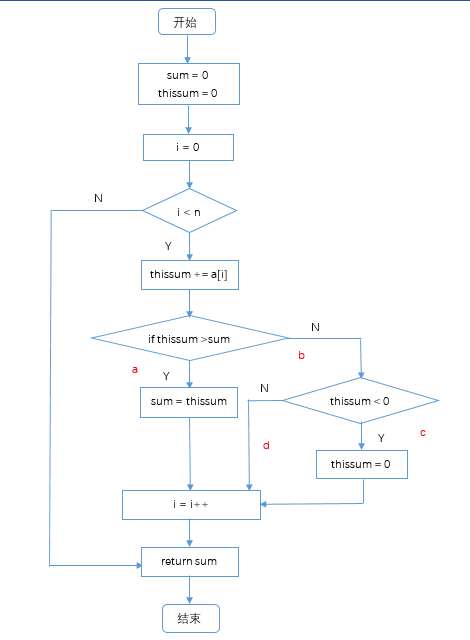
在本函数的流程图中，循环内部程序中的每个分支至少执行一次，共有四个分支，如上图中的a、b、c、d。且判定中的每个条件获得各种可能的结果有四种，分别为①thissum>sum ②thissum≤sum ③thissum≤0 ④thissum>0。我选择了判定/条件覆盖标准来设计测试用例，为使得判定中每个条件取到各种可能的值，并使每个判定取到各种可能的结果，选取的样例如下：
测试用例①
n=5 数组数据为-4 8 -3 2 2 在这个n为5的循环中每一种判定和条件所取得的可能都会实现。

测试用例②
当n=5 数组数据为-1 -2 -3 -4 -5 会出现数值全为负数的特殊情况。

测试结果如图所示：

总结与体会

个人实战练习比理论上的学习加大了难度，只有真正做这个练习的时候才知道它的艰难。个人开发技术对于一名软件工程师来说是十分重要的，在这个过程中能够衡量个人能力，我们也需要通过这次实战演练来明确学习一些主流软件开发工具的安装和使用过程，也要能够利用相关的方法分析软件的效能，用自动检测技术进行单元测试。

在自己进行这个题目的时候还是需要自己查询和解决许多问题，算法问题、新工具使用问题、测试问题。每解决一个问题就多了一份自信，也多了一份想要继续学习的好奇心。希望每一次写的博客都能给自己带来一些学习的动力和兴趣，希望每一次写的博客都能够记录自己在这段小时间内学习的成果，希望每一次都能够用心去对待每一篇，给未来的自己更多坚持下去的决心。

理论所不能解决的那些疑难，实践会给你解决。———— 费尔巴哈