BZOJ5300 [Cqoi2018]九连环 【数学】【FFT】

题目分析：

　　这道题是数学必修五的原题，做法如下图，书上讲得很详细了。

　　

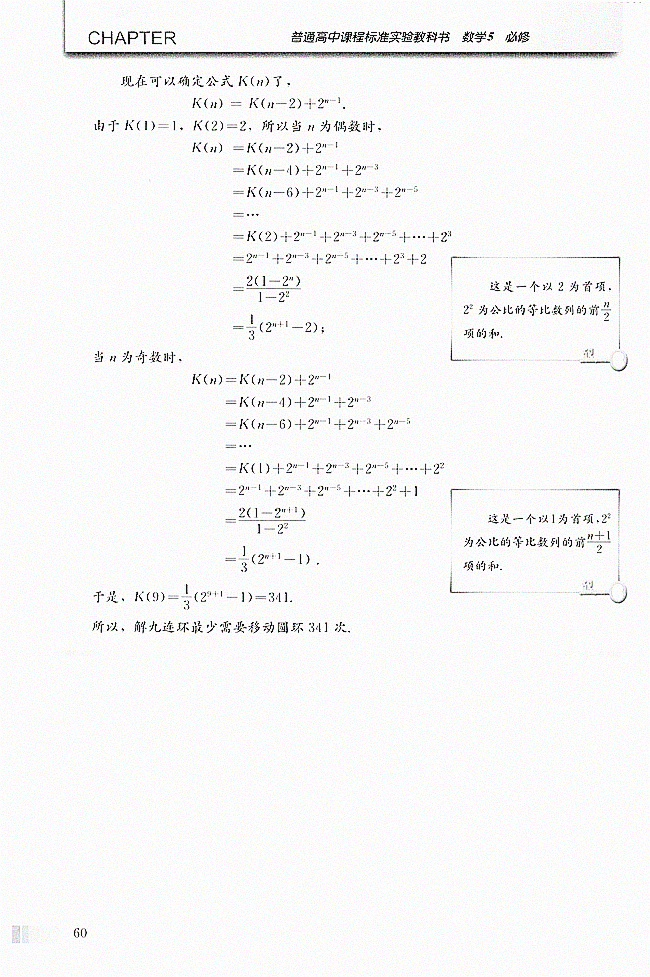
那么这道题目用快速幂就可以解决了，值得注意的是，分析时间复杂度会发现直接做乘法其实是O(n^2)的，但是有一个1/20左右的常数，可能可以卡进去。为了追求稳定，考虑采用FFT优化。

emm,,,FFT做这种题是大材小用吧，用python写吧，理由是python的乘法是用fft实现的。

代码：

t=input()
count=0
while(count<t):
    try:
       a=input()
       x=2**(a+1)
       if a % 2 == 0:
               x=x-2;
               x=x//3;
       else:
               x=x-1;
               x=x//3;
       print x
    except:
        break