逻辑回归&线性回归
# coding:utf-8
import numpy as np
from sklearn import linear_model, datasets
import matplotlib.pyplot as plt
from scipy.stats import norm
from scipy import fft
from scipy.io import wavfile
n = 40
# hstack数据拼接
# rvs是Random Variates随机变量的意思
# 在模拟X的时候使用了两个正态分布,分别制定各自的均值,方差,生成40个点
X = np.hstack((norm.rvs(loc=2, size=n, scale=2), norm.rvs(loc=8, size=n, scale=3)))
# zeros使得数据点生成40个0,ones使得数据点生成40个1
y = np.hstack((np.zeros(n), np.ones(n)))
# 创建一个 10 * 4 点(point)的图,并设置分辨率为 80
plt.figure(figsize=(10, 4), dpi=80)
# 设置横轴的上下限
plt.xlim((-5, 20))
# scatter散点图
plt.scatter(X, y, c=y)
plt.xlabel("feature value")
plt.ylabel("class")
plt.grid(True, linestyle='-', color='0.75')
plt.savefig("C:/Users/zhen/Desktop/logistic_classify.png", bbox_inches="tight")
# linspace是在-5到15的区间内找10个数
xs = np.linspace(-5, 15, 10)
# ---linear regression----------
from sklearn.linear_model import LinearRegression
clf = LinearRegression()
# reshape重新把array变成了80行1列二维数组,符合机器学习多维线性回归格式
clf.fit(X.reshape(n * 2, 1), y)
def lin_model(clf, X):
return clf.intercept_ + clf.coef_ * X
# --logistic regression--------
from sklearn.linear_model import LogisticRegression
logclf = LogisticRegression()
# reshape重新把array变成了80行1列二维数组,符合机器学习多维线性回归格式
logclf.fit(X.reshape(n * 2, 1), y)
def lr_model(clf, X):
return 1.0 / (1.0 + np.exp(-(clf.intercept_ + clf.coef_ * X)))
# ----plot---------------------------
plt.figure(figsize=(10, 5))
# 创建一个一行两列子图的图像中第一个图
plt.subplot(1, 2, 1)
plt.scatter(X, y, c=y)
plt.plot(X, lin_model(clf, X), "o", color="orange")
plt.plot(xs, lin_model(clf, xs), "-", color="green")
plt.xlabel("feature value")
plt.ylabel("class")
plt.title("linear fit")
plt.grid(True, linestyle='-', color='0.75')
# 创建一个一行两列子图的图像中第二个图
plt.subplot(1, 2, 2)
plt.scatter(X, y, c=y)
plt.plot(X, lr_model(logclf, X).ravel(), "o", color="c")
plt.plot(xs, lr_model(logclf, xs).ravel(), "-", color="green")
plt.xlabel("feature value")
plt.ylabel("class")
plt.title("logistic fit")
plt.grid(True, linestyle='-', color='0.75')
plt.tight_layout(pad=0.4, w_pad=0, h_pad=1.0)
plt.savefig("C:/Users/zhen/Desktop/logistic_classify2.png", bbox_inches="tight")
结果:
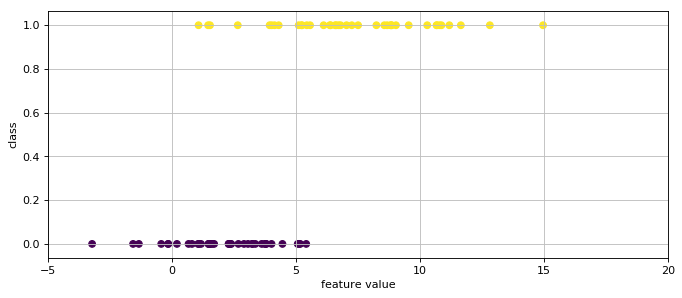

逻辑回归&线性回归的更多相关文章
- 02-12 Logistic(逻辑)回归
目录 逻辑回归 一.逻辑回归学习目标 二.逻辑回归引入 三.逻辑回归详解 3.1 线性回归与逻辑回归 3.2 二元逻辑回归的假设函数 3.2.1 让步比 3.2.2 Sigmoid函数图像 3.3 二 ...
- Matlab实现线性回归和逻辑回归: Linear Regression & Logistic Regression
原文:http://blog.csdn.net/abcjennifer/article/details/7732417 本文为Maching Learning 栏目补充内容,为上几章中所提到单参数线性 ...
- Machine Learning 学习笔记 (1) —— 线性回归与逻辑回归
本系列文章允许转载,转载请保留全文! [请先阅读][说明&总目录]http://www.cnblogs.com/tbcaaa8/p/4415055.html 1. 梯度下降法 (Gradien ...
- 【数据分析】线性回归与逻辑回归(R语言实现)
文章来源:公众号-智能化IT系统. 回归模型有多种,一般在数据分析中用的比较常用的有线性回归和逻辑回归.其描述的是一组因变量和自变量之间的关系,通过特定的方程来模拟.这么做的目的也是为了预测,但有时也 ...
- 线性回归,逻辑回归,神经网络,SVM的总结
目录 线性回归,逻辑回归,神经网络,SVM的总结 线性回归,逻辑回归,神经网络,SVM的总结 详细的学习笔记. markdown的公式编辑手册. 回归的含义: 回归就是指根据之前的数据预测一个准确的输 ...
- 【Coursera】线性回归和逻辑回归
一.线性回归 1.批量梯度下降法 每次对参数进行一次迭代时,都要扫描一遍输入全集 算法可以收敛到局部最优值 当迭代多次之后,每次迭代参数的改变越小 2.随机梯度下降法 对于一个输入样本,对参数进行一次 ...
- 线性回归,感知机,逻辑回归(GD,SGD)
线性回归 线性回归是一个回归问题,即用一条线去拟合训练数据 线性回归的模型: 通过训练数据学习一个特征的线性组合,以此作为预测函数. 训练目标:根据训练数据学习参数(w1,w2, ... , wn,b ...
- Spark MLlib回归算法------线性回归、逻辑回归、SVM和ALS
Spark MLlib回归算法------线性回归.逻辑回归.SVM和ALS 1.线性回归: (1)模型的建立: 回归正则化方法(Lasso,Ridge和ElasticNet)在高维和数据集变量之间多 ...
- 机器学习(三)—线性回归、逻辑回归、Softmax回归 的区别
1.什么是回归? 是一种监督学习方式,用于预测输入变量和输出变量之间的关系,等价于函数拟合,选择一条函数曲线使其更好的拟合已知数据且更好的预测未知数据. 2.线性回归 于一个一般的线性模型而言,其 ...
随机推荐
- tomcat容器是如何创建servlet类实例?用到了什么原理?
当容器启动时,会读取在webapps目录下所有的web应用中的web.xml文件,然后对 xml文件进行解析,并读取servlet注册信息.然后,将每个应用中注册的servlet类都进行加载,并通过 ...
- 前端下载excel文件功能的三种方法
1 从后端接收json数据,前端处理生成excel下载 JsonExportExcel的github地址:https://github.com/cuikangjie/JsonExportExcel 这 ...
- JS闭包与JS函数
先说说在网上看到的一个闭包案例: var add = (function () {var counter = 0;return function () {return counter += 1;}}) ...
- Mac 远程连接 Windows
推荐使用微软官方发布的 Microsoft Remote Desktop,免费.流畅. 详见:https://docs.microsoft.com/en-us/windows-server/remot ...
- 使用commit方式构建具有sshd服务的centos镜像
一般我们是通过SSH服务来管理服务器的,但是现在很多Docker镜像不带SSH服务,那我们该如何来管理这些容器呢?现在我们通常使用attach和nsenter工具.但是都无法解决远程管理容器的问题,当 ...
- bigdata-01-应用
1, 基本概念 在互联网技术发展到现今阶段,大量日常.工作等事务产生的数据都已经信息化,人类产生的数据量相比以前有了爆炸式的增长,以前的传统的数据处理技术已经无法胜任,需求催生技术,一套用来处理海量数 ...
- FFmpeg编解码处理1-转码全流程简介
本文为作者原创,转载请注明出处:https://www.cnblogs.com/leisure_chn/p/10584901.html FFmpeg编解码处理系列笔记: [0]. FFmpeg时间戳详 ...
- Form的enctype属性
Form的enctype属性 一般都使用html的Form表单通过HTTP POST方法发送Request body.下面是一个form: <form action="/process ...
- 将不确定变为确定~老赵写的CodeTimer是代码性能测试的利器
首先,非常感谢赵老大的CodeTimer,它让我们更好的了解到代码执行的性能,从而可以让我们从性能的角度来考虑问题,有些东西可能我们认为是这样的,但经理测试并非如何,这正应了我之前的那名话:“机器最能 ...
- [PHP]算法-归并排序的PHP实现
<?php //归并排序 function merge(&$A,$left,$mid,$right,$temp){ //7.左堆起始 $i=$left; //8.右堆起始 $j=$mid ...
