[JZOJ4913] 【GDOI2017模拟12.3】告别

题目

描述

题目大意

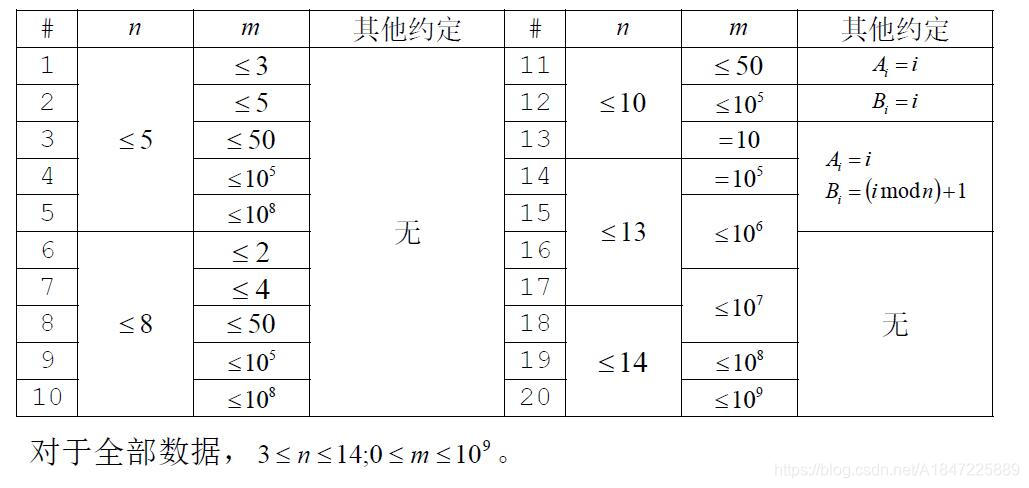
给你两个排列AAA和BBB，每次随即选三个数进行轮换操作，问mmm次操作内使AAA变成BBB的概率。

---

思考历程

首先随便搞一下，就变成了AAA中每个数回归自己原位。

一眼望去，感觉nnn很小……

最简单的想法是将每个情况都储存起来，然后搞出它们之间的转移情况。

然后发现这些状态是存不下的。

于是我就开始想有没有哪些状态是等价的。

然后我发现对于每个数字，可以简单地归为是否回归原位的两种情况。这样状态倒小了，可是又能怎么转移呢？mmm这么大，肯定打矩阵乘法。这么大的状态还是不能过啊！

于是我就放弃了希望：还能怎么压？

---

正解

题解的方法真是令人惊叹。

不过题解说得晦涩难懂，我还是用人话来解决一下。

我们可以把当前的数组看成一个边集，表示从某个点连向另一个点。

显然点数有nnn个，边数nnn个，并且每个点有且仅有一个出度（和入度）。

那么这个图就是由几个环组成的。

如果我们将同环中的三个数拿出来轮换，轮换过后它们依然能够在这个环中，环的大小不变。

我们可以感性地理解它为等价的。

那么我们换一下状态的表示方法。对于每个状态，我们记录每个环的大小，用个桶来存它。

环的内部结构具体是什么可以不用去理睬它，我们只知道这些都是一样的，这就足够了（感性大法好）。

显然，每个数回归到自己原位就相当于是nnn个环，这种情况只会有一种，我们最终要算出来的是这个的答案，所以不会被其它杂七杂八的东西给影响（假设这个状态的编号为111）

让我们算一算这样压缩状态的状态数，然后就可以发现这是nnn的划分数，当n=14n=14n=14时只有135135135。

这么小的数据，当然可以矩阵乘法了。

于是我们就开始设fi,jf_{i,j}fi,j​为状态iii转移到状态jjj的概率。

有个问题是如何转移。

一开始我想了很久，但最后才发现我想复杂了。实际上有个最简单也最粗暴的方法：造出一个排列！

随便造出一个满足这个状态的排列，然后O(n3)O(n^3)O(n3)地转移，将转移过后的排列变成状态。这样就可以记录了。

当然，要用个mapmapmap或打哈希表来记录每种状态的编号。

由于nnn很小，这样跑还特别快。

最后是要注意的地方，题目说在mmm次操作内复原，所以到了111状态后，就不需要再转移出来了。

也就是f1,1=1f_{1,1}=1f1,1​=1且对于i>1i> 1i>1，使得f1,i=0f_{1,i}=0f1,i​=0

时间复杂度就不用分析了吧……

---

代码

using namespace std;
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <map>
#define mo 998244353
map<long long,int> bz;
int n,invn3,m;
int a[15],b[15],c[15];
long long my_hash(int s[]){
	long long res=0;
	for (int i=n;i>=1;--i)
		res=res*(n+1)+s[i];
	return res;
}
int s[15];
void fors(int k,int sum,int i,void work()){//枚举状态……套了个函数
	if (sum==0){
		work();
		return;
	}
	for (;i<=sum;++i){
		s[i]++;
		fors(k+1,sum-i,i,work);
		s[i]--;
	}
}
int cnt;
void init(){
	bz[my_hash(s)]=++cnt;
}
int *tran(int *a){
	static bool vis[15];
	static int s[15];
	memset(vis,0,sizeof vis);
	memset(s,0,sizeof s);
	for (int i=0;i<n;++i){
		if (vis[i])
			continue;
		int c=0;
		for (int j=i;!vis[j];j=a[j],c++)
			vis[j]=1;
		s[c]++;
	}
	return s;
}
struct Matrix{
	int mat[151][151];
	inline void operator*=(Matrix &b){
		static Matrix res;
		for (int i=1;i<=cnt;++i)
			for (int j=1;j<=cnt;++j){
				long long sum=0;
				for (int k=1;k<=cnt;++k)
					sum+=1ll*mat[i][k]*b.mat[k][j]%mo;
				res.mat[i][j]=sum%mo;
			}
		memcpy(mat,res.mat,sizeof res);
	}
	inline void get_pow(int n){
		static Matrix res;
		memset(res.mat,0,sizeof res);
		for (int i=1;i<=cnt;++i)
			res.mat[i][i]=1;
		for (;n;n>>=1,*this*=*this)
			if (n&1)
				res*=*this;
		memcpy(this,res.mat,sizeof res);
	}
} f;
void calc(){
	static int tmp[15],tmp2[15];
	int numt=bz[my_hash(s)];
	if (numt==1){
		f.mat[1][1]=1;
		return;
	}
	for (int i=1,j=0;i<=n;++i)//造一个序列
		for (int k=0;k<s[i];++k){
			int jj=j;
			for (;j<jj+i;++j)
				tmp[j]=j-1;
			tmp[jj]=j-1;
		}
	memcpy(tmp2,tmp,sizeof tmp);
	for (int i=0;i<n;++i)
		for (int j=0;j<n;++j)
			if (i!=j)
				for (int k=0;k<n;++k)
					if (i!=k && j!=k){
						tmp2[i]=tmp[k],tmp2[j]=tmp[i],tmp2[k]=tmp[j];
						int numt2=bz[my_hash(tran(tmp2))];
						(f.mat[numt][numt2]+=invn3)%=mo;
						tmp2[i]=tmp[i],tmp2[j]=tmp[j],tmp2[k]=tmp[k];
					}
}
int main(){
	freopen("goodbye.in","r",stdin);
	freopen("goodbye.out","w",stdout);
	scanf("%d%d",&n,&m);
	invn3=1;
	for (int i=mo-2,tmp=1ll*n*(n-1)%mo*(n-2)%mo;i;i>>=1,tmp=1ll*tmp*tmp%mo)
		if (i&1)
			invn3=1ll*invn3*tmp%mo; //invn3=(n*(n-1)*(n-2))^(-1)
	for (int i=0;i<n;++i){
		scanf("%d",&a[i]);
		a[i]--;
	}
	for (int i=0;i<n;++i){
		scanf("%d",&b[i]);
		b[i]--;
		c[b[i]]=a[i];
	}

	fors(0,n,1,init);
	fors(0,n,1,calc);
	f.get_pow(m);
	int numa=bz[my_hash(tran(c))];
	printf("%d\n",f.mat[numa][1]);
	return 0;
}

用的语法可能有点骚……不过应该能看懂吧？

---

总结

这道题的压缩手段，不可不谓是极致了。