洛谷 P1044 栈

题目背景

栈是计算机中经典的数据结构，简单的说，栈就是限制在一端进行插入删除操作的线性表。

栈有两种最重要的操作，即pop（从栈顶弹出一个元素）和push（将一个元素进栈）。

栈的重要性不言自明，任何一门数据结构的课程都会介绍栈。宁宁同学在复习栈的基本概念时，想到了一个书上没有讲过的问题，而他自己无法给出答案，所以需要你的帮忙。

题目描述

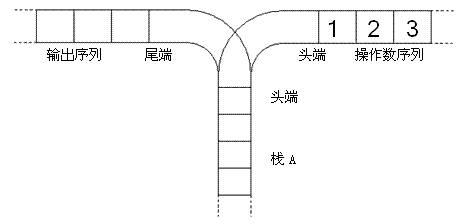
宁宁考虑的是这样一个问题：一个操作数序列，从1，2，一直到n（图示为1到3的情况），栈A的深度大于n。

现在可以进行两种操作，

1.将一个数，从操作数序列的头端移到栈的头端（对应数据结构栈的push操作）

1. 将一个数，从栈的头端移到输出序列的尾端（对应数据结构栈的pop操作）

使用这两种操作，由一个操作数序列就可以得到一系列的输出序列，下图所示为由1 2 3生成序列2 3 1的过程。

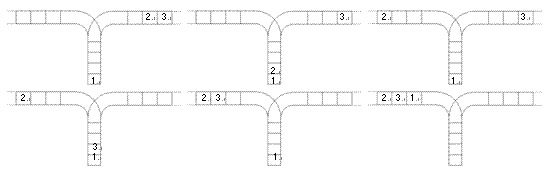
（原始状态如上图所示）

你的程序将对给定的n，计算并输出由操作数序列1，2，…，n经过操作可能得到的输出序列的总数。

输入输出格式

输入格式：

输入文件只含一个整数n（1≤n≤18）

输出格式：

输出文件只有一行，即可能输出序列的总数目

输入输出样例

输入样例#1：

3

输出样例#1：

5

假设j最后一个出栈，那么前j-1个数在之前都以入栈出栈，后n-j个数在j之后入栈，且已经出栈
前后相对独立，所以 f[n]=Σ f[j-1]*f[n-j]

#include<cstdio>
using namespace std;
int f[];
int main()
{
    int n;
    scanf("%d",&n);
    f[]=f[]=;
    for(int i=;i<=n;i++)
     for(int j=;j<=i;j++)
      f[i]+=f[j-]*f[i-j];
    printf("%d",f[n]);
}