用列主元消去法分别解方程组Ax=b，用MATLAB程序实现（最有效版）

数值分析里面经常会涉及到用MATLAB程序实现用列主元消去法分别解方程组Ax=b

具体的方法和代码以如下方程（3x3矩阵）为例进行说明：

用列主元消去法分别解方程组Ax=b，用MATLAB程序实现：

（1）

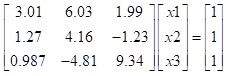
1、 实现该方程的解的MATLAB代码可以分为两种，一种是入门级别的，只是简单地计算出这道题即可，第二种是一种通用的代码，可以实现很多3x3矩阵的方程解，写好以后只需要改不同矩阵里的元素即可算出相应的解，需要建立在对MATLAB比较熟悉的基础上，具体如下：

第一种代码实现—入门级：

A=[3.01,6.03,1.99,;1.27,4.16,-1.23,;0.987,-4.81,9.34]

A1=[3.01,6.03,1.99,1;1.27,4.16,-1.23,1;0.987,-4.81,9.34,1]

B1=A1(1,1:4)

C1=A1(2,1:4)

D1=A1(3,1:4)

E1=-1.27/3.01*B1+C1

F1=-0.987/3.01*B1+D1

p1=E1(1,2)

q1=F1(1,2)

if (abs(p1)>=abs(q1))

    a1=p1

    a2=q1

    FF1=E1

    EE1=F1

else

    a1=q1

    a2=p1

    FF1=F1

    EE1=E1

end

G1=-a2/a1*FF1+EE1

H1=[E11;FF1;G1]

J1=H1(1:3,1:3)

b1=H1(1:3,4)

x1=J1\b1

第二种代码实现如下—熟练通用级：

A=[3.01,6.03,1.99,;1.27,4.16,-1.23,;0.987,-4.81,9.34]

A1=[3.01,6.03,1.99,1;1.27,4.16,-1.23,1;0.987,-4.81,9.34,1]

B1=A1(1,1:4)

C1=A1(2,1:4)

D1=A1(3,1:4)

f1=A1(1,1)

f2=A1(2,1)

f3=A1(3,1)

if (abs(f1)>=abs(f2))

    if(abs(f1)>=abs(f3))

        f11=f1

        E11=B1

        f22=f2

        E12=C1

        f33=f3

        E13=D1

    else

        f11=f3

        E11=D1

        f22=f1

        E12=B1

        f33=f2

        E13=C1

    end

end

    if(abs(e2)>=abs(e3))

        f11=f2

        E11=C1

        f22=f1

        E12=B1

        f33=f3

        E13=D1

    else

        f11=f3

        E11=D1

        f22=f1

        E12=B1

        f33=f2

        E13=C1

    end   

E1=-f22/f11*E11+E12

F1=-f33/f11*E11+E13

p1=E1(1,2)

q1=F1(1,2)

if (abs(p1)>=abs(q1))

    a1=p1

    a2=q1

    FF1=E1

    EE1=F1

else

    a1=q1

    a2=p1

    FF1=F1

    EE1=E1

end

G1=-a2/a1*FF1+EE1

H1=[E11;FF1;G1]

J1=H1(1:3,1:3)

b1=H1(1:3,4)

x1=J1\b1

输出结果如下：

A =

3.0100    6.0300    1.9900

1.2700    4.1600   -1.2300

0.9870   -4.8100    9.3400

A1 =

3.0100    6.0300    1.9900    1.0000

1.2700    4.1600   -1.2300    1.0000

0.9870   -4.8100    9.3400    1.0000

B1 =

3.0100    6.0300    1.9900    1.0000

C1 =

1.2700    4.1600   -1.2300    1.0000

D1 =

0.9870   -4.8100    9.3400    1.0000

f1 =

3.0100

f2 =

1.2700

f3 =

0.9870

f11 =

3.0100

E11 =

3.0100    6.0300    1.9900    1.0000

f22 =

1.2700

E12 =

1.2700    4.1600   -1.2300    1.0000

e33 =

0.9870

E13 =

0.9870   -4.8100    9.3400    1.0000

e11 =

1.2700

E11 =

1.2700    4.1600   -1.2300    1.0000

e22 =

3.0100

E12 =

3.0100    6.0300    1.9900    1.0000

e33 =

0.9870

E13 =

0.9870   -4.8100    9.3400    1.0000

E1 =

0   -3.8295    4.9052   -1.3701

F1 =

0   -8.0430   10.2959    0.2228

p1 =

-3.8295

q1 =

-8.0430

a1 =

-8.0430

a2 =

-3.8295

FF1 =

0   -8.0430   10.2959    0.2228

EE1 =

0   -3.8295    4.9052   -1.3701

G1 =

0         0    0.0030   -1.4762

H1 =

1.2700    4.1600   -1.2300    1.0000

0   -8.0430   10.2959    0.2228

0         0    0.0030   -1.4762

J1 =

1.2700    4.1600   -1.2300

0   -8.0430   10.2959

0         0    0.0030

b1 =

1.0000

0.2228

-1.4762

x1 =

   1592.6

   -631.9

   -493.6

可以看出：两种代码的区别在于列主元方法中每一步对每一列最大主元的判断上面，第一种直接看出来，所以就用具体的数字代替了，而第二种对变量进行了一般性的定义和赋值，通过if语句进行大小判断，这样的方法会比较通用，建立在对于MATLAB熟练的基础上。