CF311E Biologist

嘟嘟嘟

很显然是一道最小割模型。

做完几道题后。图的大概就能想出来了：

1.对于每一个动物，如果是0，就和s连一条边，否则向t连一条边。

2.对于每一个任务，题中要求最大利润，可以转化成最小损失。

　　(1)如果都要变成1，就向汇点连一条w +g(如果有的话)的边；否则从源点连一条w +g的边。接下来

　　(2)对于任务中涉及的每一个点，刚开始我想如果任务要变成1，而他本身还是1就不连边，否则连一条INF的边，然后我就发现任务之间是互相影响的，而这种方式体现不出来，然后我就想不出来了……

　　   题解是这么说的：如果这个任务是0，就向所有涉及到的点连边，否则这些点向他连边，然后我就画了一个图，发现好像还真是这么回事：

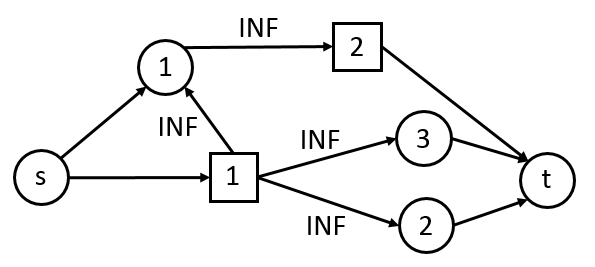
如果我们要达成任务1的话，就要割掉(2->t), (3->t)两条边，但是图还是联通的，因此还得割掉([2]->t)的边，也就同时说明了任务2不可达成。

 #include<cstdio>
 #include<iostream>
 #include<cmath>
 #include<algorithm>
 #include<cstring>
 #include<cstdlib>
 #include<cctype>
 #include<vector>
 #include<stack>
 #include<queue>
 using namespace std;
 #define enter puts("")
 #define space putchar(' ')
 #define Mem(a, x) memset(a, x, sizeof(a))
 #define rg register
 typedef long long ll;
 typedef double db;
 const int INF = 0x3f3f3f3f;
 const db eps = 1e-;
 const int maxn = 1.2e4 + ;
 inline ll read()
 {
     ll ans = ;
     char ch = getchar(), last = ' ';
     while(!isdigit(ch)) {last = ch; ch = getchar();}
     while(isdigit(ch)) {ans = ans *  + ch - ''; ch = getchar();}
     if(last == '-') ans = -ans;
     return ans;
 }
 inline void write(ll x)
 {
     if(x < ) x = -x, putchar('-');
     if(x >= ) write(x / );
     putchar(x %  + '');
 }

 int n, m, t;
 int g, val[maxn], sum = ;
 bool a[maxn];

 struct Edge
 {
     int from, to, cap, flow;
 };
 vector<Edge> edges;
 vector<int> G[maxn];
 void addEdge(int from, int to, int w)
 {
     edges.push_back((Edge){from, to, w, });
     edges.push_back((Edge){to, from, , });
     int sz = edges.size();
     G[from].push_back(sz - );
     G[to].push_back(sz - );
 }

 int dis[maxn];
 bool bfs()
 {
     Mem(dis, ); dis[] = ;
     queue<int> q; q.push();
     while(!q.empty())
     {
         int now = q.front(); q.pop();
         for(int i = ; i < (int)G[now].size(); ++i)
         {
             Edge& e = edges[G[now][i]];
             if(!dis[e.to] && e.cap > e.flow)
             {
                 dis[e.to] = dis[now] + ;
                 q.push(e.to);
             }
         }
     }
     return dis[t];
 }
 int cur[maxn];
 int dfs(int now, int res)
 {
     if(now == t || res == ) return res;
     int flow = , f;
     for(int& i = cur[now]; i < (int)G[now].size(); ++i)
     {
         Edge& e = edges[G[now][i]];
         if(dis[e.to] == dis[now] +  && (f = dfs(e.to, min(res, e.cap - e.flow))) > )
         {
             e.flow += f;
             edges[G[now][i] ^ ].flow -= f;
             flow += f; res -= f;
             if(res == ) break;
         }
     }
     return flow;
 }

 int minCut()
 {
     int flow = ;
     while(bfs())
     {
         Mem(cur, );
         flow += dfs(, INF);
     }
     return flow;
 }

 int main()
 {
     n = read(), m = read(), g = read();
     t = n + m + ;
     for(int i = ; i <= n; ++i) a[i] = (bool)read();
     for(int i = ; i <= n; ++i)
     {
         int x = read();
         if(a[i]) addEdge(i, t, x);
         else addEdge(, i, x);
     }
     for(int i = ; i <= m; ++i)
     {
         int op = read(), w = read(), k = read();
         sum += w;
         for(int j = ; j <= k; ++j)
         {
             int id = read();
             if(op) addEdge(id, i + n, INF);
             else addEdge(i + n, id, INF);
         }
         int flg = read();
         if(op) addEdge(i + n, t, w + flg * g);
         else addEdge(, i + n, w + flg * g);
     }
     write(sum - minCut()); enter;
     return ;
 }