【hdu1705】Count the grid（皮克定理）

链接：http://acm.hdu.edu.cn/showproblem.php?pid=1705

【题意】

给出平面上三个点坐标，求围成的三角形内部的点数

做这道题需要先了解下皮克定理。

百度百科：皮克定理是指一个计算点阵中顶点在格点上的多边形面积公式，该公式可以表示为2S=2a+b-2，其中a表示多边形内部的点数，b表示多边形边界上的点数，s表示多边形的面积。

多边形边界上的整数点怎么求呢？

当然是gcd啦~~  gcd(x1-x2, y1-y2)就是这条边上整数点的个数。但是仅仅一条边是不准确的（有一个端点没有算上），需要把所有边的gcd加上才是皮克定理中的「b」。

面积怎么求呢？

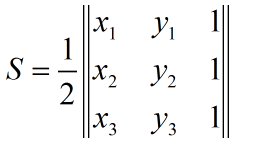
然后就可以开心地求出a啦~

 #include <bits/stdc++.h>
 using namespace std;
 typedef long long LL;
 struct q
 {
     LL x, y;
 } co[];
 LL area()
 {
     return abs(co[].x*(co[].y-co[].y)-co[].y*(co[].x-co[].x)+co[].x*co[].y-co[].x*co[].y);//算出来可能为负数，所以abs
 }
 LL gcd(LL a, LL b)
 {
     if(a < b) swap(a, b); //a如果小于b的话要交换位置
     if(b == ) return a;
     return gcd(b,a%b);
 }
 int main()
 {
     while()
     {
         scanf("%lld%lld%lld%lld%lld%lld", &co[].x, &co[].y, &co[].x, &co[].y, &co[].x, &co[].y);
         if(co[].x==&&co[].y==&&co[].x==&&co[].y==&&co[].x==&&co[].y==) break;
         double s = area() / 2.0;
         LL ab = gcd(abs(co[].x - co[].x), abs(co[].y - co[].y));
         LL bc = gcd(abs(co[].x - co[].x), abs(co[].y - co[].y));
         LL ac = gcd(abs(co[].x - co[].x), abs(co[].y - co[].y));
         LL in = s - (ab + bc + ac) / 2.0 + ;
         printf("%lld\n", in);
     }
     return ;
 }