BZOJ2246 [SDOI2011]迷宫探险 【记忆化搜索dp + 概率】

题目

输入格式

输出格式

仅包含一个数字，表示在执行最优策略时，人物活着走出迷宫的概率。四舍五入保留3位小数。

输入样例

4 3 3 2

.$.

A#B

A#C

@@@

143 37 335 85 95 25 223 57

输出样例

0.858

提示

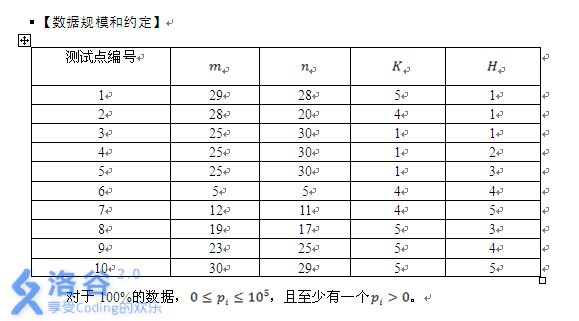
题解

毒瘤dp题

我们设\(f[x][y][s][h]\)表示从点\((x,y)\)出发，所有陷阱状态为\(s\)，生命值为\(h\)，存活的期望概率

我们枚举邻点，选择存活概率最大的作为当前\(f\)的值

除了墙，有以下情况：

①如果是空地或者终点，直接转移\(f[nx][ny][s][h]\)

②如果是陷阱：

1、如果陷阱已知

无害则同空地的转移

有害则转移的同时\(h - 1\)

2、如果陷阱位置

那么就是\(g[s][t] * f[nx][ny][s'][h - 1] + (1 - g[s][t]) * f[nx][ny][s''][h]\)

其中\(g[s][t]\)表示在已知状态为s的情况下，陷阱\(t\)有害的概率，可以预处理出来

\(s'\)和\(s''\)就是加入新状态的s

至于g数组的预处理，对于每种s，枚举未知位置的子集，将各种情况有害的加到对应陷阱去，然后除以总值

为什么换一个搜索顺序才能A？？？

#include<iostream>
#include<cstdio>
#include<cctype>
#include<cstring>
#include<algorithm>
#define REP(i,n) for (int i = 1; i <= (n); i++)
using namespace std;
inline int read(){
	int out = 0,flag = 1; char c = getchar();
	while (c < 48 || c > 57){if (c == '-') flag = -1; c = getchar();}
	while (c >= 48 && c <= 57){out = (out << 3) + (out << 1) + c - 48; c = getchar();}
	return out * flag;
}
double f[32][32][250][6],g[250][6],p[100];
int vis[32][32][250][6],bin[10];
int n,m,K,H,Sx,Sy,X[4] = {1,0,-1,0},Y[4] = {0,-1,0,1};
int G[32][32];
void init(){
	n = read(); m = read(); K = read(); H = read();
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= m; j++){
			char c = getchar();
			while (!isprint(c)) c = getchar();
			if (c == '.') G[i][j] = 0;
			else if (c == '#') G[i][j] = -1;
			else if (c == '$') G[i][j] = 0,Sx = i,Sy = j;
			else if (c == '@') G[i][j] = -2;
			else G[i][j] = c - 'A' + 1;
		}
	//REP(i,n) {REP(j,m) printf("%d ",G[i][j]); puts("");}
	bin[0] = 1;
	for (int i = 1; i <= K; i++) bin[i] = bin[i - 1] * 3;
	//REP(i,K) printf("%d ",bin[i]); puts("");
	int maxv = (1 << K) - 1,maxp = bin[K] - 1;
	for (int s = 0; s <= maxv; s++) p[s] = read();
	for (int s = 0; s <= maxp; s++){
		int e = 0,t = 0; double sum = 0;
		for (int i = s,j = 1; j <= K; j++,i /= 3){
			if (i % 3 == 0) t |= (1 << j - 1);
			else if (i % 3 == 2) e |= (1 << j - 1);
		}
		for (int i = t; ; i = (i - 1) & t){
			int to = (e | i);
			sum += p[to];
			for (int j = 1; j <= K; j++)
				if (to & (1 << j - 1)) g[s][j] += p[to];
			if (!i) break;
		}
		for (int i = 1; i <= K; i++)
			g[s][i] /= sum;
	}
}
double F(int x,int y,int s,int h){
	if (vis[x][y][s][h]) return f[x][y][s][h];
	if (h == 0){
		vis[x][y][s][h] = 1;
		return f[x][y][s][h] = 0;
	}
	if (G[x][y] == -2){
		vis[x][y][s][h] = 1;
		return f[x][y][s][h] = 1;
	}
	vis[x][y][s][h] = 1;
	double& ff = f[x][y][s][h];
	ff = 0;
	int nx,ny;
	for (int k = 0; k < 4; k++){
		nx = x + X[k];
		ny = y + Y[k];
		if (nx < 1 || ny < 1 || nx > n || ny > m || G[nx][ny] == -1) continue;
		if (G[nx][ny] == 0 || G[nx][ny] == -2){
			ff = max(ff,F(nx,ny,s,h));
		}
		else {
			int t = G[nx][ny];
			if ((s / bin[t - 1]) % 3 == 1) ff = max(ff,F(nx,ny,s,h));
			else if ((s / bin[t - 1]) % 3 == 2) ff = max(ff,F(nx,ny,s,h - 1));
			else {
				ff = max(ff,g[s][t] * F(nx,ny,s + 2 * bin[t - 1],h - 1) + (1 - g[s][t]) * F(nx,ny,s + bin[t - 1],h));
			}
		}
	}
	return ff;
}
int main(){
	init();
	if (n == 0) return 0;
	else printf("%.3lf\n",F(Sx,Sy,0,H));
	return 0;
}