TVM图优化（以Op Fusion为例）

首先给出一个TVM 相关的介绍，这个是Tianqi Chen演讲在OSDI18上用的PPThttps://files.cnblogs.com/files/jourluohua/Tianqi-Chen-TVM-Stack-Overview.rar

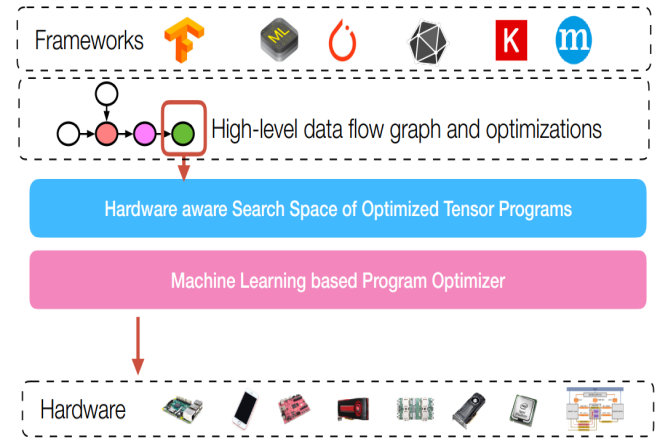
对于图优化来说，位于整个软件编译栈比较高的层次：

首先给出计算图的定义

Computational graphs: a common way to represent programs in deep learning frameworks

对于图优化来说，有很多种图优化手段：Operator Fusion
Constant Parameter Path Pre-Computation
Static Memory Reuse Analysis
Data Layout Transformation
AlterOpLayout
SimplifyInference

这里仅以Operator Fusion做例子介绍

Operator fusion : combine multiple operators together into a single kernel without saving the intermediate results back into global memory

也就说是说算子融合省掉了中间数据的store过程

在TVM中，有三种融合规则：

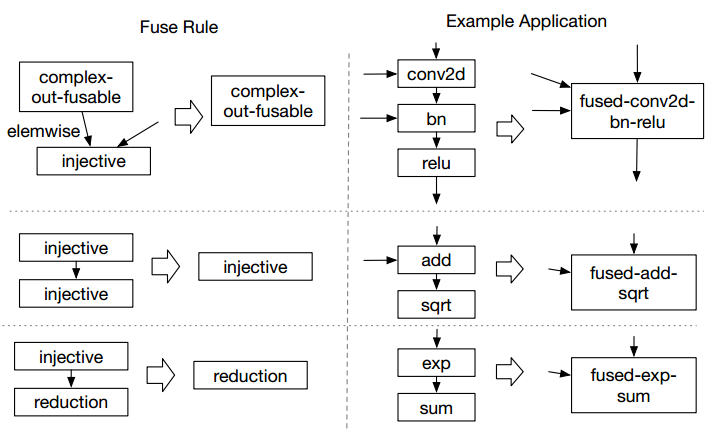
其中，算子属于哪一类是算子本身的特性（这个地方不是特别懂，这个属性有非常多的值），但是能融合的规则只有这三种。

但是这种store是如何减少的，在IR上有明确的体现。

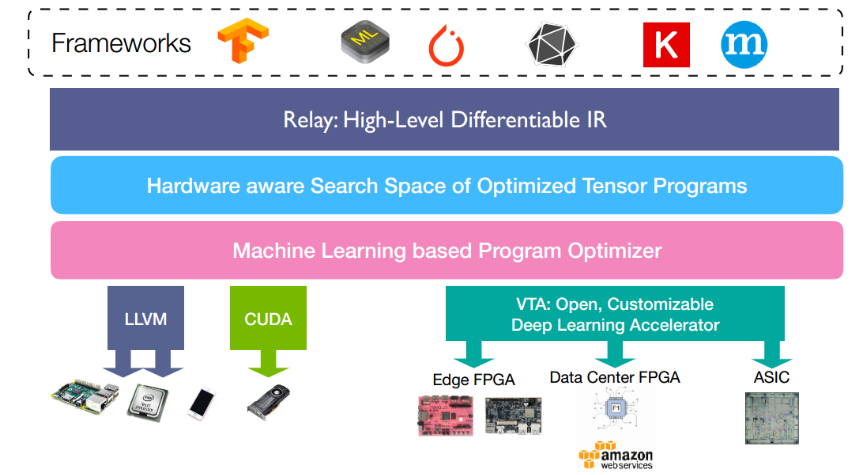
下边的例子，我会使用tvm.relay来进行介绍，relay是TVM中实现的一种高级IR，可以简单理解为另一种计算图表示。其在TVM所处的位置如下图所示

比如，我们假设我们要完成一个y = exp(x+1.0)的计算图

给出测试代码(来自于源码中的test_pass_fuse_ops.py，有改动)：

import tvm
from tvm import relay

def test_fuse_simple():
    """Simple testcase."""
    def before():
        x = relay.var("x", shape=(10, 20))
        y = relay.add(x, relay.const(1, "float32"))
        z = relay.exp(y)
        return relay.Function([x], z)

    def expected():
        x = relay.var("p", shape=(10, 20))
        y = relay.add(x, relay.const(1, "float32"))
        z = relay.exp(y)
        f1 = relay.Function([x], z)
        x = relay.var("x", shape=(10, 20))
        y = relay.Call(f1, [x])
        return relay.Function([x], y)

    z = before()
    z = relay.ir_pass.infer_type(z)
    # print(z.astext())
    zz = relay.ir_pass.fuse_ops(z, opt_level=2)
    print(zz.astext())
    zz = relay.ir_pass.infer_type(zz)
    zz = relay.ir_pass.fuse_ops(zz)
    zz = relay.ir_pass.infer_type(zz)
    after = relay.ir_pass.infer_type(expected())
    # print(after.astext())
    assert relay.ir_pass.alpha_equal(zz, after)

在融合前，其IR(方便用户看的一种形式，不是真正的IR)

fn (%x: Tensor[(10, 20), float32])
    -> Tensor[(10, 20), float32] {
  %0 = fn(%p0: Tensor[(10, 20), float32],
          %p1: float32)
          -> Tensor[(10, 20), float32] {
    %1 = add(%p0, %p1)
    %1
  }
  %2 = %0(%x, 1f)
  %3 = fn(%p01: Tensor[(10, 20), float32])
          -> Tensor[(10, 20), float32] {
    %4 = exp(%p01)
    %4
  }
  %5 = %3(%2)
  %5
}

融合后：

fn (%x: Tensor[(10, 20), float32])
    -> Tensor[(10, 20), float32] {
  %0 = fn(%p0: Tensor[(10, 20), float32])
          -> Tensor[(10, 20), float32] {
    %1 = add(%p0, 1f)
    %2 = exp(%1)
    %2
  }
  %3 = %0(%x)
  %3
}

可以很明显的发现，省掉了一次数据store过程