梯度下降算法 Gradient Descent

梯度下降算法 Gradient Descent

梯度下降算法是一种被广泛使用的优化算法。在读论文的时候碰到了一种参数优化问题：

在函数\(F\)中有若干参数是不确定的，已知\(n\)组训练数据，期望找到一组参数使得残差平方和最小。通俗一点地讲就是，选择最合适的参数，使得函数的预测值与真实值最相符。

\[\{ n^*,m^*,p^* ...\} = arg \ \mathop{min} _{\{n,m,p,.. \} } \sum_{i=1}^n (\hat{f}_i - f_i)^2
\]

其中，\(\hat{f}\)为真实值，\(f\)为测量值。在函数\(F\)中，存在n,m,p等参数，也存在自变量。训练数据给出了若干组自变量与真实值，算法需要找到合适的参数使得函数与训练数据相符。

这时就要用到今天的算法：梯度下降算法！

梯度下降算法的分类：

• 梯度下降算法 Batch Gradient Descent
• 随机梯度下降算法 Stochastic Gradient Descent
• 小批量梯度下降算法 Mini-batch Gradient Descent

梯度下降算法

在梯度下降算法中，我们根据梯度方向，迭代地调整参数。我们把所有参数（例如n,m,p之类的）打包进一个变量组\(\theta=\{n,m,p,..\}\)，然后对这个变量组迭代更新；定义函数\(L=\sum_{i=1}^n (\hat{f}_i - f_i)^2\)为误差函数。

\[\theta^{t+1}=\theta^t- r\times \nabla_\theta L
\]

其中，\(r\)为学习率。r的大小决定了参数移动的“步幅”，若r值过小，往往需要更长的时间才能算出结果；而值过大又可能导致无法得到最优值。

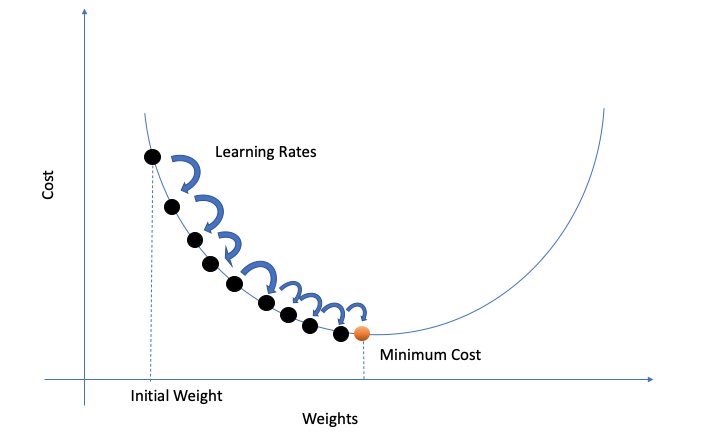
梯度的方向是函数增大最快的方向，那么梯度的反方向就是减小最快的方向。因此我们沿着梯度更小的方向进行参数更新可以有效地找到全局最优解。

def SGD(f, theta0, alpha, num_iters):
	"""
	Arguments:
	f -- the function to optimize, it takes a single argument
			and yield two outputs, a cost and the gradient
			with respect to the arguments
	theta0 -- the initial point to start SGD from
	num_iters -- total iterations to run SGD for
	Return:
	theta -- the parameter value after SGD finishes
	"""
	theta = theta0
	for iter in range(num_iters):
	# For python 2.x - use xrange
		grad = f(theta)[1]

		# there is NO dot product ! return theta
		theta = theta - r*(alpha * grad)

随机梯度下降算法

梯度下降算法看似已经解决了问题，但是还面临着“数据运算量过大”的问题。假设一下，我们现在有10000组训练数据，有10个参量，那么仅迭代一次就产生了10000*10=100000次运算。如果想让它迭代1000次的话，就需要10^8的运算量。显然易见，这个算法没法处理大规模的数据。

那么如何改进呢？在一次迭代中，将训练数据的量由“全体”改为“随机的一个”。这便是随机梯度下降算法（SGD）

优点：

打个比方，我们开发了一个新的软件，需要向100个用户收集体验数据并进行产品升级。在梯度下降方法中，我们会先向这100个用户挨个询问，然后进行一次优化；再挨个询问，再进行一次调整...在随机梯度下降方法中，我们会在询问完第一个用户之后就进行一次优化，然后拿着优化后的用户询问第二个客户，然后再优化；这样我们在完成一轮调查之后，就已经调整了100次！可以大大提高运行效率！

缺点：

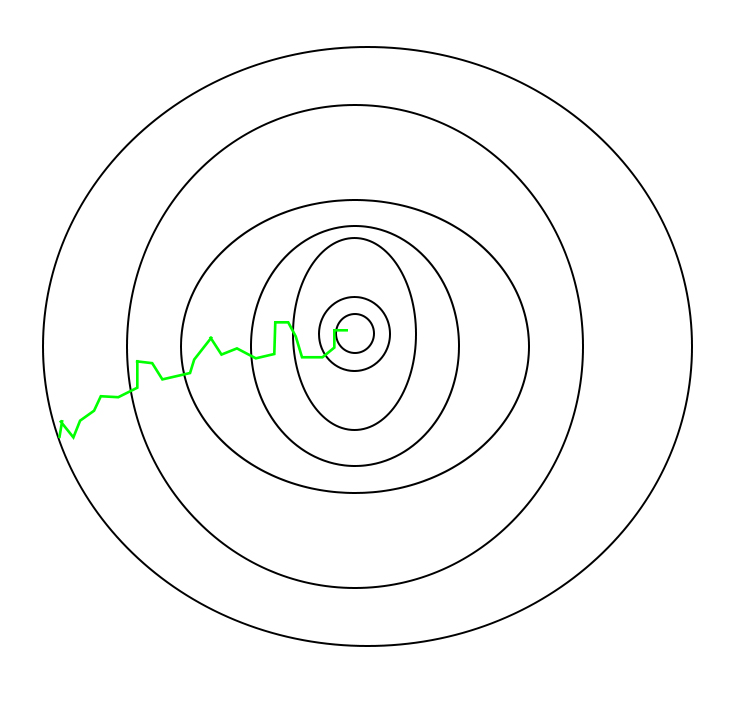
但是SGD在接近最优点之后很难稳定下来，而是在最优点附近徘徊，而难以到达最优。这一问题可以通到在后期适度降低学习率来解决。

并且由于随机性较大，所以下降的过程中较为曲折：

小批量梯度下降算法

小批量梯度下降算法则是吸收了前两者的优点。该算法存在一个变量Batch_size，指一次迭代中随机的选择多少的训练数据。如果Batch_size=n,就是梯度下降算法；如果Batch_size=1,就是随机梯度下降算法。

这样的小批量不仅可以减少计算的成本，还可以提高算法的稳定性。