leetcode210.拓扑排序

拓扑排序能否成功，其实就是看有没有环

• 有环：说明环内结点互为前置，永远也不可能完成
• 无环：是线性的，可以完成

DFS方法

思路：

逆向思维，遍历到边界点（无邻接点相当于叶子），再不断回溯将结点加入到结果中，得到的是拓扑排序的逆序，进行反转即可得到拓扑序列。

遍历过程中判断是否有环。

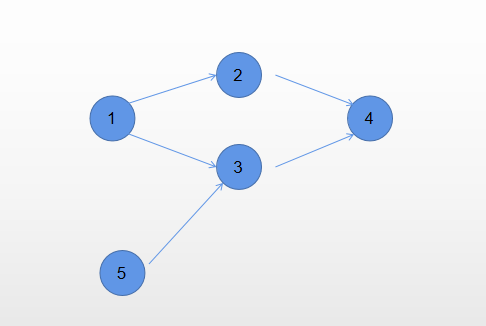
注意：要使用vist[]标记三种状态。假如只标记两种状态，则下面这种情况会判定为false，但其实是true

代码

class Solution {
    // 找到出度为0的点，
    vector<int> res;
    vector<int> g[2005];
    int vist[2005];     // 1:正在遍历中 0：未遍历   2：已经完成了遍历
    bool isLegal = true;
public:
    void dfs(int x){
        vist[x] = 1;
        for(int i = 0;i < g[x].size();i++){
            int nex = g[x][i];
            if(vist[nex] == 0){
                if(!isLegal) return ;
                dfs(nex);
            }else if(vist[nex] == 1){
                isLegal = false;
                return;
            }
        }
        vist[x] = 2;
        res.push_back(x);
    }

    vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
        int n = prerequisites.size();
        for(int i = 0;i < n;i++){
            int a = prerequisites[i][0], b = prerequisites[i][1];
            g[b].push_back(a);
        }
       for(int i = 0;i < numCourses;i++){
           if(!vist[i]) dfs(i);
       }

       if(!isLegal)    return {};
       reverse(res.begin(),res.end());
        return res;
    }
};

BFS方法

思路

正向，从入度为0的点开始正向遍历，使用每将一个点加入结果（删去），该点的邻接点的入度-1。若邻接点的入度减为0，则可以加入队列。最后结果集的数量应当等于课程的数量。

代码

/*
拓扑排序（BFS）
*/
#include <bits/stdc++.h>
using namespace std;

class Solution {
    // 构建图，并初始化每个结点的入度
    // 利用队列进行拓扑排序，不断的删除点，更新入度
    vector<int> res;
    int inDegree[2005];
    vector<int> g[2005];
public:
    vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
        int n = prerequisites.size();
        for(int i = 0;i < n;i++){
            int a = prerequisites[i][0], b = prerequisites[i][1];
            g[b].push_back(a);
            inDegree[a]++;
        }
        queue<int> q;
        // 寻找源点
        for(int i = 0;i < numCourses;i++){
            if(inDegree[i] == 0){
                q.push(i);
            }
        }
        while(!q.empty()){
            int now = q.front();
            q.pop();
            res.push_back(now);
            for(int i = 0;i < g[now].size();i++){
                inDegree[g[now][i]]--;
                if(inDegree[g[now][i]] == 0){
                    q.push(g[now][i]);
                }
            }
        }
        if(res.size() != numCourses)    return {};
        return res;
    }
};