FFT/NTT 学习笔记

0. 前置芝士

基础群论
复数

\(\mathbb C = \mathbb R[x^2+1]\)

则有 \(i^2+1=(-i)^2+1=0\)，\(i \in \mathbb C - \mathbb R\)

\(i^0=1;i^1=i;i^2=-1;i^3=-i;i^x=i^{x \bmod 4}(x \in \mathbb Z)\)

定理 0.1（欧拉公式）

\(e^{ik} = \cos k + i \sin k\)

证明：

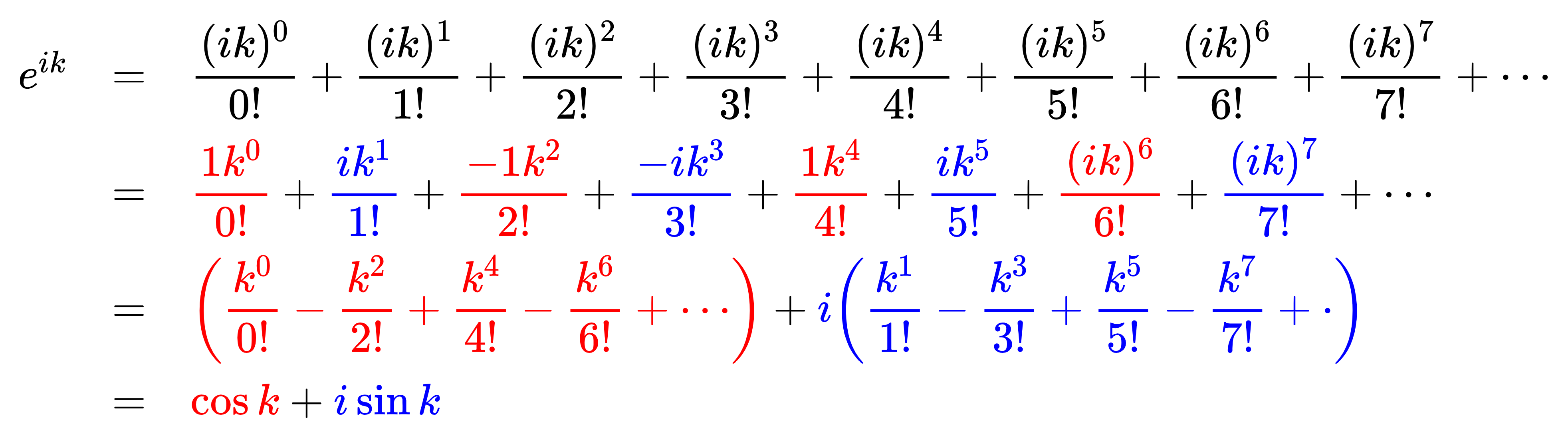
（因为这里辛辛苦苦打出来的 \(\sf \LaTeX\) 炸了，所以放了个图，不是贺的）

定义 0.2（单位根）

\(\omega_k := e^{\frac{2\pi i}k}\)
一些仅在本文生效的定义：

给定一个多项式 \(f(x)\) 和 \(i \le \deg f,f_i := \left\lfloor\dfrac f{x^i} \right\rfloor \bmod x\)。

本文中 \(f\) 和 \(f'\) 是两个函数，本文使用 \(\dfrac{{\rm d}f}{{\rm d}x}\) 表示导数。

1.引入

目标：求

\[h(x) = f(x) \times g(x) = \sum^{\deg f + \deg g}_{i=0}(x^i \times \sum_{a+b=i} f_a \times g_a)
\]

。

考虑取任意 \(\deg f + \deg g + 1\) 个复数 \(x_0,x_1,\dots,x_{\deg f + \deg g + 1}\)，则有 \(h(x_i) = f(x_i)g(x_i)\)，可以通过拉格朗日插值插回来（一般多项式题有 \(\deg f = \deg g\)，且会 \(\bmod x^{\deg f+1}\)，所以可以直接 \(x_0,x_1,\dots,x_{\deg f}\)，之后的讲解以这种方法为主）

取 \(x_i = -\omega_{\deg f+1}^i\)，则得到的 \(f(x_i) = \mathscr F f_i\)（此处 \(\mathscr F f\) 为长度为 \(\deg f+1\) 的序列而非多项式，且 \(\mathscr F f\) 的下标从 \(0\) 到 \(\deg f\)）

插值部分不需要拉格朗日，有一个神奇的柿子：\(\mathscr{F}^{-1} f = \frac{1}{\deg f+1} \sum_{k=0}^{\deg f} { f}_k {\omega}^{k}_{\deg f}\)

构造方法见 IFFT，但是建议把 \(\mathscr {F F}^{-1} f\) 展开看看正确性，这里就不推了

这两种东西被叫做 DFT 和 IDFT，根据定义式计算复杂度为 \(\mathcal O(n^2)\)

2.FFT

常数优化

定理 2.1 一个多项式 \(f(x)\) 一定能分成两部分 \(f(x)=O(x)+E(x)\)，使得 \(\forall x E(x)=E(-x) \wedge \forall x O(x) = -O(-x)\)

构造性证明：\(E(x) = f_0x^0+f_2x^2+f_4x^4+\cdots,O(x)=f_1x^1+f_3x^3+f_5x^5+\cdots\)。

P.S. 通过麦克劳林展开式，可以得到 \(f(x)\) 不一定是多项式。

定理 2.2 \(\omega_n^x=-\omega_n^{x+\frac n2}\)

证明：\(e^{\frac{2\pi i}n \times (x+\frac n2)}=e^{\frac{2\pi i}n \times x+ \frac{2\pi i}n \times \frac n2}=e^{\frac{2\pi}n \times x} \times e^{\pi i} = -e^{\frac{2\pi}n \times x} = -\omega^x_n\)。

所以我们计算 DFT 和 IDFT 的时候可以考虑少搞一半。

（因为这个定理在 FFT 的过程中要反复进行，所以这里建议把 \(f\) 补全到 \(2^n\) 项）。
分治（递归）

考虑分治地去完成 DFT。取代那一半的暴力运算，考虑变换出那一段：wait，一半的单位根和整个函数怎么变换？

定理 2.3 \((\omega_n^x)^2 = \omega_{\frac n2}^x\)

证明：\((\omega_n^x)^2 = (\omega_n^{2x}) = e^{\frac{2\pi i}n \times 2x} = e^{\frac{2\pi i}{n/2} \times x} = \omega_{\frac n2}^x\)

如果，我们跳出那思维呢？

设 \(E_f(x) = f_0x^0+f_2x^2+f_4x^4+\cdots,O_f(x)=f_1x^1+f_3x^3+f_5x^5+\cdots\)

令 \(E'_f(x) = E_f(\sqrt{x}); O'_f(x)=\dfrac {O_f(\sqrt{x})}{\sqrt{x}}\)

，则 \(2\deg E'_f-1 = 2\deg O'_f-1 = \deg f\)

有 \(f(x) = E'_f(x^2) + \omega_{2^n} O'_f(x^2)\)

当 \(x\) 是 \(2^n\) 次单位根的时候，\(x^2\) 一定是 \(2^{n-1}\) 次单位根，而正好 \(\deg E'_f = \deg O'_f = 2^{n-1}-1\)，所以进行递归，把 \(E'_f\) 和 \(O'_f\) 进行 FFT，就可以完成了。

边界条件：\(n=0\)，此时多项式变为一个常数，直接返回这个常数就可以了。
分治（非递归）

这里因为正好 \(\deg f = 2^n-1\)（有 \(2^n\) 项），所以可以考虑使用位运算。

看看 \(E'_f\) 的每一项（\(O'_f\) 同理）：

\(E'_f = f_0x^0 + f_2x^1 + f_4x^2 + f_6x^3 + \cdots + f_{2^n-2}x^{2^{n-1}-1}\)

发现都是二进制中第 \(0\) 位为 \(0\) 的数

我们把 \(E'_f\) 和 \(O'_f\) 合并相当于把两个 \(2^{n-1}\) 项的数组合并，这样我们 \(\tt DP\) 地去做，定义 \(f_{i,s,j}\) 代表将两个 \(2^{i-1}\) 项式合并，这两个区间是 \([s, s+2^{i-1})\) 和 \([s+2^{i-1},s+2^i)\) 合并后 \(\omega_{2^i}^{j-s}\) 的结果。

发现 \(s\) 的个数 \(\times\) \(2^i\) 的个数是 \(O(n)\) 的，而 \(j\) 的个数是 \(O(2^i)\) 的，于是可以进行下一步复杂度分析
复杂度分析

对于递归版：

\(T(n) = 2T(\dfrac n2)+O(n) = O(n \log n)\)

证明：\(T(n) = O(n) + 2T(\dfrac n2) = O(n) + O(n) + 4T(\dfrac n4) = \cdots(\text{这个递归会有 log n 层})\cdots = \sum\limits^{\log n}_{i=0} O(n) = O(n \log n)\)

对于递推版：

\(T(n) = \sum\limits_{i=1}^{\log n} \sum\limits_{s=1}^{\frac n{2^i}} O(2^i) = \sum\limits_{i=1}^{\log n} O(\dfrac n{2^i} \times 2^i) = \sum\limits_{i=1}^{\log n} O(n) = O(n \log n)\)

3.IFFT

IDFT 公式推导

还记得我们在开篇提到的那个柿子吗：

\(\mathscr{F}^{-1} f = \frac{1}{\deg f+1} \sum_{k=0}^{\deg f} { f}_k {\omega}^{k}_{\deg f}\)

它的推导方法如下：

定义 \(\bar f(x) = \sum_{i} (\mathscr{F} f)_i x^i\)

然后再对 \(\bar f\) 做一次 DFT（lhx 内心吐槽：这方法是给人想的吗，个人感觉 \(\bar f\) 在数学上没什么实际意义，还来给 \(\bar f\) DFT？are you crazy???）

设 \(N = \deg f + 1\)（注意和 \(n = \log_2 (N)\) 做区别）

\(\bar f(\omega_N^x) = \sum\limits_{i=0}^{N-1} (\omega_N^{-xi} (\mathscr{F}f)_i) = \sum\limits_{i=0}^{N-1} (\omega_N^{-xi} \sum\limits_{j=0}^{N-1} f_j \omega_N^{ij})\)，粗体部分由于负负得正。

因为 \(\omega_N^{-xi}\) 相对 \(\sum\limits_{j=0}^{N-1} f_j \omega_N^{ij}\) 是常数，所以可以乘进去，也就是 \(\sum\limits_{i=0}^{N-1} \sum\limits_{j=0}^{N-1} f_j \omega_N^{-xi} \omega_N^{ij} = \sum\limits_{i=0}^{N-1} \sum\limits_{j=0}^{N-1} f_j ( \omega_N^i)^{j-x}\)

交换两个 \(\sum\)，并把 \(f_j\) 提出去，得到 \(\sum\limits_{j=0}^{N-1} \left ( f_j \sum\limits_{i=0}^{N-1} ( \omega_N^i)^{j-x} \right ) = \sum\limits_{j=0}^{N-1} \left ( f_j \sum\limits_{i=0}^{N-1} ( \omega_N^{j-x})^i \right )\)

这里 \(\sum\limits_{i=0}^{N-1} ( \omega_N^{j-x})^i\) 是一个等比数列，套用等比数列求和公式得到 \(\dfrac{1 - \omega_N^{(j-x)N}}{1 - \omega_N^{j-x}} = \dfrac{1 - 1}{1 - \omega_N^{j-x}} = 0\)，但是有一个条件，就是 \(\omega_N^{j-x} \ne 1\)，如果 \(\omega_N^{j-x} = 1\)，则答案为 \(n\)，于是我们得到 \(\sum\limits_{j=0}^{N-1} [j \equiv x \pmod N]N \times f_j = f_x \times N\)，于是我们得到一个离谱的结论：IFFT 就是先将单位根取倒数的 FFT。
实现

定理 1.1 \(\omega_N^a = \omega_N^{n \bmod N}\)

证明：\(\omega_N^a = \omega_N^{\lfloor a/N\rfloor N+a \bmod N}=\omega_N^{\lfloor a/N\rfloor N}\omega_{N}^{n \bmod N} = (\omega_N^N)^{\lfloor a/N\rfloor} \omega_{N}^{n \bmod N} = 1^{\lfloor a/N\rfloor} \omega_{N}^{n \bmod N} = \omega_{N}^{n \bmod N}\)

定理 1.2 \(\omega_N^{-a} = (\omega_N^{a})^{-1}\)

证明：\(\omega_N^{-a} = \omega_N^{(-a) \bmod N} = \omega_N^{N-a} = e^{i\pi\frac{2(N-a)}{N}} = e^{i\pi\frac{2N-2a}{N}} = e^{\frac{i\pi2N}{N}-\frac{i2\pi a}{N}} = e^{2\pi i} \div e^{2\pi i \times \frac aN} = (\omega_N^{a})^{-1}\)

于是我们可以通过 FFT 时 \(-a\) 改成 \(a\) 即可，或者说，\(Ia\)，其中 \(I=-1\) 代表 FFT，\(I=1\) 代表 IFFT。
应用

\(O(n \log n)\) \(\bmod x^N\) 多项式乘除法：

因为点值表示法可以直积/直商，所以先对两个多项式 FFT，直积/直商后 IFFT 回去就可以。

4.NTT

定义 \(\delta_p x(p \perp x) = \min\{i:x^i \bmod p = 1\}\)。

因为 \(x^{\varphi(p)} \bmod p=1(p \perp x)\)，所以 \(\delta_p x \le \varphi(i)\)。

那么，有一些整数，满足 \(\delta_p x = \varphi(i)\)，这种 \(x\) 就被称为是 \(p\) 的原根（可能不唯一）。

经常进行 NTT 的模数为 \(P=998244353=119 \cdot 2^{23}+1\)，其原根为 \(g=3\)。

令 \(q = 119\)，\(r = 23\)，以下同余式若未标明模数默认为 \(P\)。

有 \(P-1=q2^r\)，又因为长度经常为 \(N = \deg f+1 = 2^n\)，所以两边除上一个 \(2^n\)，得到 \(\dfrac {P-1}N = q2^{r-n}\)

令 \(q' = q2^{r-n}\)，令 \(\rho_N \equiv g^{q'}\)，发现 \(\omega_N\) 和 \(\rho_N\) 具有同样的性质，或者说 \(\langle \{0 \le i< n\mid\omega^i\},\times \rangle\) 和 \(\langle \{0 \le i < n\mid\omega^i\},\overset\bmod\times \rangle\) 这两个群同构。

Lemma 1: \(\rho_N^{i}\) 两两不同（证明：由于原根的性质，所以 \(\rho_N^i \equiv \rho_N^j \iff g^{q'i} \equiv g^{q'j} \iff q'i \equiv q'j \pmod {P-1} \iff (P-1) \mid q' (i-j)\)。

证明：构造双射 \(f(\omega_N^x) = \rho_N^x\)，有 \(f(\omega_N^x) f(\omega_N^y) = \rho_N^x \times \rho_N^y = \rho^{(x+y) \bmod N} = f(\omega_N^{(x+y) \bmod N}) = f(\omega_N^x\omega_N^y)\)

5.卷积

6.Misc（多项式全家桶）

\(\aleph_0\). 例题讲解

P3803

题意简述：给定多项式 \(f(x),g(x)\)，求 \(h(x) = f(x)g(x)\)。

讲解：就是个板子发现 \(h(x)\) 的定义式 \(f(x)g(x)\) 恰好是点值乘法，于是将 \(f,g\) FFT 然后乘起来 IFFT 回去就行了。

P1919

题意简述：给定大整数 \(x,y \le 10^{10^6}\)，求 \(z = xy\)。

讲解：也是个板子将大整数拆位当作多项式处理，此时得到的 \(Z(x) = X(x)Y(x)\) 会满足 \(Z(10) = xy\)，但是我们不能直接算 \(Z(10)\)，不然直接 \(\log^2 (x+y)\) 爆掉。于是考虑把进位一位一位传上去，这样复杂度可以接受。

P3338

题意简述：

给出 \(n\) 个实数 \(q_1,q_2, \dots q_n\)，求对于每一个 \(j\)，

\[\sum_{i = 1}^{j - 1} \frac{q_j}{(i - j)^2}-\sum_{i = j + 1}^{n} \frac{q_j}{(i - j)^2}
\]

，考虑凑成乘法形式