BZOJ1007: [HNOI2008]水平可见直线(单调栈)

Time Limit: 1 Sec  Memory Limit: 162 MB
Submit: 8638  Solved: 3327
[Submit][Status][Discuss]

Description

　　在xoy直角坐标平面上有n条直线L1,L2,...Ln,若在y值为正无穷大处往下看,能见到Li的某个子线段,则称Li为
可见的,否则Li为被覆盖的.
例如,对于直线:
L1:y=x; L2:y=-x; L3:y=0
则L1和L2是可见的,L3是被覆盖的.
给出n条直线,表示成y=Ax+B的形式(|A|,|B|<=500000),且n条直线两两不重合.求出所有可见的直线.

Input

　　第一行为N(0 < N < 50000),接下来的N行输入Ai,Bi

Output

　　从小到大输出可见直线的编号，两两中间用空格隔开,最后一个数字后面也必须有个空格

Sample Input

3
-1 0
1 0
0 0

Sample Output

1 2

HINT

 

Source

我的思路：

对于一条直线，如果看不见，有且仅有两种情况

一：被一条斜率相同，但是$b$比它大的直线遮挡住

二：被两条交叉的直线遮挡住，也就是下面这种情况

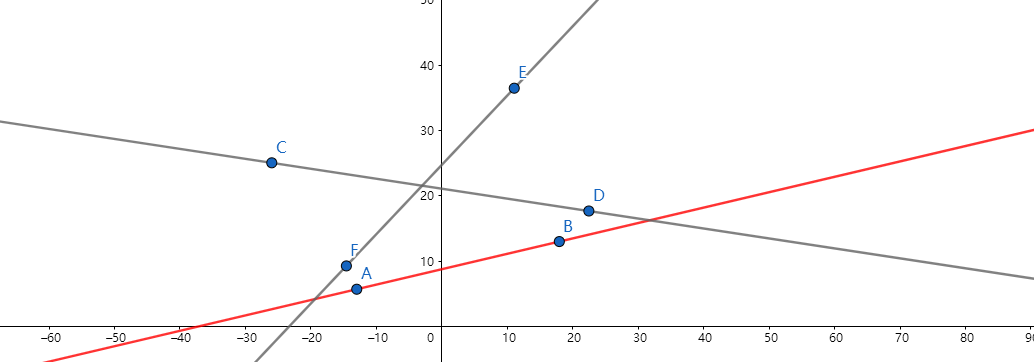
对于第一种情况，直接判断即可

对于第二种情况，直接处理有一些麻烦，所以我们考虑首先按照斜率从小到大排序

同时维护一个栈

如果当前直线与栈顶元素的前一个元素的交点 比 栈顶元素和栈顶前一个元素的交点 的横坐标 靠左，那么栈顶的前一个元素就没用了

最后统计栈中有哪些元素就可以

有点类似于单调栈

时间复杂度:$O(n)$

#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
const int MAXN = ;
const double eps = 1e-;
inline int read() {
    char c = getchar(); int x = , f = ;
    while(c < '' || c > '') {if(c == '-') f = -;c = getchar();}
    while(c >= '' && c <= '') {x = x *  + c - '';c = getchar();}
    return x * f;
}
int N;
struct Seg {
    int ID;
    double k, b;
    bool operator < (const Seg &rhs) const {
        return fabs(k - rhs.k) <= eps ? b < rhs.b : k < rhs.k;
    }
}a[MAXN], S[MAXN];
int top = ;
int Ans[MAXN];
double X(Seg x, Seg y) {
    return (y.b - x.b) / (x.k - y.k);
}
void Solve() {
    fill(Ans + , Ans + N + , );
    S[++top] = a[];
    for(int i = ; i <= N; i++) {
        while( ( fabs(a[i].k - S[top].k) <= eps)
            || (top >  && X(a[i], S[top - ]) <= X(S[top - ], S[top])))
            Ans[S[top].ID] = , top--;
        S[++top] = a[i];
    }
}
int main() {
    #ifdef WIN32
    freopen("a.in","r",stdin);
    #else
    //freopen("bzoj_1007.in","r",stdin);
    //freopen("bzoj_1007.out","w",stdout);
    #endif
    N = read();
    for(int i = ; i <= N; i++)
        a[i].k = read(), a[i].b = read(), a[i].ID = i;
    sort(a + , a + N + );
    Solve();
    for(int i = ; i <= N; i++)
        if(Ans[i] == )
            printf("%d ",i);
    return ;
}