平衡树splay学习笔记#2

讲一下另外的所有操作（指的是普通平衡树中的其他操作）

前一篇的学习笔记连接：【传送门】，结尾会带上完整的代码。

---

操作1，pushup操作

之前学习过线段树，都知道子节点的信息需要更新到父亲节点上。
因为旋转之后有两个节点的儿子和两个节点的父亲被改变了，那么原来的总儿子个数也就是sz就被改变了。
那么我们需要维护sz，就需要pushup操作。
这个东西比较简单。

void pushup(int nod) {
    tr[nod].sz = tr[tr[nod].ch[0]].sz + tr[tr[nod].ch[1]].sz + tr[nod].cnt;
}

---

操作2，插入操作(insert)

上一次的博客已经讲过了，如果有相同权值的节点，那么就放到一个相同的节点内，将cnt个数+1，如果没有那么就新开一个。
insert操作就是这样实现的。
请看如下的图片：

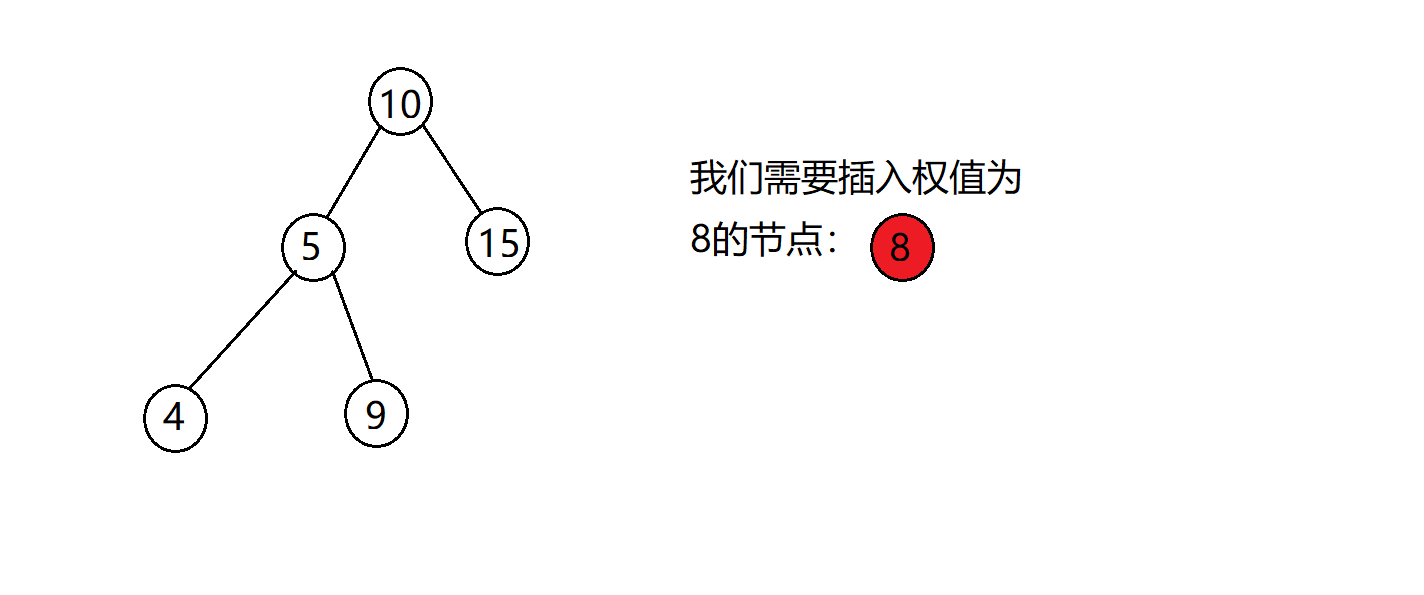
我们要讲这个权值为8的节点插入到BST中，根据BST的原则，不能有重复的节点，但是在这里不存在。

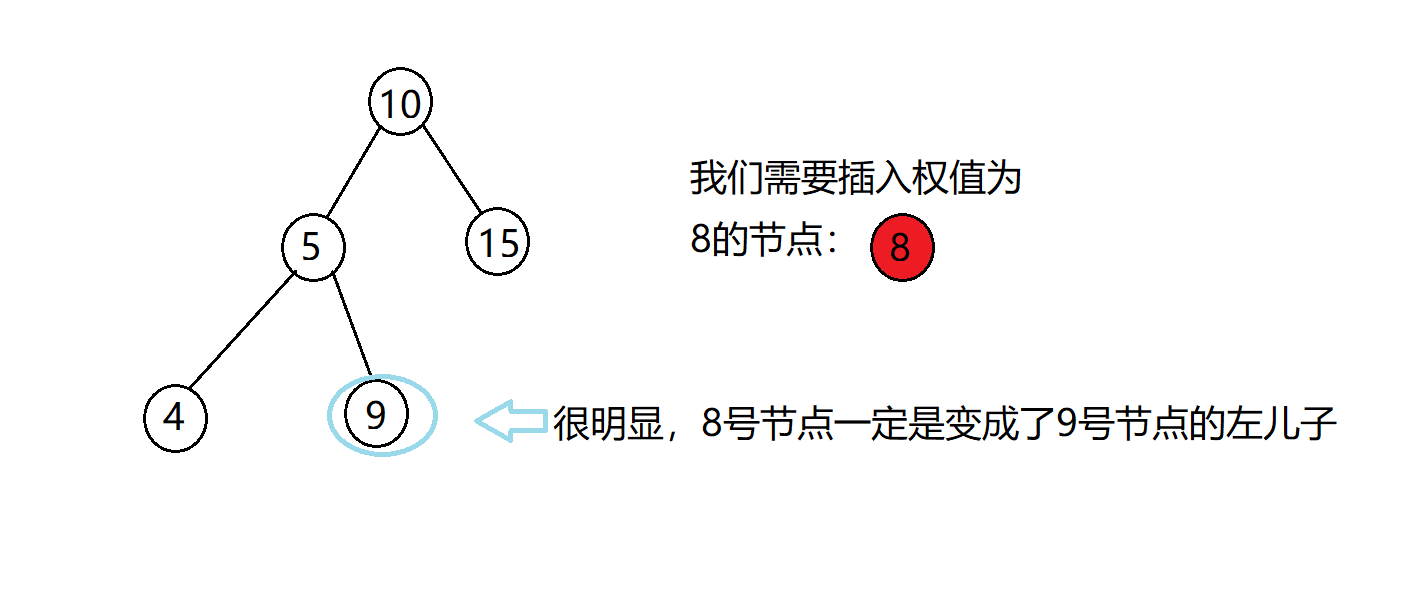
很明显这个8一定是变成了权值为9的节点的左儿子，因为他比5要大，但是比9要小。
那么我们就可以像二分查找一样的思路，找到9的位置。如果当前的节点权值比插入的权值大，那么就到节点的左节点查找，反之到右节点，这也是后面查找的原理。

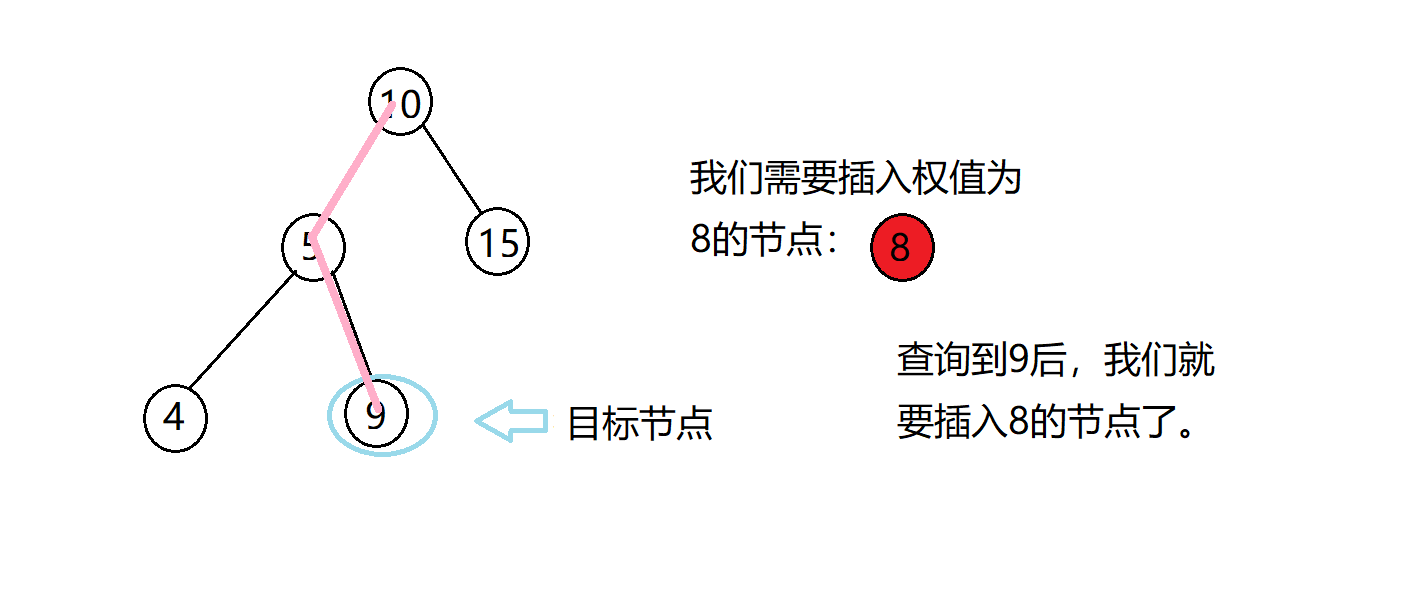
上图粉色的线就是我们查找的路径。

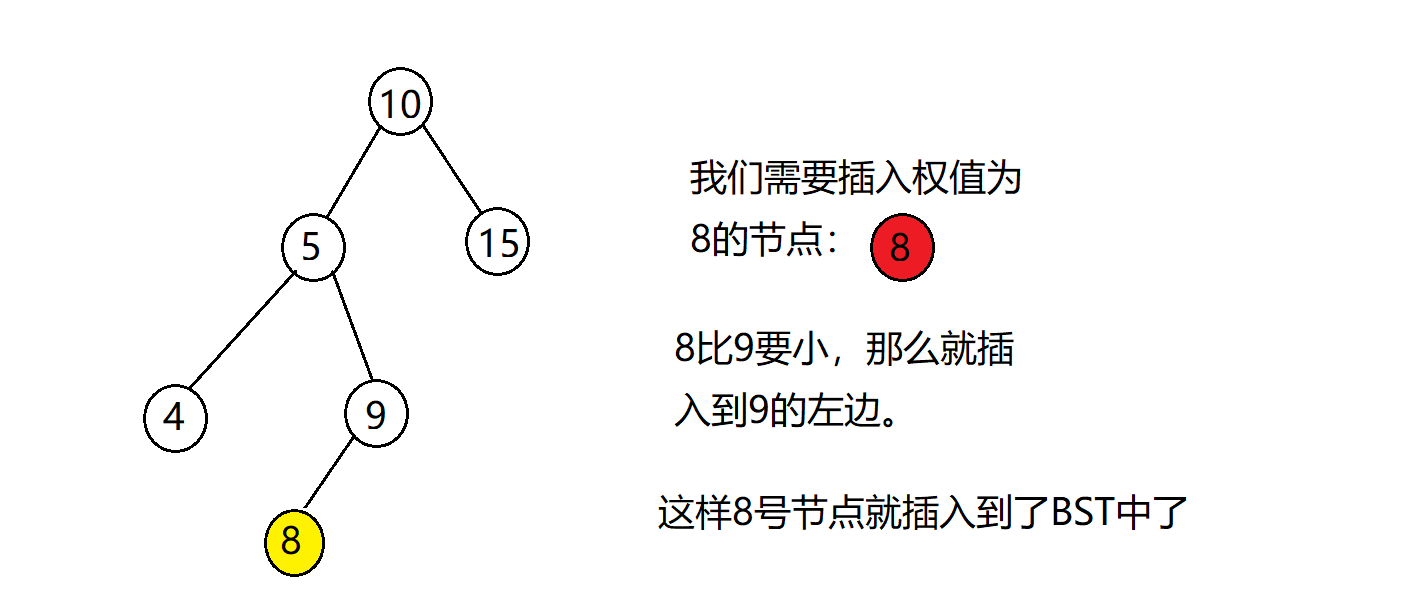
插入节点后我们会发现，那条链又出来了，我们就开始splay操作，将这个u转到根节点的位置，来改变树的形状。

void ins(int x) {
    int u = rt, ft = 0;//u表示当前的节点，ft表示u的父亲，因为我们需要更新父亲的子节点。
    while (u && tr[u].val != x) {//如果u不是空的节点，而且没有找到相同权值的节点，那么就继续向下查找
        ft = u;//记录父亲
        u = tr[u].ch[x > tr[u].val];//x>tr[u].val时，那么就是1也就是跳到右儿子，否则是跳到左儿子。
    }
    if (u) tr[u].cnt ++;//如果有相同的权值的节点，那么就在cnt上标记2+1
    else {
        u = ++ tot;//就新加一个节点
        if (ft) tr[ft].ch[x > tr[ft].val] = u;//如果这个节点是根节点，那么就没有必要更新父亲节地了。
        tr[u].init(x, ft);//插入节点的所有信息
    }
    splay(u, 0);//将节点
}

---

操作3，查询操作，find

上面稍微提到了一点点，类似于二分查找，不过只是在树上，而且已经满足了BST的性质了。
分两种情况讨论

• 如果当前节点的权值>查询的值，那么说明这个节点可能在左子树中，那么查询左子树
• 如果当前节点的权值<查询的值，那么说明这个节点可能在右子树中，那么查询右子树

为了方便我们接下来的操作和直接调用查询，那么我们就选择了把这个节点旋转根节点的位置。
因为和二分查找差不多，所以时间复杂度差不多就是logn。

void find(int x)  {
    int u = rt;
    if (!u) return;//如果是空的，那么就跳过。
    while (tr[u].ch[x > tr[u].val] && x != tr[u].val) {//如果没有找到或者是没有走到底部
        u = tr[u].ch[x > tr[u].val];//x>tr[u].val时，那么就是1也就是跳到右儿子，否则是跳到左儿子。
    }
    splay(u, 0);//旋转到根节点
}

---

操作4，查找前驱和后继

理解了find操作后应该也能理解前驱和后继。
所谓前驱就是小于它的最大的数，后继就是大于它的最小的数。
那么严格前驱和严格后继就是不存在相同的情况。
首先是前驱，前驱是小于它的数，那么一定是在当前节点的左子树中。
这个时候我们的旋转到根节点的操作就派上用场了，因为根节点就是我们需要查找的节点，所以可以直接操作。
然后以为是最大的数，那么也就是在左子树中一直往右儿子边走。
那么同理后继就是在右子树中一种往左儿子走。是不是特别好理解。
如果还是不理解的话，我下次考虑画一个图，这样更加清晰。
yyb巨佬喜欢吧前驱和和后继写到一起，但是我更喜欢分开来写，虽然代码长了一点，但是更加清楚

int pre(int x)  {//前驱
    find(x);
    int u = rt;
    if (tr[u].val < x) return u;//如果根节点的答案就是小于的，那么就直接输出。
    u = tr[u].ch[0];//到左子树中
    while (tr[u].ch[1]) u = tr[u].ch[1];//一直往右儿子边走
    return u;
}
int suc(int x) {
    find(x);
    int u = rt;
    if (tr[u].val > x) return u;//如果根节点的答案就是大于的，那么就直接输出。
    u = tr[u].ch[1];//到右子树中
    while (tr[u].ch[0]) u = tr[u].ch[0];//一直往左儿子走
    return u;
}

---

操作5，删除操作（delete）

现在就很简单啦
首先找到这个数的前驱，把他Splay到根节点
然后找到这个数后继，把他旋转到前驱的底下
比前驱大的数是后继，在右子树
比后继小的且比前驱大的有且仅有当前数
在后继的左子树上面，
因此直接把当前根节点的右儿子的左儿子删掉就可以啦

void del(int x) {
    int lst = pre(x), nxt = suc(x);//查找前驱和后继
    splay(lst, 0); //将lst转到根节点
    splay(nxt, lst);//将nxt转到lst的位置。
    int del = tr[nxt].ch[0];//那么删除的数就是nxt的左儿子
    if (tr[del].cnt > 1) {//如果原来就>1个，那么直接-1
        tr[del].cnt --;
        splay(del, 0);
    }
    else tr[nxt].ch[0] = 0;//不然直接删除
}

---

操作6，查找第k大(kth)

这个也非常简单。
如果当前节点的左子树+节点cnt还是小于k，那么说明在右子树
k-=上面所说的和，查找右子树
如果左子树的节点个数足够，那么就查找左子树
否则一定是在当前的根节点，直接输出根节点。

int kth(int x) {
    int u = rt;
    if (tr[u].sz < x) return 0;//如果不存在x个，那么就输出0
    while (1) {
        int lc = tr[u].ch[0];//左儿子
        if (x > tr[lc].sz + tr[u].cnt) {//情况1
            x -= tr[lc].sz + tr[u].cnt;
            u = tr[u].ch[1];//跳右儿子
        }
        else {
            if (tr[lc].sz >= x) u = lc;//如果左儿子节点的个数足够，那么就到左儿子上面查找
            else return tr[u].val;//不然就是在当前的节点上
        }
    }
}

---

结尾AC完整代码

#include <bits/stdc++.h>
#define N 100005
#define inf 2147483647
using namespace std;
template <typename T>
inline void read(T &x) {
    x = 0; T fl = 1;
    char ch = 0;
    while (ch < '0' || ch > '9') {
        if (ch == '-') fl = -1;
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9') {
        x = (x << 1) + (x << 3) + (ch ^ 48);
        ch = getchar();
    }
    x *= fl;
}
struct Splay {
    int rt, tot;
    struct node {
        int val, fa, cnt, sz, ch[2];
        void init(int x, int ft) {
            fa = ft;
            val = x;
            ch[1] = ch[0] = 0;
            sz = cnt = 1;
        }
    }tr[N];
    Splay() {
        memset(tr, 0, sizeof(tr));
        rt = tot = 0;
    }
    void pushup(int nod) {
        tr[nod].sz = tr[tr[nod].ch[0]].sz + tr[tr[nod].ch[1]].sz + tr[nod].cnt;
    }
    void rotate(int nod) {
        int fa = tr[nod].fa, gf = tr[fa].fa, k = tr[fa].ch[1] == nod;
        tr[gf].ch[tr[gf].ch[1] == fa] = nod;
        tr[nod].fa = gf;
        tr[fa].ch[k] = tr[nod].ch[k ^ 1];
        tr[tr[nod].ch[k ^ 1]].fa = fa;
        tr[nod].ch[k ^ 1] = fa;
        tr[fa].fa = nod;
        pushup(fa);
        pushup(nod);
    }
    void splay(int nod, int goal) {
        while (tr[nod].fa != goal) {
            int fa = tr[nod].fa, gf = tr[fa].fa;
            if (gf != goal) {
                if ((tr[gf].ch[0] == fa) ^ (tr[fa].ch[0] == nod)) rotate(nod);
                else rotate(fa);
            }
            rotate(nod);
        }
        if (goal == 0) rt = nod;
    }
    void find(int x)  {
        int u = rt;
        if (!u) return;//如果是空的，那么就跳过。
        while (tr[u].ch[x > tr[u].val] && x != tr[u].val) {//如果没有找到或者是没有走到底部
            u = tr[u].ch[x > tr[u].val];//x>tr[u].val时，那么就是1也就是跳到右儿子，否则是跳到左儿子。
        }
        splay(u, 0);//旋转到根节点
    }
    void ins(int x) {
        int u = rt, ft = 0;//u表示当前的节点，ft表示u的父亲，因为我们需要更新父亲的子节点。
        while (u && tr[u].val != x) {//如果u不是空的节点，而且没有找到相同权值的节点，那么就继续向下查找
            ft = u;//记录父亲
            u = tr[u].ch[x > tr[u].val];//x>tr[u].val时，那么就是1也就是跳到右儿子，否则是跳到左儿子。
        }
        if (u) tr[u].cnt ++;//如果有相同的权值的节点，那么就在cnt上标记2+1
        else {
            u = ++ tot;//就新加一个节点
            if (ft) tr[ft].ch[x > tr[ft].val] = u;//如果这个节点是根节点，那么就没有必要更新父亲节地了。
            tr[u].init(x, ft);//插入节点的所有信息
        }
        splay(u, 0);//将节点
    }
    int pre(int x)  {
        find(x);
        int u = rt;
        if (tr[u].val < x) return u;//如果根节点的答案就是小于的，那么就直接输出。
        u = tr[u].ch[0];//到左子树中
        while (tr[u].ch[1]) u = tr[u].ch[1];//一直往右儿子边走
        return u;
    }
    int suc(int x) {
        find(x);
        int u = rt;
        if (tr[u].val > x) return u;//如果根节点的答案就是大于的，那么就直接输出。
        u = tr[u].ch[1];//到右子树中
        while (tr[u].ch[0]) u = tr[u].ch[0];//一直往左儿子走
        return u;
    }
    void del(int x) {
        int lst = pre(x), nxt = suc(x);//查找前驱和后继
        splay(lst, 0); //将lst转到根节点
        splay(nxt, lst);//将nxt转到lst的位置。
        int del = tr[nxt].ch[0];//那么删除的数就是nxt的左儿子
        if (tr[del].cnt > 1) {//如果原来就>1个，那么直接-1
            tr[del].cnt --;
            splay(del, 0);
        }
        else tr[nxt].ch[0] = 0;//不然直接删除
    }
    int kth(int x) {
        int u = rt;
        if (tr[u].sz < x) return 0;//如果不存在x个，那么就输出0
        while (1) {
            int lc = tr[u].ch[0];//左儿子
            if (x > tr[lc].sz + tr[u].cnt) {//情况1
                x -= tr[lc].sz + tr[u].cnt;
                u = tr[u].ch[1];//跳右儿子
            }
            else {
                if (tr[lc].sz >= x) u = lc;//如果左儿子节点的个数足够，那么就到左儿子上面查找
                else return tr[u].val;//不然就是在当前的节点上
            }
        }
    }
}sl;
int main() {
    int n; read(n);
    sl.ins(-inf);
    sl.ins(inf);
    for (int _t = 1; _t <= n; _t ++) {
        int opt, x; read(opt); read(x);
        if (opt == 1) sl.ins(x);
        if (opt == 2) sl.del(x);
        if (opt == 3) {
            sl.find(x);
            printf("%d\n", sl.tr[sl.tr[sl.rt].ch[0]].sz);
        }
        if (opt == 4) printf("%d\n", sl.kth(x + 1));
        if (opt == 5) printf("%d\n", sl.tr[sl.pre(x)].val);
        if (opt == 6) printf("%d\n", sl.tr[sl.suc(x)].val);
    }
    return 0;
}