5. Longest Palindromic Substring(最长回文子串 manacher 算法/ DP动态规划)

Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.

Example:

Input: "babad"

Output: "bab"

Note: "aba" is also a valid answer.

Example:

Input: "cbbd"

Output: "bb"

manacher 算法

回文有奇数偶数的问题，所以加上gap,这样字符串一定是奇数,所以只考虑奇数匹配就行。

a b c -----> #a#b#c#

a b       -->#a#b#

1、预处理成上面的样子，为处理方便，在最前面加一个从未出现的字符$

2、建立数组P，P[i] 来记录字符S[i]为中心的最长回文子串向左/向右扩张的长度（包括S[i]）

例如：

12212321

预处理：$#1#2#2#1#2#3#2#1#

P: 12125214121612121

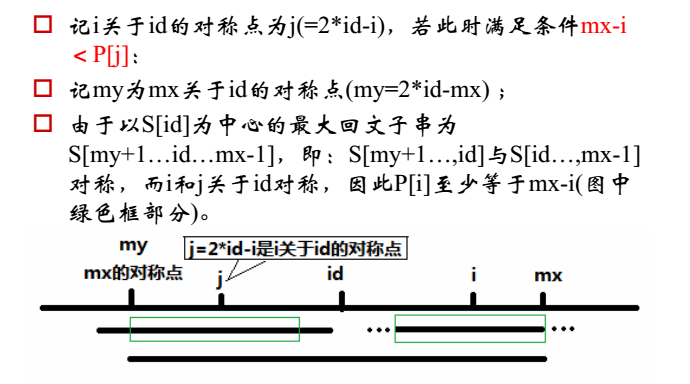
绿框之外的暴力

 class Solution:
     def longestPalindrome(self, s):
         """
         :type s: str
         :rtype: str
         """
         # preprocess
         slist = list(s)
         for i in range((len(s) + 1) * 2)[::2]:
             slist.insert(i, "#")
         slist.insert(0, '$')

         p = self.manacher(slist)

         i = p.index(max(p))
         ans = ''.join(slist[i-p[i]+1:i+p[i]])
         return ans.replace('#','').replace('$','')
     def manacher(self, slist):

         # 计算p
         p = [0] * len(slist)
         p[0] = 1
         id = 0
         mx = 1
         print(slist)
         for i in range(1,len(slist)):
             if mx > i:
                 p[i] = min(p[id * 2 - i], mx - i)
             else:
                 p[i] = 1

             #暴力
             while i +p[i]<len(slist) and slist[i - p[i]]==slist[i + p[i]]:
                 p[i] = p[i]+1
             #更新最大三元组
             if(mx < i + p[i]):
                 mx = i + p[i]
                 id = i

         return p

动态规划

此题还可以用动态规划Dynamic Programming来解，我们维护一个二维数组dp，其中dp[i][j]表示字符串区间[i, j]是否为回文串，当i = j时，只有一个字符，肯定是回文串，如果i = j + 1，说明是相邻字符，此时需要判断s[i]是否等于s[j]，如果i和j不相邻，即i - j >= 2时，除了判断s[i]和s[j]相等之外，dp[j + 1][i - 1]若为真，就是回文串，通过以上分析，可以写出递推式如下：

dp[i, j] = 1                                               if i == j

= s[i] == s[j]                                if j = i + 1

= s[i] == s[j] && dp[i + 1][j - 1]    if j > i + 1

中心扩散法：