猫映射（Arnold变换），猫脸变换介绍与基于例题脚本的爆破

前置信息

http://www.jiamisoft.com/blog/index.php/7249-erzhituxiangjiamisuanfaarnold.html

https://mp.weixin.qq.com/s/IbkAlyAPvbgMeNgqfwisTg

Arnold变换

Arnold变换是V.J．Arnold在遍历理论的研究中提出的一种变换，原意为catmapping，俗称猫脸变换。Arnold变换直观、简单、具有周期性，使用非常方便。Arnold变换的原理是先作x轴方向的错切变换，再作y轴方向的错切变换，最后的模运算相当于切割回填操作。

当对图像进行Arnold变换时，就是把图像的各个像素点位置按照下列公式进行移动，

从而得到一个相对原图像比较混乱的图像。对图像每进行一次Arnold变换，就相当于对该图像进行了一次置乱，一般来说这一过程需要反复进行多次才能达到令人满意的效果。利用Arnold变换对图像进行置乱后，使原本有意义的图像变成了像白噪声一样无意义的图像，从而实现了信息的初步隐藏。同时置乱次数可以作为水印系统的密钥，从而进一步增强系统的安全性和保密性。

Arnold变换也是具有周期性的。F．J．Dyson和H.Falk在分析离散Arnold变换的周期性时，给出了这样的结论：对于任意的N>2，Arnold变换的周期L≤N2/2。这是迄今为止最好的结果。计算Arnold周期的方法，对于给定的自然数N>2，下式的Arnold变换周期M是使得它成立的最小自然数n。

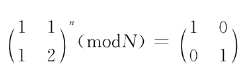
反变换查看原文，就不多赘述了

基于pillow库的加密实现

from PIL import Image
def arnold(infile: str, outfile: str = None, a: int = 1, b: int = 1, shuffle_times: int = 1, reverse: bool = False) -> None:
"""
Arnold猫脸变换函数
    Parameters:
infile - 输入图像路径
outfile - 输出图像路径
a - Anrold 变换参数
b - Anrold 变换参数
shuffle_times - 置乱次数
reverse - 逆变换
"""
inimg = Image.open(infile)
width, height = inimg.size
indata = inimg.load()
outimg = Image.new(inimg.mode, inimg.size)
outdata = outimg.load()
    for _ in range(shuffle_times):
        for x in range(width):
           for y in range(height):
                 if reverse:
                      nx = ((a * b + 1) * x - a * y) % width
                      ny = (y - b * x) % height
                 else:
                      nx = (x + a * y) % width
                      ny = (b * x + (a * b + 1) * y) % height
                     outdata[ny, nx] = indata[y, x]
            outimg.save(outfile if outfile else "arnold_"+infile, inimg.format)
arnold("before.png", "encode.png", 9, 39, 1)
arnold("encode.png", "decode.png", 9, 39, 1, True)

2024鹏程杯

import numpy as np
import cv2

def arnold_decode(image, arnold_times):
    a = 7
    b = 35
    # 创建新的解码图像，初始化为全0，数据类型为uint8
    decode_image = np.zeros(shape=image.shape, dtype=np.uint8)
    height, width = image.shape[0], image.shape[1]
    N = height  # N是正方形的边长
    for _ in range(arnold_times):  # 进行arnold_times次变换
        for old_x in range(height):
            for old_y in range(width):
                # 计算新的像素坐标
                new_x = ((a * b + 1) * old_x + (-a) * old_y) % N
                new_y = ((-b) * old_x + old_y) % N
                decode_image[new_x, new_y, :] = image[old_x, old_y, :]
    # 保存解码后的图像，确保图像保存成功
    try:
        cv2.imwrite('flag.png', decode_image, [int(cv2.IMWRITE_PNG_COMPRESSION), 0])  # 以PNG格式保存图像
        print("解码图像已保存为 flag.png")
    except Exception as e:
        print(f"保存图像时发生错误: {e}")
    return decode_image

if __name__ == '__main__':
    # 读取图像并确保图像加载成功
    image = cv2.imread('4.jpg')
    if image is not None:
        arnold_decode(image, 1)  # 此处arnold_times设置为1
    else:
        print("图像加载失败，请检查文件路径。")

2024源鲁杯CTFMisc

    image = np.array(image)
    arnold_image = np.zeros(shape=image.shape, dtype=image.dtype)
    h, w = image.shape[0], image.shape[1]
    N = h
    for _ in range(shuffle_times):
        for ori_x in range(h):
            for ori_y in range(w):
                new_x = (1*ori_x + b*ori_y)% N
                new_y = (a*ori_x + (a*b+1)*ori_y) % N
                if mode == '1':
                    arnold_image[new_x, new_y] = image[ori_x, ori_y]
                else:
                    arnold_image[new_x, new_y, :] = image[ori_x, ori_y, :]
    return Image.fromarray(arnold_image)

import numpy as np
from PIL import Image

def arnold_decode(image, shuffle_times=10, a=1, b=1, mode='1'):
    image = np.array(image)
    decode_image = np.zeros(shape=image.shape, dtype=image.dtype)
    h, w = image.shape[0], image.shape[1]
    N = h
    for _ in range(shuffle_times):
        for ori_x in range(h):
            for ori_y in range(w):
                new_x = ((a*b+1)*ori_x + (-b)* ori_y)% N
                new_y = ((-a)*ori_x + ori_y) % N
                if mode == '1':
                    decode_image[new_x, new_y] = image[ori_x, ori_y]
                else:
                    decode_image[new_x, new_y, :] = image[ori_x, ori_y, :]
    return Image.fromarray(decode_image)

img = Image.open('flag.png')
decode_img = arnold_decode(img)
decode_img.save('flag-output.png')

2024源鲁杯CTFCrypto

import matplotlib.pyplot as plt
import cv2
import numpy as np
from PIL import Image
def de_arnold(img,shuffle_time,a,b):
    r, c, d = img.shape
    dp = np.zeros(img.shape, np.uint8)

    for s in range(shuffle_time):
        for i in range(r):
            for j in range(c):
                x = ((a * b + 1) * i - b * j) % r
                y = (-a * i + j) % c
                dp[x, y, :] = img[i, j, :]
        img = np.copy(dp)
    cv2.imwrite(f"flag.png",img)

img_en = cv2.imread('en_flag.png')
de_arnold(img_en, 3,6, 9)

0xGame2024Misc

from PIL import Image
​
img = Image.open('mijiha.png')
if img.mode == "P":
    img = img.convert("RGB")
assert img.size[0] == img.size[1]
dim = width, height = img.size
​
st = 1
a = 35
b = 7
for _ in range(st):
    with Image.new(img.mode, dim) as canvas:
        for nx in range(img.size[0]):
            for ny in range(img.size[0]):
                y = (ny - nx * a) % width
                x = (nx - y * b) % height
                canvas.putpixel((y, x), img.getpixel((ny, nx)))
canvas.show()
canvas.save('flag.png')

了解这些比赛例题解密代码后

如果只知道啊a,b不知道翻转次数

那我们只有一个办法，爆破。

这是基于理解修改的一个爆破脚本

import os
import cv2
import numpy as np

def de_arnold(img, shuffle_time, a, b):
    r, c, d = img.shape
    dp = np.zeros(img.shape, np.uint8)

    for s in range(shuffle_time):
        for i in range(r):
            for j in range(c):
                x = ((a * b + 1) * i - b * j) % r
                y = (-a * i + j) % c
                dp[x, y, :] = img[i, j, :]
        img = np.copy(dp)
    return img

# 参数设置
a, b = ?,  ? # Arnold变换的参数
max_attempts = ? # 爆破的最大尝试次数
output_dir = "decrypted_images"  # 输出文件夹
os.makedirs(output_dir, exist_ok=True)

# 读取加密图片
img_en = cv2.imread('en_flag.png')
if img_en is None:
    raise FileNotFoundError("加密图片未找到，请检查路径和文件名是否正确。")

# 开始爆破
for shuffle_time in range(1, max_attempts + 1):
    img_decrypted = de_arnold(img_en, shuffle_time, a, b)
    output_path = os.path.join(output_dir, f"flag_{shuffle_time}.png")
    cv2.imwrite(output_path, img_decrypted)
    print(f"解密图片已保存: {output_path}")

print(f"爆破完成，共生成 {max_attempts} 张解密图片，保存在文件夹: {output_dir}")

题目一个数据没给，我们可以直接对3个未知量直接进行爆破，注意一下能爆破说明数值不是很大

import matplotlib.pyplot as plt
import cv2
import numpy as np

def arnold_decode(image, shuffle_times, a, b):
    """ decode for rgb image that encoded by Arnold
    Args:
        image: rgb image encoded by Arnold
        shuffle_times: how many times to shuffle
    Returns:
        decode image
    """
    # 1:创建新图像
    decode_image = np.zeros(shape=image.shape)
    # 2：计算N
    h, w = image.shape[0], image.shape[1]
    N = h  # 或N=w

    # 3：遍历像素坐标变换
    for time in range(shuffle_times):
        for ori_x in range(h):
            for ori_y in range(w):
                # 按照公式坐标变换
                new_x = ((a * b + 1) * ori_x + (-b) * ori_y) % N
                new_y = ((-a) * ori_x + ori_y) % N
                decode_image[new_x, new_y, :] = image[ori_x, ori_y, :]
        image = np.copy(decode_image)

    return image

def arnold_brute(image,shuffle_times_range,a_range,b_range):
    for c in range(shuffle_times_range[0],shuffle_times_range[1]):
        for a in range(a_range[0],a_range[1]):
            for b in range(b_range[0],b_range[1]):
                print(f"[+] Trying shuffle_times={c} a={a} b={b}")
                decoded_img = arnold_decode(image,c,a,b)
                output_filename = f"flag_decodedc{c}_a{a}_b{b}.png"
                cv2.imwrite(output_filename, decoded_img, [int(cv2.IMWRITE_PNG_COMPRESSION), 0])

if __name__ == "__main__":
    img = cv2.imread("cat.png")
    arnold_brute(img, (1,8), (1,12), (1,12))

这样我们就可以得到原图