CF629E Famil Door and Roads【树上计数+分类讨论】

Online Judge：Codeforces629E，Luogu-CF629E

Label：树上计数，分类讨论，换根

题目描述

给出一棵n个节点的树。有m个询问，每一个询问包含两个数a、b，我们可以对任意两个不相连的点连一条无向边，并且使得加上这条边后a，b处在一个环内。对于每一个询问，求这样的环的期望长度。

\(2<=n,m<=10^5\)

输入

第一行包括两个整数n，m，分别表示节点数和询问数。

接下来n-1行，每行两个整数u、v表示有一条从u到v的边。

接下来m行，每行两个整数a、b（a≠b），表示一个询问。

输出

对于每一个询问，输出满足条件的环的期望长度。答案保留6位小数。

样例

Input#1

4 3
2 4
4 1
3 2
3 1
2 3
4 1

Output#1

4.00000000
3.00000000
3.00000000

Input#2

3 3
1 2
1 3
1 2
1 3
2 3

Output#2

2.50000000
2.50000000
3.00000000

题解

题目求的是期望，其实就是求两个东西，\(all=\)能形成环的个数，\(ans=\)所有环的长度总和，两者相除得到答案。

转化为树上的计数问题。接下来分两种情况讨论。

先交代下面会用到的数组，及其意义。

\(sz[x]\)：以x为根的子树所含节点的个数。

\(dep[x]\)：节点深度。

\(fa[x][i=0..17]\)：x向上第\(2^i\)个祖先（供后面倍增跳LCA用）。

\(sum[x]\)：\(= ∑_{son∈x}dep[son]\)，也就是子树中所有点的深度之和。

\(tot[x]\)：后面再说。

1.(u,v)不是祖先关系

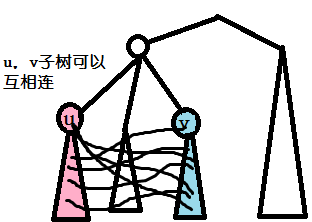
发现只能将u,v子树里的点连起来。

所以，能形成环的个数\(all=sz[u]*sz[v]\)，其中\(sz\)数组表示子树所含节点个数。

所有环的长度之和：

\[ans+=sz[u]*(sum[v]-dep[v]*sz[v]);\\ans+=sz[v]*(sum[u]-dep[u]*sz[u]);\\ans+=all*(dep[u]+dep[v]-2*dep[lca]+1);(lca是指u,v的LCA)
\]

根据图很容易理解。

---

2.(u,v)是祖先关系

特殊点说明：将深度小的点作为u。son是u的儿子中通向v的那一个。v是深度较大的那一个。

如何求son？倍增向上跳\(dep[v]-dep[u]-1\)步，可以在O(logN)时间内得到。

---

看下面这幅图，我们只能在v的子树中选一个点，在蓝色部分（除子树son的点）选一个点，将两者相连，才能形成环。

所以，环的个数\(all=sz[v]*(sz[1]-sz[son])\)。

如何求环的长度总和？分成下面几部分分步求解。

这里换个元方便下面表示\(sz1=sz[v]\)，\(sz2=(sz[1]-sz[son])\)。\(sz1\)就是粉色部分的点数，\(sz2\)就是蓝色部分的点数。

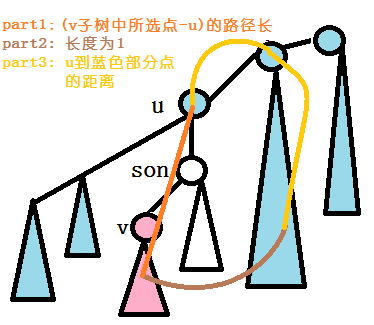
part1:

\(ans+=(sum[v]-dep[v]*sz1)*sz2+(dep[v]-dep[u])*all\)

part2:

\(ans+=1*all\)

part3：

这个东西与前面几个相比不太好分析。

求树上两点(a,b)的距离就是\(dep[a]+dep[b]-2*dep[LCA(a,b)]\)。

全部加起来，那么现在我们求的就是下面这东西。

\[dep[u]*sz2+∑_{x∈bluepart}(dep[x]-2*dep[LCA(u,x)])
\]

前面那个可以O(1)算出。就是后面那一坨如何在可行的时间内弄出？

考虑预处理一个数组\(tot[son]\)，表示，若它的父亲节点为u，则\(tot[son]=∑_{x∈bluepart}(dep[x]-2*dep[LCA(u,x)])\)也就是上面式子中后面的部分。

dfs一遍，完成\(tot\)数组的预处理，转移如下。画个图还是很好理解的，当弄到x时，f就是上式的lca。

void dfs2(int x){
    int f=fa[x][0];
    if(f){
        tot[x]=tot[f]+sum[f]-sum[x];
        tot[x]-=2ll*(sz[f]-sz[x])*dep[f];
    }
    for(int i=head[x];i;i=e[i].nxt)if(e[i].to!=fa[x][0])dfs2(e[i].to);
}

综上分两种情况讨论，时间复杂度为\(O(NlogN)\)。

完整代码如下：

//原题CF629E
#include<bits/stdc++.h>
#define int long long
using namespace std;
typedef long long ll;
const int N=1e5+10;
inline int read(){
    int x=0;char c=getchar();
    while(c<'0'||c>'9')c=getchar();
    while(c>='0'&&c<='9')x=(x<<3)+(x<<1)+(c^48),c=getchar();
    return x;
}
struct edge{
    int to,nxt;
}e[N<<1];
int head[N],ecnt;
inline void link(int u,int v){
    e[++ecnt].to=v,e[ecnt].nxt=head[u];
    head[u]=ecnt;
}
int n,m;
ll sum[N],tot[N];
int sz[N],dep[N],fa[N][18];
ll gcd(ll a,ll b){return b==0?a:gcd(b,a%b);}
void dfs(int x,int f){
    fa[x][0]=f,dep[x]=dep[f]+1,sum[x]=dep[x];
    sz[x]=1;
    for(int i=head[x];i;i=e[i].nxt){
        int y=e[i].to;if(y==f)continue;
        dfs(y,x);
        sz[x]+=sz[y];
        sum[x]+=sum[y];
    }
}
void dfs2(int x){
    int f=fa[x][0];
    if(f){
        tot[x]=tot[f]+sum[f]-sum[x];
        tot[x]-=2ll*(sz[f]-sz[x])*dep[f];
    }
    for(int i=head[x];i;i=e[i].nxt)if(e[i].to!=fa[x][0])dfs2(e[i].to);
}
inline int jump(int x,int stp){
    for(int i=0;i<=17;i++)if(stp&(1<<i))x=fa[x][i];
    return x;
}
inline int LCA(int x,int y){
    if(dep[x]<dep[y])swap(x,y);
    int stp=dep[x]-dep[y];
    x=jump(x,stp);
    if(x==y)return x;
    for(int i=17;i>=0;i--)if(fa[x][i]!=fa[y][i])x=fa[x][i],y=fa[y][i];
    return fa[x][0];
}
signed main(){
    n=read(),m=read();
    for(int i=1;i<n;i++){
        int u=read(),v=read();
        link(u,v),link(v,u);
    }
    dfs(1,0),dfs2(1);
    for(int j=1;j<=17;j++)for(int i=1;i<=n;i++)fa[i][j]=fa[fa[i][j-1]][j-1];
    while(m--){
        int u=read(),v=read();
        if(dep[u]>dep[v])swap(u,v);
        int lca=LCA(u,v);
        ll all,ans;
        if(lca==u){
            int son=jump(v,dep[v]-dep[u]-1);
            int sz1=sz[v],sz2=sz[1]-sz[son];
            all=1ll*sz1*sz2,ans=0;
            ans+=1ll*(sum[v]-dep[v]*sz1)*sz2;
            ans+=1ll*(tot[son]+sz2*dep[u])*sz1;
            ans+=1ll*all*(dep[v]-dep[u]+1);
        }
        else{
            all=1ll*sz[u]*sz[v],ans=0;
            ans+=1ll*sz[u]*(sum[v]-dep[v]*sz[v]);
            ans+=1ll*sz[v]*(sum[u]-dep[u]*sz[u]);
            ans+=1ll*all*(dep[u]+dep[v]-2*dep[lca]+1);
        }
    	//ll g=gcd(all,ans);
        //printf("%lld/%lld\n",ans/g,all/g);
    	printf("%.7f\n",1.0*ans/all);
	}
}