【BZOJ1227】[SDOI2009]虔诚的墓主人

E. 虔诚的墓主人

题目描述

小W 是一片新造公墓的管理人。公墓可以看成一块N×M 的矩形，矩形的每个格点，要么种着一棵常青树，要么是一块还没有归属的墓地。当地的居民都是非常虔诚的基督徒，他们愿意提前为自己找一块合适墓地。为了体现自己对主的真诚，他们希望自己的墓地拥有着较高的虔诚度。一块墓地的虔诚度是指以这块墓地为中心的十字架的数目。一个十字架可以看成中间是墓地，墓地的正上、正下、正左、正右都有恰好k 棵常青树。小W 希望知道他所管理的这片公墓中所有墓地的虔诚度总和是多少

输入格式

第一行包含两个用空格分隔的正整数N 和M，表示公墓的宽和长，因此这个矩形公墓共有(N+1) ×(M+1)个格点，左下角的坐标为(0, 0)，右上角的坐标为(N, M)。第二行包含一个正整数W，表示公墓中常青树的个数。第三行起共W 行，每行包含两个用空格分隔的非负整数xi和yi，表示一棵常青树的坐标。输入保证没有两棵常青树拥有相同的坐标。最后一行包含一个正整数k，意义如题目所示。

输出格式

包含一个非负整数，表示这片公墓中所有墓地的虔诚度总和。为了方便起见，答案对2,147,483,648 取模。

样例

样例输入

5 6
13
0 2
0 3
1 2
1 3
2 0
2 1
2 4
2 5
2 6
3 2
3 3
4 3
5 2
2

样例输出

6

数据范围与提示

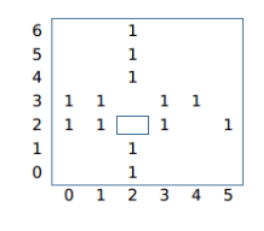
图中，以墓地(2, 2)和(2, 3)为中心的十字架各有3个，即它们的虔诚度均为3。其他墓地的虔诚度为0。 所有数据满足1 ≤ N, M ≤ 1,000,000,000，0 ≤ xi ≤ N，0 ≤ yi ≤ M，1 ≤ W ≤ 100,000， 1 ≤ k ≤ 10。存在50%的数据，满足1 ≤ k ≤ 2。存在25%的数据，满足1 ≤ W ≤ 10000。 注意：”恰好有k颗树“，这里的恰好不是有且只有，而是从>=k的树中恰好选k棵

树状数组+离散化+组合数

真的是个神仙题，主要是代码打得太乱（逢离散化必挂），颓了测试点才调出来…

M，N远大于W，铁定要离散化，然后W²其实就可以AC了（数据有点水啊），但是是可以被卡掉的，

对于一个墓地，设他的上下左右分别有u[],d[],l[],r[]颗树，则他的虔诚度=C(u,k)*C(d,k)*C(l,k)*C(r,k),

对于同一行两颗常青树a，b之间的空地，他们的l[]和r[]是一样的，所以可以考虑用树状数组维护这一行的每个点C(u,k)*C(d,k)的前缀和，

ans+=C(l[a]+1,k)*C(r[b]+1,k)*(ask(b-1)-ask(a)),换行时单点修改即可。

#include<map>
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define LL long long
#define mod 2147483648
#define ma(x) memset(x,0,sizeof(x))
using namespace std;
LL N,M,W,k;
LL C[100010][15];
LL xi[100010],yi[100010],tx[100010],ty[100010];
LL h[100010],l[100010];
LL ss[100010],xx[100010];
LL maxx,maxy;
vector<int> inc[100010];
LL Ch[100100];
int lowbit(int x){return x&(-x);}
void add(int x,LL y);
LL ask(int x);
void xget_C(int maxn);
signed main()
{
//	freopen("25.in","r",stdin);

        scanf("%lld%lld%lld",&N,&M,&W);
        for(int i=1;i<=W;i++)scanf("%d%d",&xi[i],&yi[i]),tx[i]=xi[i],ty[i]=yi[i];
	cin>>k;
	xget_C(100000);
	sort(xi+1,xi+W+1);
	maxx=unique(xi+1,xi+W+1)-xi-1;
	sort(yi+1,yi+W+1);
	maxy=unique(yi+1,yi+W+1)-yi-1;
	for(int i=1;i<=W;i++)
	{
		int t1=lower_bound(xi+1,xi+maxx+1,tx[i])-xi;
		int t2=lower_bound(yi+1,yi+maxy+1,ty[i])-yi;
		h[t2]++,l[t1]++;
		inc[t2].push_back(t1);
	}
	for(int i=1;i<=maxy;i++)
		sort(inc[i].begin(),inc[i].end());
	for(int i=1;i<=maxx;i++)ss[i]=l[i];
	LL ans=0;
	for(int i=1;i<=maxy;i++)
	{
		for(int j=0;j<inc[i].size();j++)
		{
			ss[inc[i][j]]--,xx[inc[i][j]]++;
			LL te1=(C[ss[inc[i][j]]][k]*C[xx[inc[i][j]]][k])%mod,
			   te2=(C[ss[inc[i][j]]+1][k]*C[xx[inc[i][j]]-1][k])%mod;
			add(inc[i][j],(te1-te2+mod)%mod);
		}
		if(i>k && h[i]>=2*k)
		for(int j=k;j+k<=inc[i].size();j++)
			if(j && inc[i][j]!=inc[i][j-1]+1)
				ans=(ans+C[j][k]*C[inc[i].size()-j][k]*(ask(inc[i][j]-1)-ask(inc[i][j-1])))%mod;
	}
	cout<<(ans%mod+mod)%mod<<endl;
}
void xget_C(int maxn)
{
	C[0][0]=1;
	for(int i=1;i<=maxn;i++)
	{
		C[i][0]=1;
		for(int j=1;j<=min(i,11);j++)
			C[i][j]=(C[i-1][j-1]+C[i-1][j])%mod;
	}
}
void add(int x,LL y)
{
	while(x<=maxx)
	{
		Ch[x]=(Ch[x]+y)%mod;
		x+=lowbit(x);
	}
}
LL ask(int x)
{
	LL ans=0;
	while(x)
	{
		ans=(ans+Ch[x])%mod;
		x-=lowbit(x);
	}
	return ans;
}