牛客寒假训练营2-C算概率

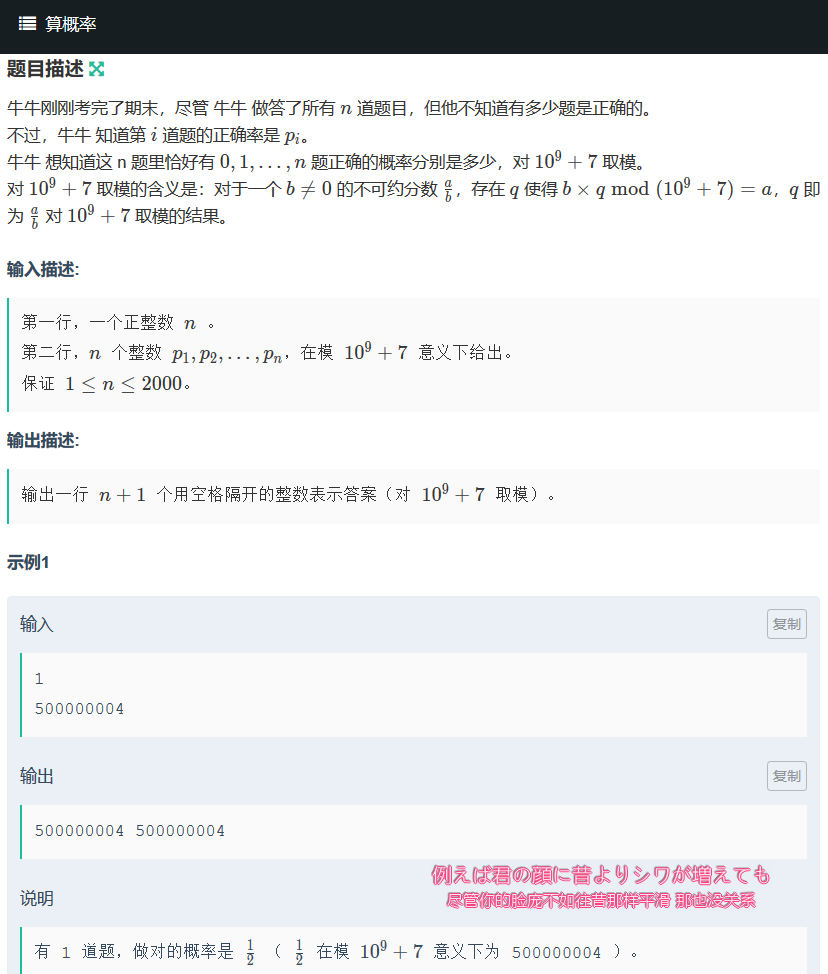
思路

　　用 f(i,j) 来表示当前做了i道题，共做对了j道题

　　状态 f[i][j] = f[i-1][j] * (1-p[i]) + f[i-1][j-1] * p[i]

　　第一种：由于i-1时对了j题，所以第i题做错了；

　　第二种：由于i-1时对了j-1题，所以第i题对了；

　　时间复杂度O（n^2)

CODE

 #include <bits/stdc++.h>
 #define dbg(x) cout << #x << "=" << x << endl
 
 using namespace std;
 typedef long long LL;
 
 template<class T>inline void read(T &res)
 {
     char c;T flag=;
     while((c=getchar())<''||c>'')if(c=='-')flag=-;res=c-'';
     while((c=getchar())>=''&&c<='')res=res*+c-'';res*=flag;
 }
 
 namespace _buff {
     const size_t BUFF =  << ;
     char ibuf[BUFF], *ib = ibuf, *ie = ibuf;
     char getc() {
         if (ib == ie) {
             ib = ibuf;
             ie = ibuf + fread(ibuf, , BUFF, stdin);
         }
         return ib == ie ? - : *ib++;
     }
 }
 
 int qread() {
     using namespace _buff;
     int ret = ;
     bool pos = true;
     char c = getc();
     for (; (c < '' || c > '') && c != '-'; c = getc()) {
         assert(~c);
     }
     if (c == '-') {
         pos = false;
         c = getc();
     }
     for (; c >= '' && c <= ''; c = getc()) {
         ret = (ret << ) + (ret << ) + (c ^ );
     }
     return pos ? ret : -ret;
 }
 
 const int kmaxn = ;
 LL f[kmaxn][kmaxn];
 const LL mod = 1e9 + ;
 int n;
 LL p[kmaxn];
 
 int main()
 {
     scanf("%d",&n);
     for(int i = ; i <= n; ++i) {
         scanf("%lld",&p[i]);
     }
     f[][] = ;
     for(int i = ; i <= n; ++i) {
         f[i][] = f[i-][] * (mod+-p[i]) % mod;
         for(int j = ; j <= n; ++j) {
             f[i][j] = ((f[i-][j]*(i-p[i]+mod)) % mod + f[i-][j-]*(mod+p[i]) % mod)% mod;
         }
     }
     for(int i = ; i < n; ++i) {
         printf("%lld ",f[n][i]);
     }
     printf("%lld\n",f[n][n]);
     return ;
 }