P2046 [NOI2010]海拔平面图转对偶图（最小割-》最短路）

$ \color{#0066ff}{ 题目描述 }$

YT市是一个规划良好的城市，城市被东西向和南北向的主干道划分为n×n个区域。简单起见，可以将YT市看作一个正方形，每一个区域也可看作一个正方形。从而，YT城市中包括(n+1)×(n+1)个交叉路口和2n×(n+1)条双向道路（简称道路），每条双向道路连接主干道上两个相邻的交叉路口。下图为一张YT市的地图(n = 2)，城市被划分为2×2个区域，包括3×3个交叉路口和12条双向道路。

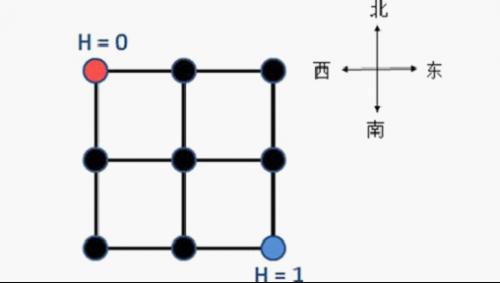
小Z作为该市的市长，他根据统计信息得到了每天上班高峰期间YT市每条道路两个方向的人流量，即在高峰期间沿着该方向通过这条道路的人数。每一个交叉路口都有不同的海拔高度值，YT市市民认为爬坡是一件非常累的事情，每向上爬h的高度，就需要消耗h的体力。如果是下坡的话，则不需要耗费体力。因此如果一段道路的终点海拔减去起点海拔的值为h(注意h可能是负数)，那么一个人经过这段路所消耗的体力是max{0, h}（这里max{a, b}表示取a, b两个值中的较大值）。

小Z还测量得到这个城市西北角的交叉路口海拔为0，东南角的交叉路口海拔为1(如上图所示)，但其它交叉路口的海拔高度都无法得知。小Z想知道在最理想的情况下（即你可以任意假设其他路口的海拔高度），每天上班高峰期间所有人爬坡消耗的总体力和的最小值。

$\color{#0066ff}{输入格式}$

第一行包含一个整数n，含义如上文所示。

接下来4n(n + 1)行，每行包含一个非负整数分别表示每一条道路每一个方向的人流量信息。输入顺序：n(n + 1)个数表示所有从西到东方向的人流量，然后n(n + 1)个数表示所有从北到南方向的人流量，n(n + 1)个数表示所有从东到西方向的人流量，最后是n(n + 1)个数表示所有从南到北方向的人流量。对于每一个方向，输入顺序按照起点由北向南，若南北方向相同时由西到东的顺序给出(参见样例输入)。

$\color{#0066ff}{输出格式}$

仅包含一个数，表示在最理想情况下每天上班高峰期间所有人爬坡所消耗的总体力和（即总体力和的最小值），结果四舍五入到整数。

$\color{#0066ff}{输入样例}$

$\color{#0066ff}{输出样例}$

$\color{#0066ff}{数据范围与提示}$

对于20%的数据：n ≤ 3；

对于50%的数据：n ≤ 15；

对于80%的数据：n ≤ 40；

对于100%的数据：1 ≤ n ≤ 500，0 ≤ 流量 ≤ 1,000,000且所有流量均为整数。

$\color{#0066ff}{题解}$

显然如果没有起点终点的高度问题，我们让所有点的海拔都是0，肯定是最优的，答案为0

但是现在限制了终点的海拔为1，显然最优情况肯定是对于一条从起点到终点的路径，找出一个中间边，使得那条边的所有人从0走到1，前半段都是0到0，后半段都是0到1

选择了那条0到1的边，那么每个人都会花费1的体力，也就是说代价是那条边（有向）的人数

所以就是个裸的最小割，然而只能拿到80分

最小割可以转化为对偶图跑最短路！就是这些点和线把平面割成了一些小平面，每个小平面是一个点，求最短路就是答案，注意方向，原图是左上到右下，对偶图是左下到右上

#include<bits/stdc++.h>

#define LL long long

LL read() {

	char ch; LL x = 0, f = 1;

	while(!isdigit(ch = getchar()))(ch == '-') && (f = -f);

	for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 1) + (x << 3) + (ch ^ 48));

	return x * f;

}

template<class T> bool chkmax(T &a, const T &b) { return a < b? a = b, 1 : 0; }

template<class T> bool chkmin(T &a, const T &b) { return b < a? a = b, 1 : 0; }

const int maxn = 3e5 + 10;

const int inf = 0x7fffffff;

struct node {

	int to, dis;

	node *nxt;

	node(int to = 0, int dis = 0, node *nxt = NULL): to(to), dis(dis), nxt(nxt) {}

};

node *head[maxn];

bool vis[maxn];

int dis[maxn], id[666][666];

int n, m, s, t;

int dij() {

	std::priority_queue<std::pair<int, int>, std::vector<std::pair<int, int> >, std::greater<std::pair<int, int> > > q;

	for(int i = s; i <= t; i++) dis[i] = inf;

	q.push(std::make_pair(dis[s] = 0, s));

	while(!q.empty()) {

		int tp = q.top().second; q.pop();

		if(vis[tp]) continue;

		vis[tp] = true;

		for(node *i = head[tp]; i; i = i->nxt)

			if(dis[i->to] > dis[tp] + i->dis)

				q.push(std::make_pair(dis[i->to] = dis[tp] + i->dis, i->to));

	}

	return dis[t];

}

void add(int from, int to, int dis) { head[from] = new node(to, dis, head[from]); }

int main() {

	m = (n = read()) + 1;

	s = 0, t = n * n + 1;

	for(int i = 1; i <= n; i++)

		for(int j = 1; j <= n; j++)

			id[i][j] = (i - 1) * n + j;

	for(int i = 1; i <= m; i++)

		for(int j = 1; j <= n; j++) {

			if(i == 1) add(id[i][j], t, read());

			else if(i == m) add(s, id[i - 1][j], read());

			else add(id[i][j], id[i - 1][j], read());

		}

	for(int i = 1; i <= n; i++)

		for(int j = 1; j <= m; j++) {

			if(j == 1) add(s, id[i][j], read());

			else if(j == m) add(id[i][j - 1], t, read());

			else add(id[i][j - 1], id[i][j], read());

		}

	for(int i = 1; i <= m; i++)

		for(int j = 1; j <= n; j++) {

			if(i == 1) add(t, id[i][j], read());

			else if(i == m) add(id[i - 1][j], s, read());

			else add(id[i - 1][j], id[i][j], read());

		}

	for(int i = 1; i <= n; i++)

		for(int j = 1; j <= m; j++) {

			if(j == 1) add(id[i][j], s, read());

			else if(j == m) add(t, id[i][j - 1], read());

			else add(id[i][j], id[i][j - 1], read());

		}

	printf("%d\n", dij());

	return 0;

}