求解范围中 gcd（a,b）== prime 的有序对数

题目：

给定整数N，求1<=x,y<=N且Gcd(x,y)为素数的
数对(x,y)有多少对.

输入：

一个整数N。

输出：

如题。

Sample  Input

4

Sample Output

4

Hint

对于样例(2,2),(2,4),(3,3),(4,2)

1<=N<=10^7

思路：

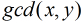
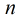
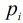
对于本题，因为是使得为质数，所以必然要枚举小于等于的质数，那么对于每一个质数，

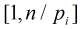
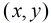
只需要求在区间中，满足有序对互质的对数。

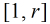
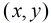
也就是说，现在问题转化为：在区间中，存在多少个有序对使得互质，这个问题就简单啦，因为

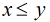
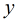
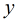
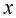
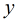
是有序对，不妨设，那么我们如果枚举每一个，小于有多少个与互素，这正是欧拉函数。所以

我们可以递推法求欧拉函数，将得到的答案乘以2即可，但是这里乘以2后还有漏计算了的，那么有哪些呢？

是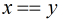且为素数的情况，再加上就行了。

另外，在bzoj上好像空间限制的原因要用埃氏筛法筛质数，而在nyzoj上，数据点较大，最好用欧拉筛筛质数。

//nyzoj（乌市一中在线评测） www.nyzoj.com:5283 题目：blcup （10053）

代码如下：

//bzoj AC版：

#include<cstdio>
typedef long long ll;
const ll N=1e7+;
ll n,f[N],phi[N];
bool prime[N];
ll p[N],cnt;
void prework()
{
    for (int i=;i<=n;i++) prime[i]=;
    for (int i=;i<=n;i++)
    {
        if (prime[i])
        {
            p[++cnt]=i;
            for (int j=i<<;j<=n;j+=i)
              prime[j]=;
        }
    }
}
void Er()
{
    for (int i=;i<=n;i++) phi[i]=i;
    for (int i=;i<=n;i+=) phi[i]>>=;
    for (int i=;i<=n;i+=)
    {
        if (phi[i]==i)
        for (int j=i;j<=n;j+=i)
          phi[j]=phi[j]-phi[j]/i;
    }
    f[]=;
    for (int i=;i<=n;i++)
      f[i]=f[i-]+(phi[i]<<);
}
ll solve()
{
    ll ans=;
    for (int i=;i<=cnt;i++)
    {
        ans+=  + f[n/p[i]] ;
    }
    return ans;
}
int main()
{
    scanf ("%lld",&n);
    prework();
    Er();
    printf("%lld",solve());
    return ;
}

//nyzoj AC 版：

#include<cstdio>
typedef long long ll;
const ll N=1e7+;
ll n,f[N],phi[N];
int v[N];
ll p[N],cnt;
void prework()
{
    for (int i=;i<=n;i++)
    {
        if (v[i]==)
        {
            v[i]=i; p[++cnt]=i;
        }
        for (int j=;j<=cnt;j++)
        {
            if (p[j]>v[i] || p[j]>n/i) break;
            v[i*p[j]]=p[j];
        }
    }
}
void Er()//递推求欧拉函数
{
    for (int i=;i<=(n>>);i++) phi[i]=i;
    for (int i=;i<=(n>>);i+=) phi[i]>>=;
    for (int i=;i<=(n>>);i+=)
    {
        if (phi[i]==i)
        for (int j=i;j<=(n>>);j+=i)
          phi[j]=phi[j]-phi[j]/i;
    }
    f[]=;
    for (int i=;i<=(n>>);i++)
      f[i]=f[i-]+(phi[i]<<);
}
ll solve()
{
    ll ans=;
    for (int i=;i<=cnt;i++)
    {
        ans+=  + f[n/p[i]] ;
    }
    return ans;
}
int main()
{
    scanf ("%lld",&n);
    prework();
    Er();
    printf("%lld",solve());
    return ;
}