【转载】 强化学习（五）用时序差分法（TD）求解

原文地址：

https://www.cnblogs.com/pinard/p/9529828.html

--------------------------------------------------------------------------------------------------

在强化学习（四）用蒙特卡罗法（MC）求解中，我们讲到了使用蒙特卡罗法来求解强化学习问题的方法，虽然蒙特卡罗法很灵活，不需要环境的状态转化概率模型，但是它需要所有的采样序列都是经历完整的状态序列。如果我们没有完整的状态序列，那么就无法使用蒙特卡罗法求解了。本文我们就来讨论可以不使用完整状态序列求解强化学习问题的方法：时序差分(Temporal-Difference, TD)。

　　　　时序差分这一篇对应Sutton书的第六章部分和UCL强化学习课程的第四讲部分，第五讲部分。

1. 时序差分TD简介

时序差分法和蒙特卡罗法类似，都是不基于模型的强化学习问题求解方法。所以在上一篇定义的不基于模型的强化学习控制问题和预测问题的定义，在这里仍然适用。

回顾蒙特卡罗法中计算状态收获的方法是：

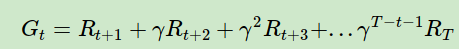
而对于时序差分法来说，我们没有完整的状态序列，只有部分的状态序列，那么如何可以近似求出某个状态的收获呢？回顾强化学习（二）马尔科夫决策过程(MDP)中的贝尔曼方程：

2. 时序差分TD的预测问题求解

　　　　这里我们用一个简单的例子来看看蒙特卡罗法和时序差分法求解预测问题的不同。

　　　　假设我们的强化学习问题有A,B两个状态，模型未知，不涉及策略和行为。只涉及状态转化和即时奖励。一共有8个完整的状态序列如下：

　　　　① A,0,B,0 ②B,1 ③B,1 ④ B,1 ⑤ B,1 ⑥B,1 ⑦B,1 ⑧B,0

首先我们按蒙特卡罗法来求解预测问题。由于只有第一个序列中包含状态A，因此A的价值仅能通过第一个序列来计算，也就等同于计算该序列中状态A的收获：

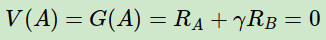
　　　　对于B，则需要对其在8个序列中的收获值来平均，其结果是6/8。

再来看看时序差分法求解的过程。其收获是在计算状态序列中某状态价值时是应用其后续状态的预估价值来计算的，对于B来说，它总是终止状态，没有后续状态，因此它的价值直接用其在8个序列中的收获值来平均，其结果是6/8。

对于A，只在第一个序列出现，它的价值为：

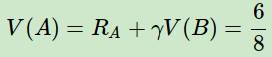
从上面的例子我们也可以看到蒙特卡罗法和时序差分法求解预测问题的区别。

• 一是时序差分法在知道结果之前就可以学习，也可以在没有结果时学习，还可以在持续进行的环境中学习，而蒙特卡罗法则要等到最后结果才能学习，时序差分法可以更快速灵活的更新状态的价值估计，这在某些情况下有着非常重要的实际意义。

• 二是时序差分法在更新状态价值时使用的是TD 目标值，即基于即时奖励和下一状态的预估价值来替代当前状态在状态序列结束时可能得到的收获，是当前状态价值的有偏估计，而蒙特卡罗法则使用实际的收获来更新状态价值，是某一策略下状态价值的无偏估计，这一点蒙特卡罗法占优。

• 三是虽然时序差分法得到的价值是有偏估计，但是其方差却比蒙特卡罗法得到的方差要低，且对初始值敏感，通常比蒙特卡罗法更加高效。

从上面的描述可以看出时序差分法的优势比较大，因此现在主流的强化学习求解方法都是基于时序差分的。后面的文章也会主要基于时序差分法来扩展讨论。

3. n步时序差分

　　　　当n越来越大，趋于无穷，或者说趋于使用完整的状态序列时，n步时序差分就等价于蒙特卡罗法了。

对于n步时序差分来说，和普通的时序差分的区别就在于收获的计算方式的差异。那么既然有这个n步的说法，那么n到底是多少步好呢？如何衡量n的好坏呢？我们在下一节讨论。

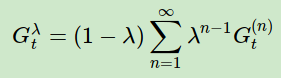
如果给每一个状态引入一个数值：效用(eligibility, E) 来表示该状态对后续状态的影响，就可以同时利用到上述两个启发。而所有状态的效用值总称为效用迹(eligibility traces,ES)。定义为：

也许有人会问，这前向的式子和反向的式子看起来不同啊，是不是不同的逻辑呢？其实两者是等价的。现在我们从前向推导一下反向的更新式子。

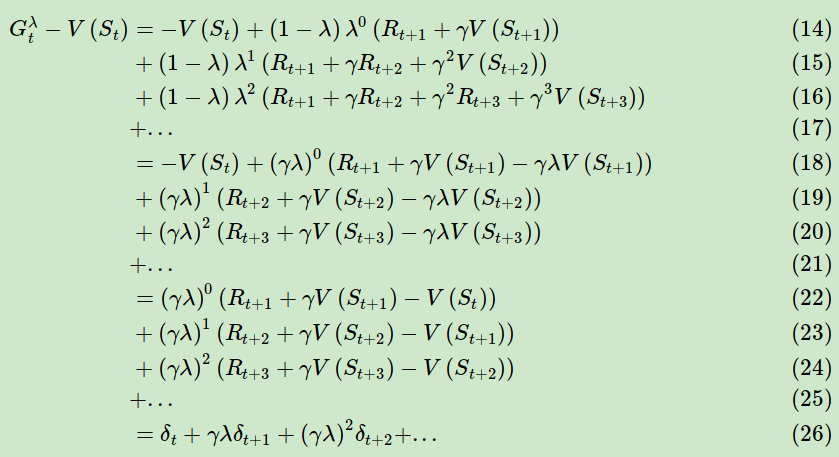
可以看出前向TD误差和反向的TD误差实际上一致的。

5.  时序差分的控制问题求解

6. 时序差分小结

时序差分和蒙特卡罗法比它更加灵活，学习能力更强，因此是目前主流的强化学习求解问题的方法，现在绝大部分强化学习乃至深度强化学习的求解都是以时序差分的思想为基础的。因此后面我们会重点讨论。

　　　　下一篇我们会讨论时序差分的在线控制算法SARSA。

（欢迎转载，转载请注明出处。欢迎沟通交流： liujianping-ok@163.com）

--------------------------------------------------------------------------------------------------------

TD(λ)