KMP算法关键

Knuth-Morris-Pratt Algorithm

当初写这个博客之后一年多，再次看发现当初并不是完全弄明白了。这里为了“避免重复制造轮子”，引用大神博客。

http://blog.csdn.net/v_july_v/article/details/7041827

特殊的 next[ ] 数组

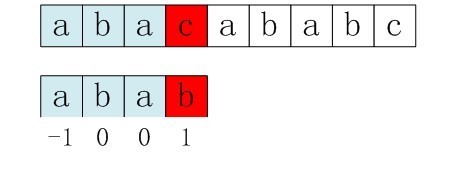
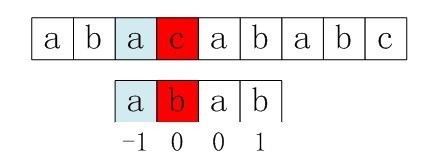
next数组相当于“最大长度值”(前缀后缀的最大公共元素长度) 整体向右移动一位，然后初始值赋为-1

求next数组

	//优化过后的next 数组求法
	void GetNextval(char* p, int next[])
	{
	    int pLen = strlen(p);
	    next[0] = -1;
	    int k = -1;
	    int j = 0;
	    while (j < pLen - 1)
	    {
	        //p[k]表示前缀，p[j]表示后缀
	        if (k == -1 || p[j] == p[k])
	        {
	            ++j;
	            ++k;
	            if (p[j] != p[k])
	                next[j] = k;   //之前只有这一行
	            else
	      //因为不能出现p[j] = p[ next[j ]]，所以当出现时需要继续递归，k = next[k] = next[next[k]]
	                next[j] = next[k];
	        }
	        else
	        {
	            k = next[k];
	        }
	    }
	}

 

 

注意：有了上面的这段代码效率更高

if (p[j] != p[k])
	next[j] = k;   //之前只有这一行
else
	//因为不能出现p[j] = p[ next[j ]]，所以当出现时需要继续递归，k = next[k] = next[next[k]]
	next[j] = next[k];

具体原理如下：

当两个字符串为下面所示的情况：

右移位后，b又跟c失配。事实上，因为在上一步的匹配中，已经得知p[3]
= b，与s[3] = c失配，而右移两位之后，让p[ next[3] ] =p[1] = b再跟s[3]匹配时，必然失配。问题出在哪呢？

匹配函数

 

	int KmpSearch(char* s, char* p)
	{
	    int i = 0;
	    int j = 0;
	    int sLen = strlen(s);
	    int pLen = strlen(p);
	    while (i < sLen && j < pLen)
	    {
	        //①如果j = -1，或者当前字符匹配成功（即S[i] == P[j]），都令i++，j++
	        if (j == -1 || s[i] == p[j])
	        {
	            i++;
	            j++;
	        }
	        else
	        {
	            //②如果j != -1，且当前字符匹配失败（即S[i] != P[j]），则令 i 不变，j = next[j]
	            //next[j]即为j所对应的next值
	            j = next[j];
	        }
	    }
	    if (j == pLen)
	        return i - j;
	    else
	        return -1;
	}