Verilog 加法器和减法器(1)

两个一位的二进制数x,y相加，假设和为s，进位为cout，其真值表为：

从真值表中，我们可以得到：s = x^y, cout = x&y，实现两个一位数相加的逻辑电路称为半加器。

实现该电路的verilog代码如下：

module halfadd(x,y,s,cout);

  input x;
  input y;

  output s;
  output cout;

  assign s = x^y;
  assign cout = x&y;

endmodule

相对应的testbench文件如下代码。在代码中，我们采用系统函数$random来产生随机激励。半加器电路中并没有使用时钟，但在testbench中，产生了时钟信号，主要是为了功能验证时候，有一个时间单位信号，便于检查结果。

`timescale 1ns/1ns
`define clock_period 20

module halfadd_tb;
  reg  x,y;

  wire cout;
  wire s;
  reg clk;

  halfadd halfadd_0(
						.x(x),
						.y(y),
						.s(s),
						.cout(cout)
                  );

  initial clk = 0;
  always #(`clock_period/2) clk = ~clk;

  initial begin
     x = 0;
     repeat(20)
	    #(`clock_period) x = $random;

  end

  initial begin
     y = 0;
     repeat(20)
	    #(`clock_period) y = $random;

  end

  initial begin
     #(`clock_period*20)
	  $stop;
  end

endmodule

在quartus II中，分析与综合后，用rtl view 可以得到 halfadd的电路如下，和我们预想的一样。

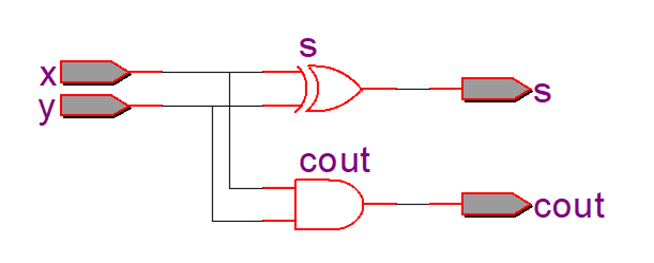
功能仿真结果如下，从波形中可以看到结果正确。

全编译后，在Cyclone IV E-EP4CE10F17C8中的门级仿真结果如下，输入和输出之间，会有几ns的时延。

通常，我们更感兴趣的是多位二进制数的相加，在多位二进制数相加时，对每一位而言，除了考虑相加的两位数(第i位)，还要考虑来自低位(i-1位)的进位。实现带低位进位的两个一位数相加的逻辑电路，称为全加器。

它的真值表如下：

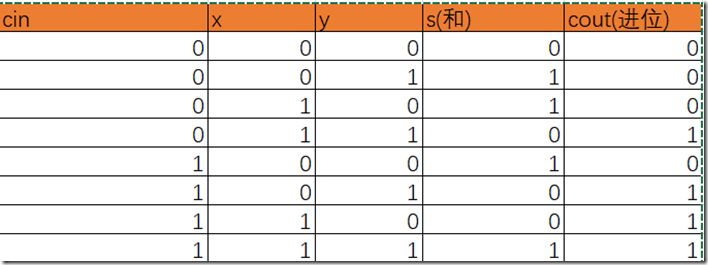
从真值表中，我们可以得知：s = ~x & y & ~cin + x&~y&~cin+~x&~y&cin+x&y&cin = (~x&y+x&~y)&~cin+(~x&~y+x&y)&cin=(x^y)&~cin+~(x^y)&cin=x^y^cin，

这儿我们用~表示非，+表示或。cout = x&y+x&cin+y&cin

全加器verilog代码如下：

module fulladd(cin,x,y,s,cout);

  input cin;
  input x;
  input y;

  output s;
  output cout;

  assign s = x^y^cin;
  assign cout = (x&y)|(x&cin)|(y&cin);

endmodule

对应的testbench代码如下：

`timescale 1ns/1ns
`define clock_period 20

module fulladd_tb;
  reg  cin,x,y;

  wire cout;
  wire s;
  reg clk;

  fulladd fulladd_0(
                  .cin(cin),
						.x(x),
						.y(y),
						.s(s),
						.cout(cout)
                  );

  initial clk = 0;
  always #(`clock_period/2) clk = ~clk;

  initial begin
     x = 0;
     repeat(20)
	    #(`clock_period) x = $random;

  end

  initial begin
     y = 0;
     repeat(20)
	    #(`clock_period) y = $random;

  end

  initial begin
     cin = 0;
     repeat(2)
	    #(`clock_period*10) cin = {$random};

  end

  initial begin
     #(`clock_period*20)
	  $stop;
  end

endmodule

从rtl view中，可以看到全加器逻辑电路图如下：包括3个与门，一个三输入的异或门，一个三输入的或门。

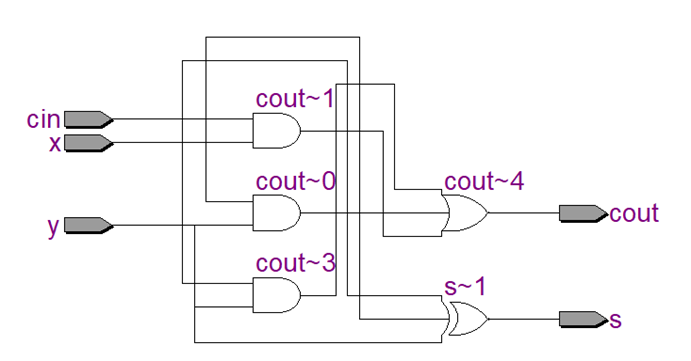
功能仿真和门级仿真的波形如下，信号符合预期。