混沌分形之迭代函数系统(IFS)
IFS是分形的重要分支。它是分形图像处理中最富生命力而且最具有广阔应用前景的领域之一。这一工作最早可以追溯到Hutchinson于1981年对自相似集的研究。美国科学家M.F.Barnsley于1985年发展了这一分形构型系统,并命名为迭代函数系统(Iterated Function System,IFS),后来又由Stephen Demko等人将其公式化,并引入到图像合成领域中。IFS将待生成的图像看做是由许多与整体相似的(自相似)或经过一定变换与整体相似的(自仿射)小块拼贴而成。
算法:
1.设定一个起始点(x0,y0)及总的迭代步数。
2.以概率P选取仿射变换W,形式为
X1=a*x0 + b*y0 + e
Y1=c*x0 + d*y0 + f
或
X1=(a * x0*cosf(c/180)) - (b * y0*sinf(d/180)) + e
Y1=(a * x0*sinf(c/180)) + (b * y0*cosf(d/180)) + f
3.以W作用点(x0,y0),得到新坐标(x1,y1)。
4.令x0=x1,y0=y1。
5.在屏幕上打出(x0,y0)。
6.重返第2步,进行下一次迭代,直到迭代次数大于总步数为止。
(1)三角形
class IFSTriangle : public FractalEquation
{
public:
IFSTriangle()
{
m_StartX = 0.0f;
m_StartY = 0.0f;
m_StartZ = 0.0f; m_ParamA = 0.0f;
m_ParamB = 0.5f; //'IFS码赋值
m[][] = 0.5f; m[][] = ; m[][] = ; m[][] = 0.5f; m[][] = ; m[][] = ; m[][] = 0.333f;
m[][] = 0.5f; m[][] = ; m[][] = ; m[][] = 0.5f; m[][] = 0.5f; m[][] = ; m[][] = 0.333f;
m[][] = 0.5f; m[][] = ; m[][] = ; m[][] = 0.5f; m[][] = 0.25f; m[][] = 0.5f; m[][] = 0.334f;
} void IterateValue(float x, float y, float z, float& outX, float& outY, float& outZ) const
{
float a, b, c, d, e, f; //'仿射变幻中的系数 float R = (float)rand()/RAND_MAX; if (R <= m[][])
{
a = m[][]; b = m[][]; c = m[][]; d = m[][]; e = m[][]; f = m[][];
}
else if (R <= m[][] + m[][])
{
a = m[][]; b = m[][]; c = m[][]; d = m[][]; e = m[][]; f = m[][];
}
else
{
a = m[][]; b = m[][]; c = m[][]; d = m[][]; e = m[][]; f = m[][];
} outX = (a * x) + (b * y) + e*FRACTAL_RADIUS;
outY = (c * x) + (d * y) + f*FRACTAL_RADIUS;
outZ = z;
} bool IsValidParamA() const {return true;}
bool IsValidParamB() const {return true;} void SetParamA(float v)
{
m_ParamA = v;
m[][] = v;
} void SetParamB(float v)
{
m_ParamB = v;
m[][] = v;
m[][] = v;
} private:
float m[][]; // '存放IFS码
};
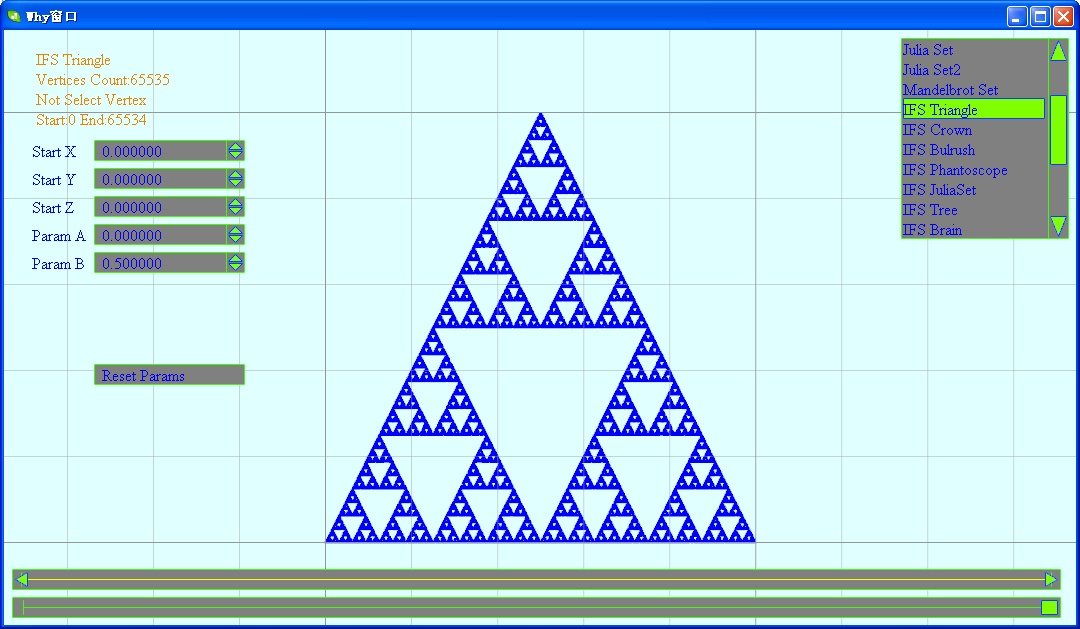
这里生成的是谢尔宾斯基三角形,但可以通过参数设置对其变形


(2)皇冠
class IFSCrown : public FractalEquation
{
public:
IFSCrown()
{
m_StartX = 0.0f;
m_StartY = 0.0f;
m_StartZ = 0.0f; m_ParamA = 2.0f; //'IFS码赋值
m[][] = 0.5f; m[][] = 0.5f; m[][] = ; m[][] = ; m[][] = ; m[][] = ; m[][] = 0.2f;
m[][] = 0.5f; m[][] = 0.5f; m[][] = ; m[][] = ; m[][] = 0.5f; m[][] = ; m[][] = 0.2f;
m[][] = 0.25f; m[][] = 0.25f; m[][] = ; m[][] = ; m[][] = 2.0f; m[][] = 2.0f;m[][] = 0.3f;
m[][] = 0.25f; m[][] = 0.25f; m[][] = ; m[][] = ; m[][] = -1.0f;m[][] = 2.0f;m[][] = 0.3f;
} void IterateValue(float x, float y, float z, float& outX, float& outY, float& outZ) const
{
float a, b, c, d, e, f; //'仿射变幻中的系数 float R = (float)rand()/RAND_MAX; if (R <= m[][])
{
a = m[][]; b = m[][]; c = m[][]; d = m[][]; e = m[][]; f = m[][];
}
else if (R <= m[][] + m[][])
{
a = m[][]; b = m[][]; c = m[][]; d = m[][]; e = m[][]; f = m[][];
}
else if (R <= m[][] + m[][] + m[][])
{
a = m[][]; b = m[][]; c = m[][]; d = m[][]; e = m[][]; f = m[][];
}
else
{
a = m[][]; b = m[][]; c = m[][]; d = m[][]; e = m[][]; f = m[][];
} outX = (a * x*cosf(c/)) - (b * y*sinf(d/)) + e*FRACTAL_RADIUS;
outY = (a * x*sinf(c/)) + (b * y*cosf(d/)) + f*FRACTAL_RADIUS;
outZ = z;
} bool IsValidParamA() const {return true;} void SetParamA(float v)
{
m_ParamA = v;
m[][] = v;
m[][] = v;
m[][] = - v;
m[][] = v;
} private:
float m[][]; // '存放IFS码
};

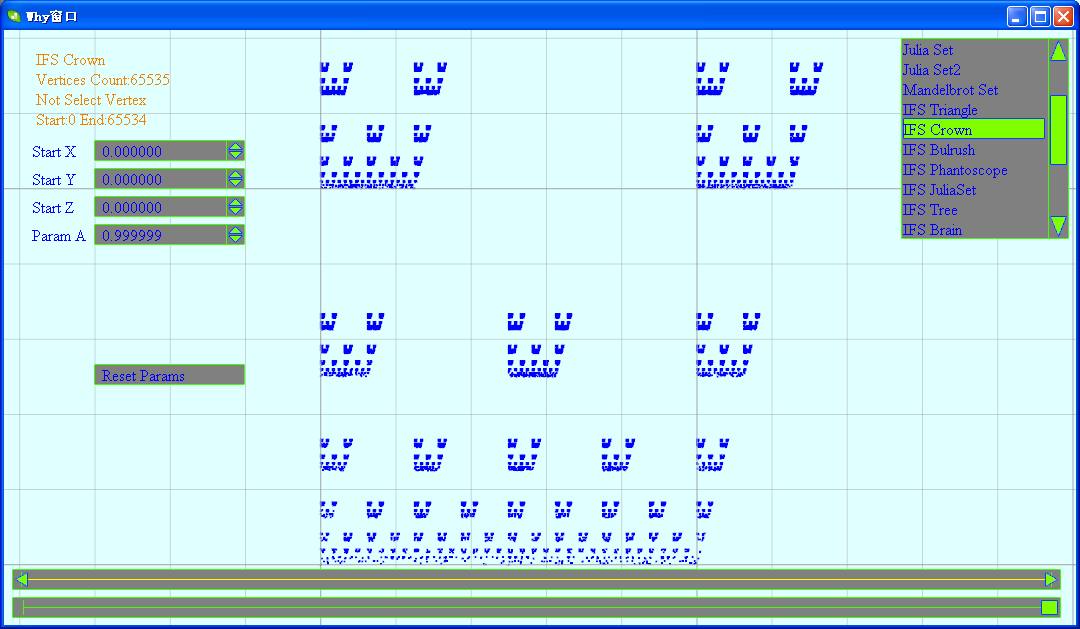
(3)芦苇
// 芦苇
class IFSBulrush : public FractalEquation
{
public:
IFSBulrush()
{
m_StartX = 0.0f;
m_StartY = 0.0f;
m_StartZ = 0.0f; m_ParamA = 10.0f; float k = m_ParamA*100.0f; //'IFS码赋值
m[][] = 0.5f; m[][] = 0.5f; m[][] = ; m[][] = ; m[][] = ; m[][] = ; m[][] = 0.3f;
m[][] = 0.5f; m[][] = 0.5f; m[][] = k; m[][] = k; m[][] = ; m[][] = k/; m[][] = 0.3f;
m[][] = 0.5f; m[][] = 0.5f; m[][] = ; m[][] = ; m[][] = 0.5f; m[][] = ; m[][] = 0.4f;
} void IterateValue(float x, float y, float z, float& outX, float& outY, float& outZ) const
{
float a, b, c, d, e, f; //'仿射变幻中的系数 float R = (float)rand()/RAND_MAX; if (R <= m[][])
{
a = m[][]; b = m[][]; c = m[][]; d = m[][]; e = m[][]; f = m[][];
}
else if (R <= m[][] + m[][])
{
a = m[][]; b = m[][]; c = m[][]; d = m[][]; e = m[][]; f = m[][];
}
else
{
a = m[][]; b = m[][]; c = m[][]; d = m[][]; e = m[][]; f = m[][];
} outX = (a * x*cosf(c/)) - (b * y*sinf(d/)) + e*FRACTAL_RADIUS;
outY = (a * x*sinf(c/)) + (b * y*cosf(d/)) + f*FRACTAL_RADIUS;
outZ = z;
} bool IsValidParamA() const {return true;} void SetParamA(float v)
{
m_ParamA = v;
float k = m_ParamA*100.0f;
m[][] = k;
m[][] = k;
m[][] = k/;
} private:
float m[][]; // '存放IFS码
};

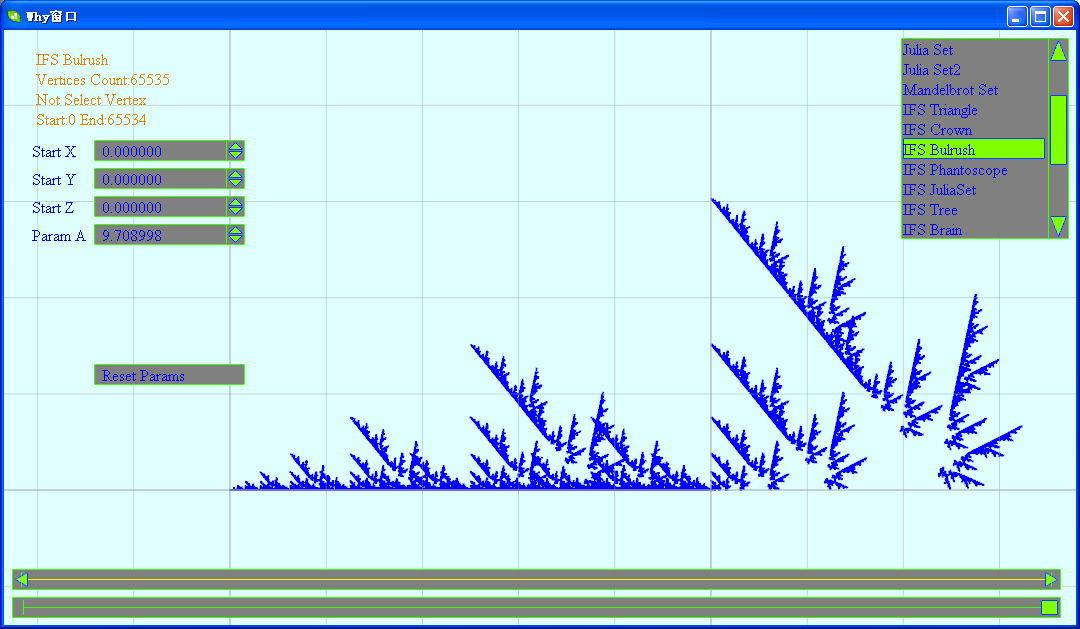

(4)万花筒
// 万花筒
class IFSPhantoscope : public FractalEquation
{
public:
IFSPhantoscope()
{
m_StartX = 0.0f;
m_StartY = 0.0f;
m_StartZ = 0.0f; m_ParamA = 2.0f; float k = m_ParamA*100.0f; //'IFS码赋值
m[][] = 0.2f; m[][] = 0.2f; m[][] = ; m[][] = ; m[][] = 0.7f; m[][] = ; m[][] = 0.2f;
m[][] = 0.2f; m[][] = 0.2f; m[][] = ; m[][] = ; m[][] =-0.7f; m[][] = ; m[][] = 0.2f;
m[][] = 0.2f; m[][] = 0.2f; m[][] = ; m[][] = ; m[][] = ; m[][] = 0.7f; m[][] = 0.2f;
m[][] = 0.2f; m[][] = 0.2f; m[][] = ; m[][] = ; m[][] = ; m[][] = -0.7f; m[][] = 0.2f;
m[][] = 0.85f; m[][] = 0.85f; m[][] = k; m[][] = k; m[][] = ; m[][] = ; m[][] = 0.2f;
} void IterateValue(float x, float y, float z, float& outX, float& outY, float& outZ) const
{
float a, b, c, d, e, f; //'仿射变幻中的系数 float R = (float)rand()/RAND_MAX; if (R <= m[][])
{
a = m[][]; b = m[][]; c = m[][]; d = m[][]; e = m[][]; f = m[][];
}
else if (R <= m[][] + m[][])
{
a = m[][]; b = m[][]; c = m[][]; d = m[][]; e = m[][]; f = m[][];
}
else if (R <= m[][] + m[][] + m[][])
{
a = m[][]; b = m[][]; c = m[][]; d = m[][]; e = m[][]; f = m[][];
}
else if (R <= m[][] + m[][] + m[][] + m[][])
{
a = m[][]; b = m[][]; c = m[][]; d = m[][]; e = m[][]; f = m[][];
}
else
{
a = m[][]; b = m[][]; c = m[][]; d = m[][]; e = m[][]; f = m[][];
} outX = (a * x*cosf(c/)) - (b * y*sinf(d/)) + e*FRACTAL_RADIUS;
outY = (a * x*sinf(c/)) + (b * y*cosf(d/)) + f*FRACTAL_RADIUS;
outZ = z;
} bool IsValidParamA() const {return true;} void SetParamA(float v)
{
m_ParamA = v;
float k = m_ParamA*100.0f;
m[][] = k;
m[][] = k;
} private:
float m[][]; // '存放IFS码
};


(5)Tree
class IFSTree : public FractalEquation
{
public:
IFSTree()
{
m_StartX = 0.0f;
m_StartY = 0.0f;
m_StartZ = 0.0f; //'IFS码赋值
m[][] = 0.195f; m[][] =-0.488f; m[][] = 0.344f; m[][] = 0.433f; m[][] = 0.4431f; m[][] = 0.2452f; m[][] = 0.25f;
m[][] = 0.462f; m[][] = 0.414f; m[][] =-0.252f; m[][] = 0.361f; m[][] = 0.2511f; m[][] = 0.5692f; m[][] = 0.25f;
m[][] =-0.058f; m[][] =-0.07f; m[][] = 0.453f; m[][] =-0.111f; m[][] = 0.5976f; m[][] = 0.0969f; m[][] = 0.25f;
m[][] =-0.035f; m[][] = 0.07f; m[][] =-0.469f; m[][] =-0.022f; m[][] = 0.4884f; m[][] = 0.5069f; m[][] = 0.2f;
m[][] =-0.637f; m[][] = 0.0f; m[][] = 0.0f; m[][] = 0.501f; m[][] = 0.8562f; m[][] = 0.2513f; m[][] = 0.05f;
} void IterateValue(float x, float y, float z, float& outX, float& outY, float& outZ) const
{
float a, b, c, d, e, f; //'仿射变幻中的系数 float R = (float)rand()/RAND_MAX; if (R <= m[][])
{
a = m[][]; b = m[][]; c = m[][]; d = m[][]; e = m[][]; f = m[][];
}
else if (R <= m[][] + m[][])
{
a = m[][]; b = m[][]; c = m[][]; d = m[][]; e = m[][]; f = m[][];
}
else if (R <= m[][] + m[][] + m[][])
{
a = m[][]; b = m[][]; c = m[][]; d = m[][]; e = m[][]; f = m[][];
}
else if (R <= m[][] + m[][] + m[][] + m[][])
{
a = m[][]; b = m[][]; c = m[][]; d = m[][]; e = m[][]; f = m[][];
}
else
{
a = m[][]; b = m[][]; c = m[][]; d = m[][]; e = m[][]; f = m[][];
} outX = a*x + b*y + e;
outY = c*x + d*y + f;
outZ = z;
} private:
float m[][]; // '存放IFS码
};
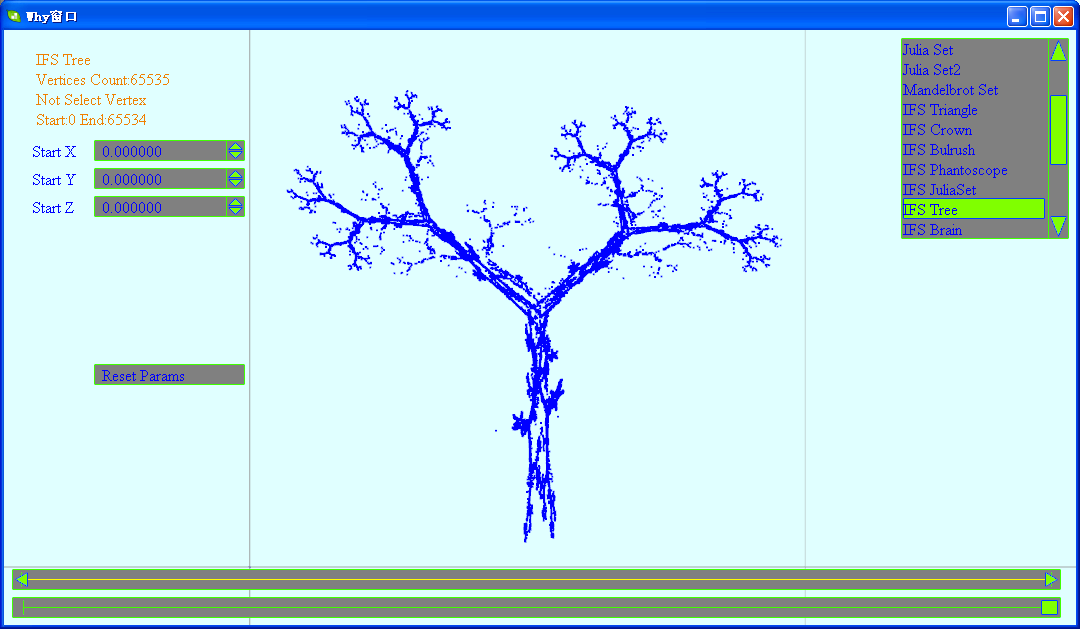
这个图形我很喜欢,所以还专门将其生成图像:

(6)大脑
class IFSBrain : public FractalEquation
{
public:
IFSBrain()
{
m_StartX = 0.0f;
m_StartY = 0.0f;
m_StartZ = 0.0f; //'IFS码赋值
//0.03 0 0 0.45 0 0 0.05;
//-0.03 0 0 -0.45 0 0.4 0.15;
//0.56 -0.56 0.56 0.56 0 0.4 0.4;
//0.56 0.56 -0.56 0.56 0 0.4 0.4;
m[][] = 0.03f; m[][] = 0.0f; m[][] = 0.0f; m[][] = 0.45f; m[][] = 0.0f; m[][] = 0.0f; m[][] = 0.05f;
m[][] =-0.03f; m[][] = 0.0f; m[][] = 0.0f; m[][] =-0.45f; m[][] = 0.0f; m[][] = 0.4f; m[][] = 0.15f;
m[][] = 0.56f; m[][] =-0.56f; m[][] = 0.56f; m[][] = 0.56f; m[][] = 0.0f; m[][] = 0.4f; m[][] = 0.4f;
m[][] = 0.56f; m[][] = 0.56f; m[][] =-0.56f; m[][] = 0.56f; m[][] = 0.0f; m[][] = 0.4f; m[][] = 0.4f;
} void IterateValue(float x, float y, float z, float& outX, float& outY, float& outZ) const
{
float a, b, c, d, e, f; //'仿射变幻中的系数 float R = (float)rand()/RAND_MAX; if (R <= m[][])
{
a = m[][]; b = m[][]; c = m[][]; d = m[][]; e = m[][]; f = m[][];
}
else if (R <= m[][] + m[][])
{
a = m[][]; b = m[][]; c = m[][]; d = m[][]; e = m[][]; f = m[][];
}
else if (R <= m[][] + m[][] + m[][])
{
a = m[][]; b = m[][]; c = m[][]; d = m[][]; e = m[][]; f = m[][];
}
else
{
a = m[][]; b = m[][]; c = m[][]; d = m[][]; e = m[][]; f = m[][];
} outX = a*x + b*y + e;
outY = c*x + d*y + f;
outZ = z;
} private:
float m[][]; // '存放IFS码
};
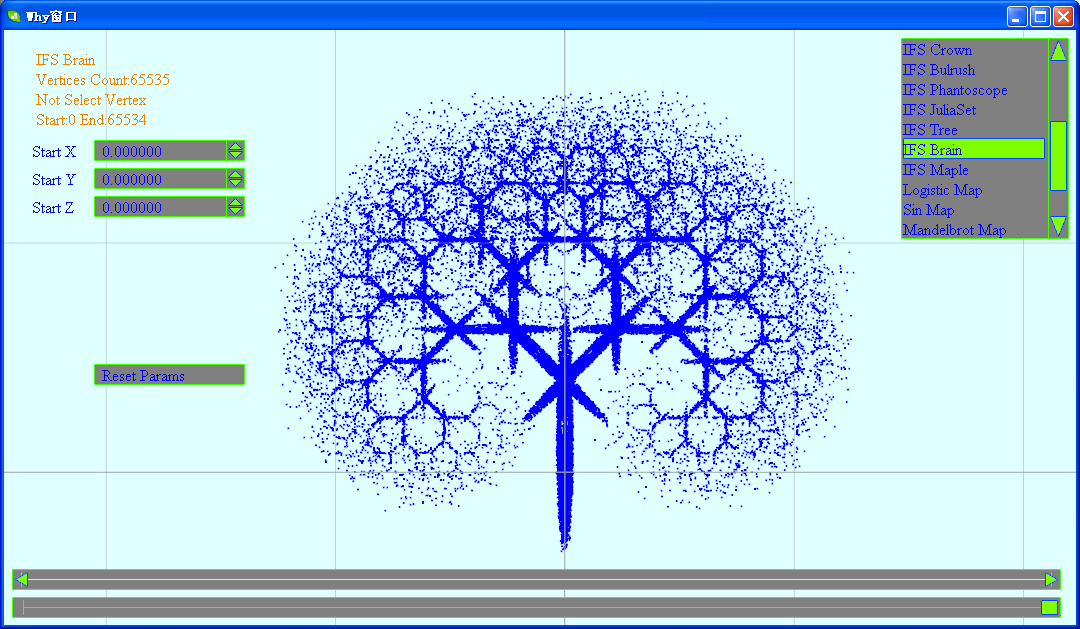
------------------------------------
关于基类FractalEquation的定义及相关软件见:混沌与分形
混沌分形之迭代函数系统(IFS)的更多相关文章
- JavaScript图形实例:迭代函数系统生成图形
迭代函数系统(Iterated Function System,IFS)可以用来创建分形图案,它是分形理论的重要分支,也是分形图形处理中最富生命力而且最具有广阔应用前景的领域之一.这一工作最早可以追溯 ...
- 混沌分形之逻辑斯蒂(Logistic)映射系统
前几天,有个同事看到我生成的一幅逻辑斯蒂分岔图像后,问我:“这是咪咪吗?”我回答:“淫者见淫.”好吧,这里将生成几种分岔映射图形,包括逻辑斯蒂映射系统,正弦映射系统和曼德勃罗映射系统.实际上这几种图形 ...
- javascript学习笔记--迭代函数
概要 这里的迭代函数指的是对数组对象的操作方法,js数组共有五个迭代函数:every.fifter.forEach.map.some. 1.every every方法,返回值为Boolean类型,tr ...
- Haskell 笔记(四)函数系统
函数系统 函数式编程当然少不了函数系统啦,在教程最初的时候就有一个最简单的函数,函数系统贯穿在Haskell全部,Haskell的函数有几个重要的性质. 首先声明一下函数的参数和返回值类型 然后有一个 ...
- Mathematica 迭代函数
学习Mathematica迭代函数的几个画图例子: 1.三角形沿着某一点旋转 verticse = {{0, 0}, {1, 0}, {1/2, Sqrt[3]/2}}; tri = Line[ver ...
- JavaScript的迭代函数与迭代函数的实现
前言 如果对技术很自信,请直接看 实现的源码 如果想回顾一下基础,请按文章顺序阅读 说到迭代方法,最先想到的是什么?forEach还是map,迭代的方法ES5提供了5种方法 以下定义来自 Ja ...
- BMDP为常规的统计分析提供了大量的完备的函数系统,如:方差分析(ANOVA)、回归分析(Regression)、非参数分析(Nonparametric Analysis)、时间序列(Times Series)等等。此外,BMDP特别擅于进行出色的生存分析(Survival Analysis )。许多年来,一大批世界范围内顶级的统计学家都曾今参与过BMDP的开发工作。这不仅使得BMDP的权威性得到
BMDP是Bio Medical Data Processing的缩写,是世界级的统计工具软件,至今已经有40多年的历史.目前在国际上与SAS.SPSS被并称为三大统计软件包.BMDP是一个大 ...
- 混沌分形之马丁(Martin)迭代
我不记得从什么地方看到的这种分形图形生成方式,再到网上找竟然一时没查到任何相关资料.没关系,总之这种图形也很漂亮多变,并且其算法比较简单.只是我最后生成的图像有点瘆人,密集恐惧症患者慎入. 相关代码如 ...
- 文件处理,三元操作符,seek()函数,迭代函数和列表解析,reduce函数
1.文件读取方类型 r,r+,w,x,a, r,读文件 w,写文件,文件内容全部删除,并将新内容从第一行开始赋值 x,写文件,只有文件不存在,可写,文件存在,报错 a,在文件莫问追加信息 r+,w+, ...
随机推荐
- 002.KVM环境部署
一 环境准备 1.1 查看是否支持虚拟化 [root@kvm-host ~]# grep -E 'vmx|svm' /proc/cpuinfo 注意:intel为vmx,amd为svm. 1.2 确定 ...
- 002.NFS相关配置项
一 配置文件(/etc/exports) 1.1 配置文件格式 <输出目录> [客户端1 选项(访问权限,用户映射,其他)] [客户端2 选项(访问权限,用户映射,其他)] 二 输出目录 ...
- error 1044 (42000):access denied for user ''@'localhost' to database 'quickapp' 解决方法
在虚拟机上重新创建一个数据库时,一直出现这个报错:error 1044 (42000):access denied for user ''@'localhost' to database 'quick ...
- Postman高级应用——串行传参和动态传参详解
Postman是一款功能强大的网页调试与发送网页HTTP请求的Chrome插件 用Postman做接口测试的时候,要把多条用例一起执行,就需要把用例连接起来,一次性执行 目录 串行传参 动态传参 使用 ...
- HTML5开启浏览器桌面通知 Web Notification
说明: 1.Chrome要求必须https才可以开启浏览器通知 2.显示图片在本服务器,不支持跨越 3.自定义声音Chrome不播放,Firefox正常播放 代码如下: <!-- /** * @ ...
- android 四大组件
韩梦飞沙 韩亚飞 313134555@qq.com yue31313 han_meng_fei_sha 活动,服务,广播接受者,内容提供者. 活动 能够提供 用户界面.服务 没有用户界面.广 ...
- WordPress 建站教程:新手搭建 WordPress个人博客图文教程(完全版)
前言 WordPress 作为动态博客的代表,至今已经有十几年历史,而且一直在更新发展中,功能强大,插件和主题丰富,WordPress搭建使用也很方便.作为个人站长和博主,很多都是从 WordPres ...
- BZOJ.1901.Dynamic Rankings(树状数组套主席树(动态主席树))
题目链接 BZOJ 洛谷 区间第k小,我们可以想到主席树.然而这是静态的,怎么支持修改? 静态的主席树是利用前缀和+差分来求解的,那么对于每个位置上的每棵树看做一个点,拿树状数组更新. 还是树状数组的 ...
- 【BZOJ-4016】最短路径树问题 Dijkstra + 点分治
4016: [FJOI2014]最短路径树问题 Time Limit: 5 Sec Memory Limit: 512 MBSubmit: 1092 Solved: 383[Submit][Sta ...
- 吴恩达-coursera-机器学习-week9
十五.异常检测(Anomaly Detection) 15.1 问题的动机 15.2 高斯分布 15.3 算法 15.4 开发和评价一个异常检测系统 15.5 异常检测与监督学习对比 15.6 选择特 ...
