sklearn调用SVM算法
1、支撑向量机SVM是一种非常重要和广泛的机器学习算法,它的算法出发点是尽可能找到最优的决策边界,使得模型的泛化能力尽可能地好,因此SVM对未来数据的预测也是更加准确的。
2、SVM既可以解决分类问题,又可以解决回归问题,原理整体相似,不过也稍有不同。
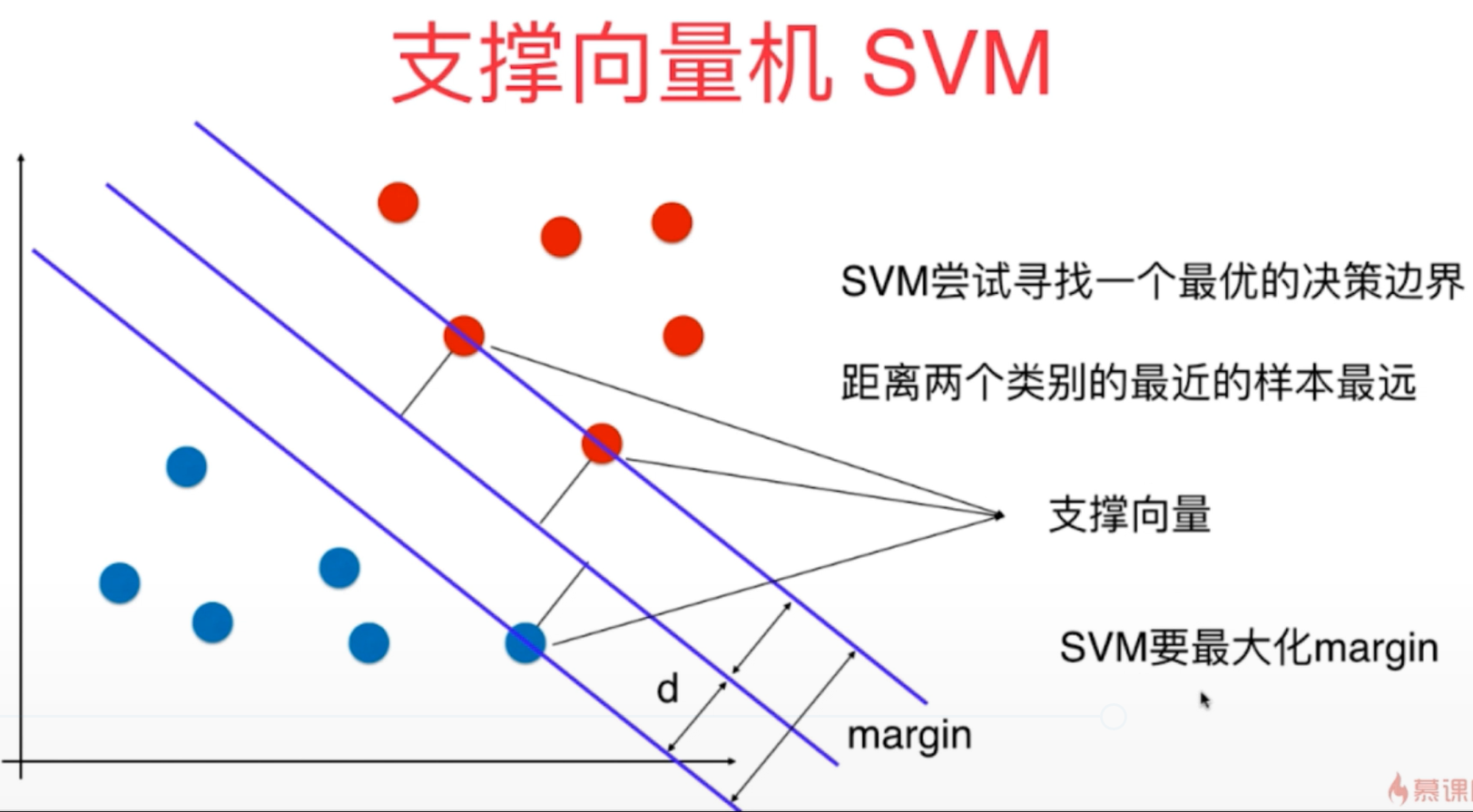
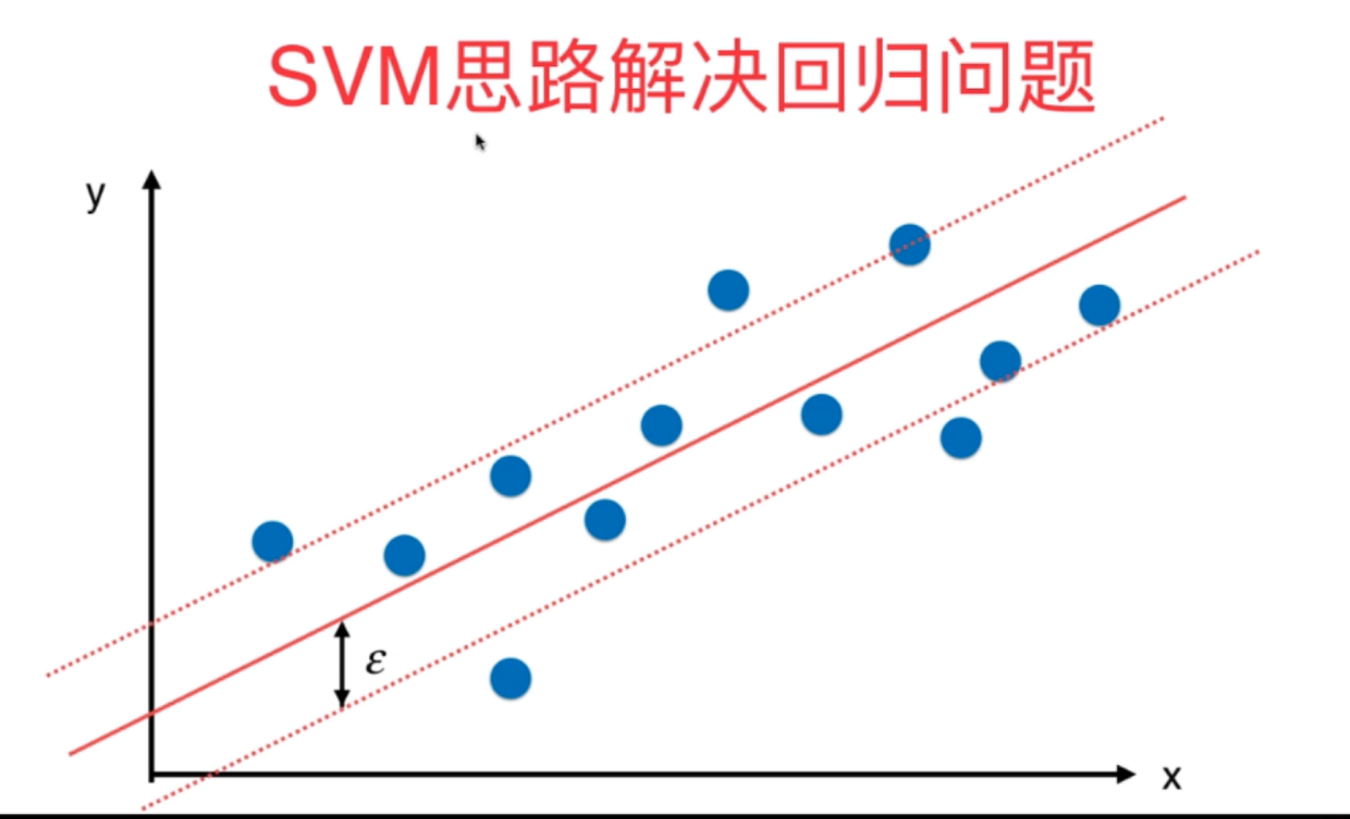
在sklearn章调用SVM算法的代码实现如下所示:
#(一)sklearn中利用SVM算法解决分类问题
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
d=datasets.load_iris()
x=d.data
y=d.target
x=x[y<2,:2]
y=y[y<2]
print(x)
print(y)
plt.figure()
plt.scatter(x[y==0,0],x[y==0,1],color="r")
plt.scatter(x[y==1,0],x[y==1,1],color="g")
plt.show()
#进行数据据标准化处理(线性方式)
from sklearn.preprocessing import StandardScaler
s1=StandardScaler()
s1.fit(x)
x_standard=s1.transform(x)
print(np.hstack([x,x_standard]))
#导入sklearn中SVM的线性分类算法LinearSVC
from sklearn.svm import LinearSVC
s11=LinearSVC(C=1e9) #多分类问题的实现需要提交参数penalty=l1/l2(正则化方式)以及multi_class=ovo/ovr(采用何种方式多分类训练)
s11.fit(x_standard,y)
def plot_decision_boundary(model,axis):
x0,x1=np.meshgrid(
np.linspace(axis[0],axis[1],int((axis[1]-axis[0])*100)).reshape(-1,1),
np.linspace(axis[2],axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1,1)
)
x_new=np.c_[x0.ravel(),x1.ravel()]
y_pre=model.predict(x_new)
zz=y_pre.reshape(x0.shape)
from matplotlib.colors import ListedColormap
cus=ListedColormap(["#EF9A9A","#FFF59D","#90CAF9"])
plt.contourf(x0,x1,zz,cmap=cus)
plot_decision_boundary(s11,axis=([-3,3,-3,3]))
plt.scatter(x_standard[y==0,0],x_standard[y==0,1],color="r")
plt.scatter(x_standard[y==1,0],x_standard[y==1,1],color="g")
plt.show()
print(s11.coef_)
print(s11.intercept_)
#输出svc函数的决策边界
def plot_svc_decision_boundary(model,axis):
x0,x1=np.meshgrid(
np.linspace(axis[0],axis[1],int((axis[1]-axis[0])*100)).reshape(-1,1),
np.linspace(axis[2],axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1,1)
)
x_new=np.c_[x0.ravel(),x1.ravel()]
y_pre=model.predict(x_new)
zz=y_pre.reshape(x0.shape)
from matplotlib.colors import ListedColormap
cus=ListedColormap(["#EF9A9A","#FFF59D","#90CAF9"])
plt.contourf(x0,x1,zz,cmap=cus)
w=model.coef_[0]
b=model.intercept_[0]
x1=np.linspace(axis[0],axis[1],200)
upy=-w[0]*x1/w[1]-b/w[1]+1/w[1]
downy=-w[0]*x1/w[1]-b/w[1]-1/w[1]
upindex=((upy>axis[2])&(upy<axis[3]))
downindex = ((downy > axis[2]) & (downy < axis[3]))
plt.plot(x1[upindex],upy[upindex],"r")
plt.plot(x1[downindex],downy[downindex],"g")
plot_svc_decision_boundary(s11,axis=([-3,3,-3,3]))
plt.scatter(x_standard[y==0,0],x_standard[y==0,1],color="r")
plt.scatter(x_standard[y==1,0],x_standard[y==1,1],color="g")
plt.show() #sklearn中对于非线性数据的svm应用(多项式应用方式)
#1利用管道pipeline来进行多项式核函数的SVM算法
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
x,y=datasets.make_moons(noise=0.05,random_state=666) #生成数据默认为100个数据样本
print(x.shape)
print(y.shape)
plt.figure()
plt.scatter(x[y==0,0],x[y==0,1],color="r")
plt.scatter(x[y==1,0],x[y==1,1],color="g")
plt.show()
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC
from sklearn.pipeline import Pipeline
def polyniomailSVC(degree,C=1.0):
return Pipeline([("poly",PolynomialFeatures(degree=degree)),
("std_scaler",StandardScaler()),
("LinearSVC",LinearSVC(C=C))
]) p=polyniomailSVC(degree=3)
p.fit(x,y)
plot_decision_boundary(p,axis=([-1,2.5,-1,1.5]))
plt.scatter(x[y==0,0],x[y==0,1],color="r")
plt.scatter(x[y==1,0],x[y==1,1],color="g")
plt.show()
#2直接利用sklearn中自带的多项式核函数SVM算法,主要的参数kernel="poly"
from sklearn.svm import SVC
def polynomialkernelSVC(degree,C=1.0):
return Pipeline(
[
("std_canler",StandardScaler()),
("kernelsvc",SVC(kernel="poly",degree=degree,C=C))
]
)
p1=polynomialkernelSVC(degree=3)
p1.fit(x,y)
plot_decision_boundary(p1,axis=([-1,2.5,-1,1.5]))
plt.scatter(x[y==0,0],x[y==0,1],color="r")
plt.scatter(x[y==1,0],x[y==1,1],color="g")
plt.show()
#直观理解高斯核函数
import numpy as np
import matplotlib.pyplot as plt
x=np.arange(-4,5,1)
y=np.array((x>=-2)&(x<=2),dtype="int")
print(x)
print(y)
plt.figure()
plt.scatter(x[y==0],[0]*len(x[y==0]),color="r")
plt.scatter(x[y==1],[0]*len(x[y==1]),color="g")
plt.show()
def gauss(x,y):
gamma=1
return np.exp(-gamma*(x-y)**2)
l1,l2=-1,1
x_new=np.empty((len(x),2))
for i ,data in enumerate(x):
x_new[i,0]=gauss(data,l1)
x_new[i,1]=gauss(data,l2)
plt.scatter(x_new[y==0,0],x_new[y==0,1],color="r")
plt.scatter(x_new[y==1,0],x_new[y==1,1],color="g")
plt.show()
#调用sklearn中的高斯核函数RBF核(超参数主要是gamma)
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
x,y=datasets.make_moons(noise=0.1,random_state=666) #生成数据默认为100个数据样本
print(x.shape)
print(y.shape)
plt.figure()
plt.scatter(x[y==0,0],x[y==0,1],color="r")
plt.scatter(x[y==1,0],x[y==1,1],color="g")
plt.show()
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test=train_test_split(x,y,random_state=666)
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
from sklearn.pipeline import Pipeline
def RBFkernelSVC(gamma):
return Pipeline([
("std",StandardScaler()),
("svc",SVC(kernel="rbf",gamma=gamma))
])
sv=RBFkernelSVC(gamma=1)
sv.fit(x_train,y_train)
plot_decision_boundary(sv,axis=([-1.5,2.5,-1,1.5]))
plt.scatter(x[y==0,0],x[y==0,1],color="r")
plt.scatter(x[y==1,0],x[y==1,1],color="g")
plt.show()
print(sv.score(x_test,y_test))
from sklearn import datasets
d=datasets.load_iris()
x=d.data
y=d.target
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test=train_test_split(x,y,random_state=666)
sv=RBFkernelSVC(gamma=10)
sv.fit(x_train,y_train)
print(sv.score(x_test,y_test)) #(二)sklearn中利用SVM算法解决回归问题(epsilon为重要的超参数)
from sklearn import datasets
d=datasets.load_boston()
x=d.data
y=d.target
from sklearn.preprocessing import StandardScaler
s1=StandardScaler()
s1.fit(x)
x=s1.transform(x)
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test=train_test_split(x,y,random_state=666)
from sklearn.svm import LinearSVR
from sklearn.svm import SVR
from sklearn.preprocessing import StandardScaler
def StandardLinearSVR(epsilon):
return Pipeline([
("std",StandardScaler()),
("svr",LinearSVR(epsilon=epsilon))
])
sv=LinearSVR()
param_grid=[{
"epsilon":[i for i in np.arange(0,10,0.001)]
}]
from sklearn.model_selection import GridSearchCV
grid_search=GridSearchCV(sv,param_grid,n_jobs=-1,verbose=0)
grid_search.fit(x_train,y_train)
print(grid_search.best_params_)
print(grid_search.best_score_)
def polyniomailSVR(degree,C,epsilon):
return Pipeline([("poly",PolynomialFeatures(degree=degree)),
("std_scaler",StandardScaler()),
("LinearSVC",LinearSVR(C=C,epsilon=epsilon))
])
p1=polyniomailSVR(degree=2,C=1,epsilon=0.5)
p1.fit(x_train,y_train)
print(p1.score(x_test,y_test)) def polynomialkernelSVR(degree,coefo,epsilon):
return Pipeline(
[
("std_canler",StandardScaler()),
("kernelsvc",SVR(kernel="poly",degree=degree,coef0=coefo,epsilon=epsilon))
]
)
p1=polynomialkernelSVR(degree=3,C=1,epsilon=0.1)
p1.fit(x_train,y_train)
print(p1.score(x_test,y_test)) def RBFkernelSVR(gamma,epsilon):
return Pipeline([
("std",StandardScaler()),
("svc",SVR(kernel="rbf",gamma=gamma,epsilon=epsilon))
])
p2=RBFkernelSVR(gamma=0.05,epsilon=0.1)
p2.fit(x_train,y_train)
print(p2.score(x_test,y_test)) 运行结果如下所示:
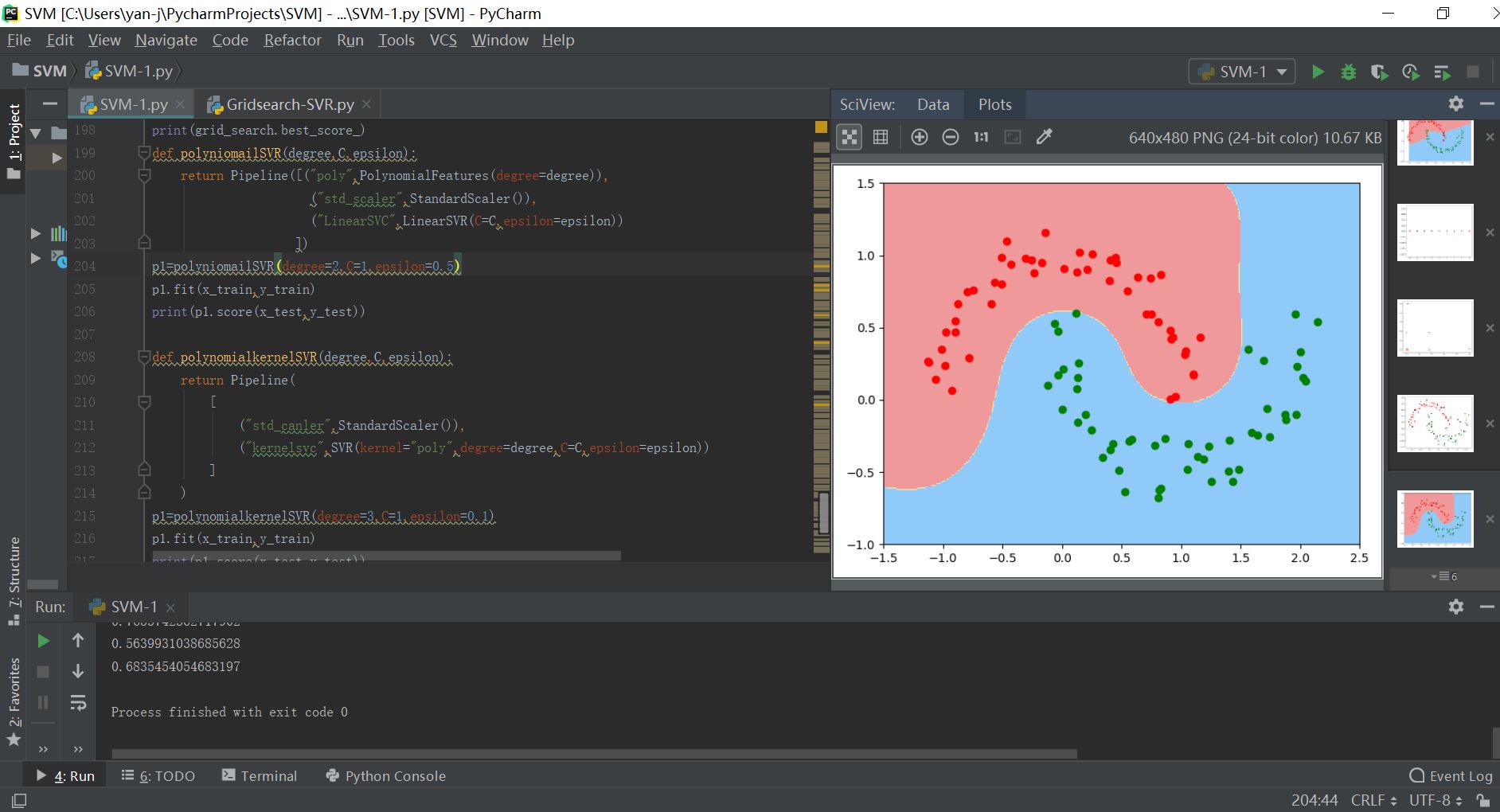
sklearn调用SVM算法的更多相关文章
- sklearn调用分类算法的评价指标
sklearn分类算法的评价指标调用#二分类问题的算法评价指标import numpy as npimport matplotlib.pyplot as pltimport pandas as pdf ...
- sklearn中调用PCA算法
sklearn中调用PCA算法 PCA算法是一种数据降维的方法,它可以对于数据进行维度降低,实现提高数据计算和训练的效率,而不丢失数据的重要信息,其sklearn中调用PCA算法的具体操作和代码如下所 ...
- SVM算法
本文主要介绍支持向量机理论推导及其工程应用. 1 基本介绍 支持向量机算法是一个有效的分类算法,可用于分类.回归等任务,在传统的机器学习任务中,通过人工构造.选择特征,然后使用支持向量机作为训练器,可 ...
- SVM算法简单应用
第一部分:线性可分 通俗解释:可以用一条直线将两类分隔开来 一个简单的例子,直角坐标系中有三个点,A,B点为0类,C点为1类: from sklearn import svm # 三个点 x = [[ ...
- 一步步教你轻松学支持向量机SVM算法之理论篇1
一步步教你轻松学支持向量机SVM算法之理论篇1 (白宁超 2018年10月22日10:03:35) 摘要:支持向量机即SVM(Support Vector Machine) ,是一种监督学习算法,属于 ...
- svm算法介绍
在一个理想的分类当中,我们想要用一个超平面来将正类样本和负类样本划分开来.这个超平面的方程为 $\mathbf{w}^T\mathbf{x}+b=0$ 我们希望这个超平面能够使得划分更加的鲁棒,在图形 ...
- 【转】 SVM算法入门
课程文本分类project SVM算法入门 转自:http://www.blogjava.net/zhenandaci/category/31868.html (一)SVM的简介 支持向量机(Supp ...
- SVM算法入门
转自:http://blog.csdn.net/yangliuy/article/details/7316496SVM入门(一)至(三)Refresh 按:之前的文章重新汇编一下,修改了一些错误和不当 ...
- 转载:scikit-learn学习之SVM算法
转载,http://blog.csdn.net/gamer_gyt 目录(?)[+] ========================================================= ...
随机推荐
- 【C语言】输入5个整数并按输入顺序逆序输出
#include <stdio.h> int main() { ],i; printf("请输入5个整数:\n"); ;i<;i++) scanf("% ...
- ABC156D
[题目链接]https://atcoder.jp/contests/abc156/tasks/abc156_d 简单数论问题,题意就是有n个数,不能组成a与b个数,问有多少种组合方式 那就是C(n,1 ...
- ASP.NET(C#) Json序列化反序列化帮助类Jsonhelper
原文地址:https://ken.io/note/csharp-asp.net-jsonhelper using System; using System.Collections.Generic; u ...
- cglib用法
CGLib动态代理的介绍及用法(单回调.多回调.不处理.固定值.懒加载) 参照: https://blog.csdn.net/difffate/article/details/70552056 前面介 ...
- spring boot properties文件与yaml文件的区别
编写是没有提示的话在pom中添加依赖,如下: <!-- 配置文件处理器 编写配置时会有提示 --> <dependency> <groupId>org.spring ...
- CentOS7 安装 OpenCV 的一些问题解决办法
由于强迫症,实在受不了root权限的旧gcc才能使用boost而普通权限却是最新版gcc,经过一番折腾后,终于把配置全部弄好了,实际上就只需要把新版gcc的各个文件放到系统找到旧gcc的地方,并建立新 ...
- [运维] 如何解决 nginx: [emerg] bind() to 0.0.0.0:80 failed (13: Permission denied)
环境: 虚拟机 linux centos 7 64 当时正在配置 nginx , 由于解压后的 nginx 默认安装位置是在 /usr/local/ 目录下, 而这个目录是 root 用户才有权限操作 ...
- JDBC连接MySql例子
1.注册MySql连接驱动 2.设置连接MySql连接字符串.用户名和密码 3.获取数据库连接 代码如下: // 加载驱动 Class.forName("com.mysql.jdbc.Dri ...
- PHP的isset()、is_null、empty()使用总结
这几个变量判断函数在PHP开发中用的其实挺多的,而且粗看上去都差不多,但其实还是有不少的区别的,如果搞不清楚,也许就会遗留一些潜在的bug, 包括我自已也遇到过这样的坑,比如有一次我就遇到过用empt ...
- 工具 - PyCharm相关
Ctrl + Q查看Documentation Ctrl + Alt + L 格式化代码 """""" + enter就可以自动生成DocS ...
