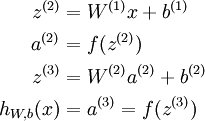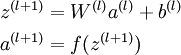神经网络,前向传播FP和反向传播BP
1 神经网络
神经网络就是将许多个单一“神经元”联结在一起,这样,一个“神经元”的输出就可以是另一个“神经元”的输入。例如,下图就是一个简单的神经网络:
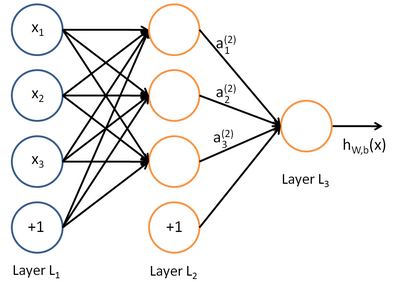
我们使用圆圈来表示神经网络的输入,标上“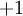 ”的圆圈被称为偏置节点,也就是截距项。神经网络最左边的一层叫做输入层,最右的一层叫做输出层(本例中,输出层只有一个节点)。中间所有节点组成的一层叫做隐藏层,因为我们不能在训练样本集中观测到它们的值。同时可以看到,以上神经网络的例子中有3个输入单元(偏置单元不计在内),3个隐藏单元及一个输出单元。
”的圆圈被称为偏置节点,也就是截距项。神经网络最左边的一层叫做输入层,最右的一层叫做输出层(本例中,输出层只有一个节点)。中间所有节点组成的一层叫做隐藏层,因为我们不能在训练样本集中观测到它们的值。同时可以看到,以上神经网络的例子中有3个输入单元(偏置单元不计在内),3个隐藏单元及一个输出单元。
我们用 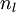 来表示网络的层数,本例中
来表示网络的层数,本例中 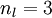 ,我们将第
,我们将第  层记为
层记为 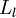 ,于是
,于是 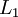 是输入层,输出层是
是输入层,输出层是 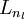 。本例神经网络有参数
。本例神经网络有参数 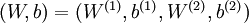 ,其中
,其中 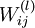 (下面的式子中用到)是第
(下面的式子中用到)是第  层第
层第  单元与第
单元与第  层第
层第  单元之间的联接参数(其实就是连接线上的权重,注意标号顺序),
单元之间的联接参数(其实就是连接线上的权重,注意标号顺序), 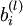 是第
是第  层第
层第  单元的偏置项。因此在本例中,
单元的偏置项。因此在本例中, 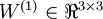 ,
, 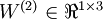 。注意,没有其他单元连向偏置单元(即偏置单元没有输入),因为它们总是输出
。注意,没有其他单元连向偏置单元(即偏置单元没有输入),因为它们总是输出 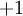 。同时,我们用
。同时,我们用 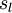 表示第
表示第  层的节点数(偏置单元不计在内)。
层的节点数(偏置单元不计在内)。
2 前向传播FP
我们用 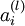 表示第
表示第  层第
层第  单元的激活值(输出值)。当
单元的激活值(输出值)。当 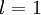 时,
时, 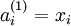 ,也就是第
,也就是第  个输入值(输入值的第
个输入值(输入值的第  个特征)。对于给定参数集合
个特征)。对于给定参数集合 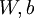 ,我们的神经网络就可以按照函数
,我们的神经网络就可以按照函数 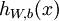 来计算输出结果。本例神经网络的计算步骤如下:
来计算输出结果。本例神经网络的计算步骤如下:
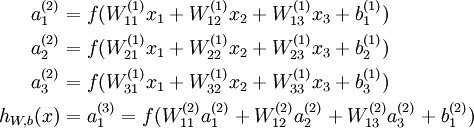
我们用 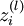 表示第
表示第  层第
层第  单元输入加权和(包括偏置单元),比如,
单元输入加权和(包括偏置单元),比如, 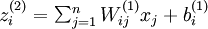 ,则
,则 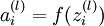 。
。
这样我们就可以得到一种更简洁的表示法。这里我们将激活函数 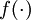 扩展为用向量(分量的形式)来表示,即
扩展为用向量(分量的形式)来表示,即 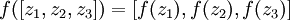 ,那么,上面的等式可以更简洁地表示为:
,那么,上面的等式可以更简洁地表示为:
我们将上面的计算步骤叫作前向传播。回想一下,之前我们用 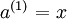 表示输入层的激活值,那么给定第
表示输入层的激活值,那么给定第  层的激活值
层的激活值 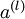 后,第
后,第  层的激活值
层的激活值 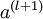 就可以按照下面步骤计算得到:
就可以按照下面步骤计算得到:
将参数矩阵化,使用矩阵-向量运算方式,我们就可以利用线性代数的优势对神经网络进行快速求解。
目前为止,我们讨论了一种神经网络,我们也可以构建另一种结构的神经网络(这里结构指的是神经元之间的联接模式),也就是包含多个隐藏层的神经网络。最常见的一个例子是 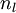 层的神经网络,第
层的神经网络,第 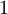 层是输入层,第
层是输入层,第 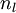 层是输出层,中间的每个层
层是输出层,中间的每个层  与层
与层  紧密相联。这种模式下,要计算神经网络的输出结果,我们可以按照之前描述的等式,按部就班,进行前向传播,逐一计算第
紧密相联。这种模式下,要计算神经网络的输出结果,我们可以按照之前描述的等式,按部就班,进行前向传播,逐一计算第 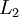 层的所有激活值,然后是第
层的所有激活值,然后是第 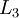 层的激活值,以此类推,直到第
层的激活值,以此类推,直到第 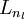 层。这是一个前馈神经网络的例子,因为这种联接图没有闭环或回路。
层。这是一个前馈神经网络的例子,因为这种联接图没有闭环或回路。
神经网络也可以有多个输出单元。比如,下面的神经网络有两层隐藏层: 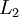 及
及 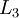 ,输出层
,输出层 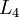 有两个输出单元。
有两个输出单元。
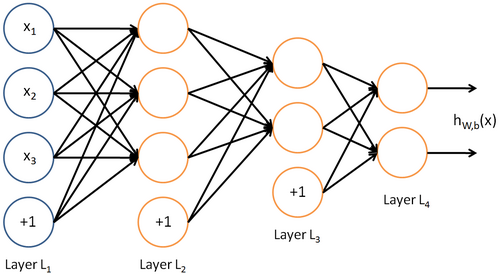
要求解这样的神经网络,需要样本集 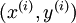 ,其中
,其中 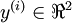 。如果你想预测的输出是多个的,那这种神经网络很适用。(比如,在医疗诊断应用中,患者的体征指标就可以作为向量的输入值,而不同的输出值
。如果你想预测的输出是多个的,那这种神经网络很适用。(比如,在医疗诊断应用中,患者的体征指标就可以作为向量的输入值,而不同的输出值 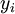 可以表示不同的疾病存在与否。)
可以表示不同的疾病存在与否。)
3 反向传播BP
前面用初始化的联结权重计算的输出层值和实际值肯定会有很大的偏差,我们需要对连接权重进行优化,此时就需要使用反向传播算法。
现在假设经过前向传播算法计算的某个输出值为ykyk,表示输出层的第kk个输出,而其实际的值为tktk(训练样本的标签值是已知的,不然怎么训练)。那么误差函数定义如下:

后向传播算法是通过梯度下降的方法对联结权重进行优化,所以需要计算误差函数对联结权重的偏导数。
1.计算总误差
总误差:(square error)
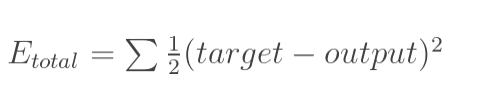
但是有两个输出,所以分别计算o1和o2的误差,总误差为两者之和:


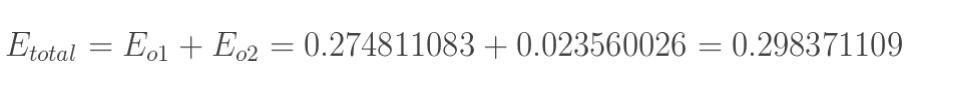
2.隐含层---->输出层的权值更新:
以权重参数w5为例,如果我们想知道w5对整体误差产生了多少影响,可以用整体误差对w5求偏导求出:(链式法则)

下面的图可以更直观的看清楚误差是怎样反向传播的:

神经网络,前向传播FP和反向传播BP的更多相关文章
- 深度学习——前向传播算法和反向传播算法(BP算法)及其推导
1 BP算法的推导 图1 一个简单的三层神经网络 图1所示是一个简单的三层(两个隐藏层,一个输出层)神经网络结构,假设我们使用这个神经网络来解决二分类问题,我们给这个网络一个输入样本,通过前向运算得到 ...
- 浅层神经网络 反向传播推导:MSE softmax
基础:逻辑回归 Logistic 回归模型的参数估计为什么不能采用最小二乘法? logistic回归模型的参数估计问题不能“方便地”定义“误差”或者“残差”. 对单个样本: 第i层的权重W[i]维度的 ...
- BP神经网络反向传播之计算过程分解(详细版)
摘要:本文先从梯度下降法的理论推导开始,说明梯度下降法为什么能够求得函数的局部极小值.通过两个小例子,说明梯度下降法求解极限值实现过程.在通过分解BP神经网络,详细说明梯度下降法在神经网络的运算过程, ...
- 关于 RNN 循环神经网络的反向传播求导
关于 RNN 循环神经网络的反向传播求导 本文是对 RNN 循环神经网络中的每一个神经元进行反向传播求导的数学推导过程,下面还使用 PyTorch 对导数公式进行编程求证. RNN 神经网络架构 一个 ...
- BP(back propagation)反向传播
转自:http://www.zhihu.com/question/27239198/answer/89853077 机器学习可以看做是数理统计的一个应用,在数理统计中一个常见的任务就是拟合,也就是给定 ...
- [2] TensorFlow 向前传播算法(forward-propagation)与反向传播算法(back-propagation)
TensorFlow Playground http://playground.tensorflow.org 帮助更好的理解,游乐场Playground可以实现可视化训练过程的工具 TensorFlo ...
- CS231n课程笔记翻译5:反向传播笔记
译者注:本文智能单元首发,译自斯坦福CS231n课程笔记Backprop Note,课程教师Andrej Karpathy授权翻译.本篇教程由杜客翻译完成,堃堃和巩子嘉进行校对修改.译文含公式和代码, ...
- 实现属于自己的TensorFlow(二) - 梯度计算与反向传播
前言 上一篇中介绍了计算图以及前向传播的实现,本文中将主要介绍对于模型优化非常重要的反向传播算法以及反向传播算法中梯度计算的实现.因为在计算梯度的时候需要涉及到矩阵梯度的计算,本文针对几种常用操作的梯 ...
- 【cs231n】反向传播笔记
前言 首先声明,以下内容绝大部分转自知乎智能单元,他们将官方学习笔记进行了很专业的翻译,在此我会直接copy他们翻译的笔记,有些地方会用红字写自己的笔记,本文只是作为自己的学习笔记.本文内容官网链接: ...
随机推荐
- H5新特性总结
Web前端最新的官方标准无疑就是es6和H5了,es6之前已经说过了(多是一些语法糖),现在来总结一下H5给我们来了哪些新“朋友”吧~ 1.video/radio 视频/音频 2.canvas 绘画 ...
- P1282 多米诺骨牌
P1282 多米诺骨牌 题目描述 多米诺骨牌有上下2个方块组成,每个方块中有1~6个点.现有排成行的 上方块中点数之和记为S1,下方块中点数之和记为S2,它们的差为|S1-S2|.例如在图8-1中,S ...
- Bash基本功能
bash的基本功能 作者:尹正杰 版权声明:原创作品,谢绝转载!否则将追究法律责任. 欢迎加入: 高级运维工程师之路 598432640 一.历史命令和命令补全 1.历 ...
- FastDFS与Nginx的搭建及遇到的问题
1.1 FastDFS与Nginx的搭建 可以使用一台虚拟机来模拟,只有一个Tracker.一个Storage服务. 配置nginx访问图片. 1.1.1 搭建步骤 第一步:把fastDFS需要 ...
- JavaSE学习总结(五)——封装,继承,多态很简单
java面向对象的三大特性是:封装.继承与多态,是面向对象编程的核心. 一.封装 简单说封装就是将同一类事物的特性与功能包装在一起,对外暴露调用的接口. 封装:封装也称信息隐藏,是指利用抽象数据类型把 ...
- centOS7环境下安装jdk1.8
首先下载jdk1.8 去官网下载jdk:http://www.oracle.com/technetwork/java/javase/downloads/jdk8-downloads-2133151. ...
- hbase记录-修改压缩格式
在业务空闲的时候修改压缩格式 先测试 ---测试表create 'test', { NAME => 'c',VERSIONS => 1}desc 'test'disable 'test'a ...
- Java编程思想 学习笔记6
六.访问权限控制 访问控制(或隐藏具体实现)与“最初的实现并不恰当”有关. 如何把变动的事物与保持不变的事物区分开来,这是面向对象设计中的一个基本问题. 为了解决这一问题,Java提供了访问权限修饰词 ...
- mssql拿webshell的方法
首先检测下MSSQL数据库的用户权限,一般有两种,一种是SA权限,这种权限很大,还有一种是DB_OWNER权限,这个权限赋给用户一些对数据库的修改.删除.新增数据库表,执行部分存储过程的权限.但是涉及 ...
- comfirm和prompt的区别
comfirm和prompt的区别. <html> <title>测试页面</title> <head> </head> <body& ...