Educational Codeforces Round 47 (Rated for Div. 2) 题解

题目链接：http://codeforces.com/contest/1009

A. Game Shopping 题目：

题意：有n件物品，你又m个钱包，每件物品的价格为ai，每个钱包里的前为bi。你站在第一件物品前，如果你的第一个钱包能购买这件物品，你第一个钱包的钱直接消失（就相当于你是用第一个钱包里的所有钱购买了这件物品，不会找钱），如果无法购买那么就跳到下一件物品，以此类推，问你总共能购买多少件物品。

思路：直接模拟即可。

代码如下：

 #include <bits/stdc++.h>
 using namespace std;

 const int maxn = ;
 int n, m, ans;
 int a[maxn], b[maxn];

 int main() {
     cin >>n >>m;
     for(int i = ; i < n; i++) {
         cin >>a[i];
     }
     for(int i = ; i < m; i++) {
         cin >>b[i];
     }
     for(int i = , j = ; i < n ; i++) {
         if(j >= m) break;
         if(b[j] >= a[i]) {
             j++;
             ans++;
         }
     }
     cout <<ans <<endl;
     return ;
 }

B. Minimum Ternary String  题目：

题意：给你一个只含012的串，0可以和1交换，1可以和2交换，0不可以和2交换，问进行多次交换后字典序最小的串是啥。

思路：因为1可以和02交换，所以要想字典序最小1必须全在2前面；2不能和0换，所以2和0的相对位置不变。故此题的思路就是将第一个2前的的所有0放在最前面，然后紧跟所有的1，后面的2和0就按照原顺序即可。方法1：暴力。方法2：借用vetctor。

代码如下：

 //方法一
 //#include <bits/stdc++.h>
 //using namespace std;
 //
 //const int maxn = 1e5 + 7;
 //int a[maxn];
 //string s, t;
 //
 //int main() {
 //    cin >>s;
 //    int cnt1 = 0, cnt2 = 0, cnt3 = 0;
 //    int pos = -1;
 //    for(int i = 0; i <s.size(); i++) {
 //        if(s[i] != '0') {
 //            pos = i;
 //            break;
 //        }
 //    }
 //    for(int i = s.size() - 1; i >= pos; i--) {
 //        if(s[i] == '0') {
 //            cnt1++;
 //            if(cnt3 > 0) {
 //                for(int j = 0; j < cnt3; j++) {
 //                    t += '2';
 //                }
 //                cnt3 = 0;
 //            }
 //        } else if(s[i] == '1') {
 //            cnt2++;
 //        } else if(s[i] == '2') {
 //            cnt3++;
 //            if(cnt1 > 0) {
 //                for(int j = 0; j <cnt1; j++) {
 //                    t += '0';
 //                }
 //                cnt1 = 0;
 //            }
 //        }
 //    }
 //    for(int i = 0; i < cnt3; i++) {
 //        t += '2';
 //    }
 //    for(int i = 0; i <cnt2; i++) {
 //        t += '1';
 //    }
 //    for(int i = 0; i < pos; i++) {
 //        t += '0';
 //    }
 //    for(int i = 0; i < cnt1; i++) {
 //        t += '0';
 //    }
 //    reverse(t.begin(), t.end());
 //    cout <<t <<endl;
 //    return 0;
 //}

 //方法二
 #include <bits/stdc++.h>
 using namespace std;

 string s;
 vector<char> v;

 int main() {
     cin >>s;
     int cnt = ;
     for(int i = ; i < s.size(); i++) {
         if(s[i] == '') cnt++;
         else v.push_back(s[i]);
     }
     int flag = ;
     for(int i = ; i < v.size(); i++) {
         if(v[i] == '' && !flag) {
             while(cnt--) {
                 cout<<"";
             }
             cout <<"";
             flag = ;
         } else {
             cout <<v[i];
         }
     }
     //可能没有0、1，所以要在这里输出一遍
     for(int i = ; i <cnt; i++) {
         cout <<"";
     }
     cout <<endl;
     return ;
 }

C. Annoying Present 题目：

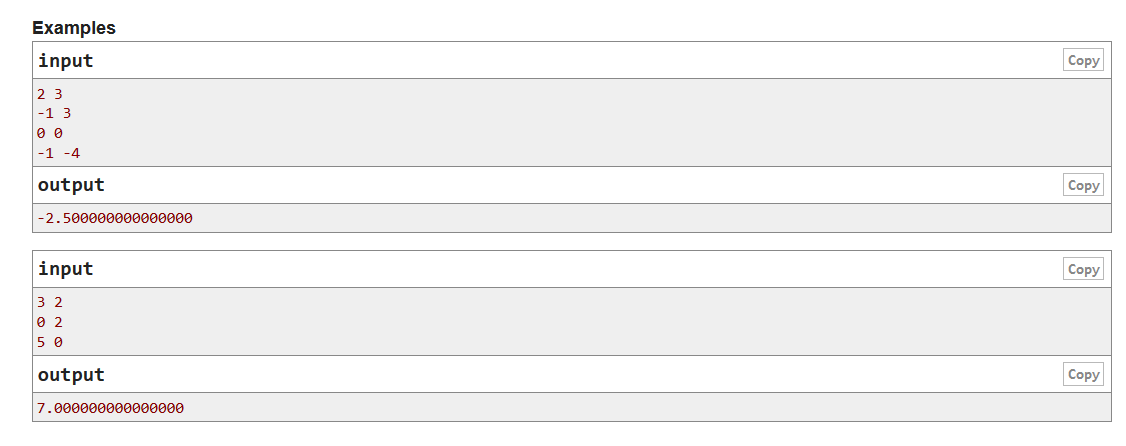
题意：有n个元素，初始为0，进行m次操作，每次操作给你x和d，你选择一个i，然后对每个元素（记为j，包括i）进行操作ai+x+d*dist(i,j)，问最后所有元素的最大平均值是多少。

思路：这个就是个贪心+公式题。这题的贪心方法是当d>0时，i选择最左（最右都可以，因为dist(i,j)是一样的，最后是算平均值，所有加在哪个元素上是没有区别的；当d<0时，选择最中间，此处要将n分奇偶，因为奇数和偶数是有所区别的。当推出这些之后会发现这题就是个等差数列求和，注意会爆int，比赛的时候就是被这个点坑死。ps.赛后这题是被hack人数最多的，本场hack数排第一的大佬就是这题hack了600多人，第一个坑点就是求和不能用double，会有精度损失，第二个坑点就是不要先除，要先求和再除。

代码实现如下：

 #include <bits/stdc++.h>
 using namespace std;

 typedef long long ll;
 ll n, m, x, d, ans;

 int main() {
     scanf("%I64d%I64d", &n, &m);
     while(m--) {
         scanf("%I64d%I64d", &x, &d);
         ans += x * n;
         if(d > ) {
             ans += (n - ) * n /  * d;
         }  else {
             if(n & ) ans += (n /  + ) * (n / ) * d;
             else ans += (n / ) * (n / ) * d;
         }
     }
     printf("%.8f\n", ans * 1.0 / n);
     return ;
 }

D. Relatively Prime Graph 题目：

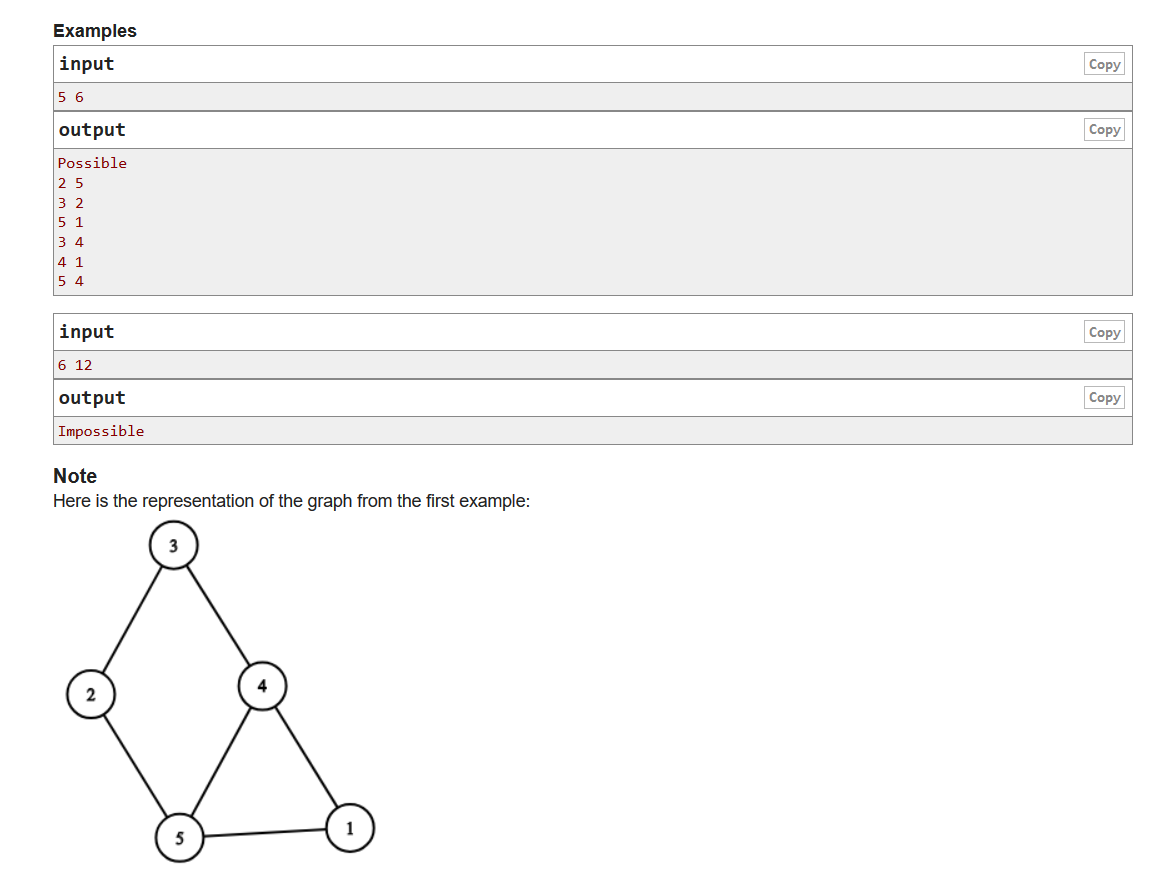
题意：构造一个只有n个点m条边的联通图，且相邻节点的编号要互质。

思路：当m<n-1时，由图联通知至少需要n-1条边，因此此处为impossible。1与所有的数都互质，所以此处保证了联通性。因为只需要m条边，由欧拉函数可以证得此题暴力的复杂度是稍大于O(m),我只会估算，具体证明暂时不会……因此此题可以暴力水过。

代码如下：

 #include <cmath>
 #include <cstdio>
 #include <iostream>
 #include <algorithm>
 using namespace std;

 const int maxn = 1e5 + ;
 int n, m, t;

 struct node {
     int x, y;
 }edge[maxn];

 int main() {
     cin >>n >>m;
     if(n -  > m) {
         puts("Impossible");
         return ;
     }
     int flag = ;
     for(int i = ; i <= n; i++) {
         for(int j = i + ; j <= n; j++) {
             if( __gcd(i, j) == ) {
                 edge[t].x = i;
                 edge[t].y = j;
                 t++;
                 if(t >= m) {
                     flag = ;
                     break;
                 }
             }
         }
         if(flag) break;
     }
     if(flag) {
         puts("Possible");
         for(int i = ; i < m; i++) {
             cout <<edge[i].x <<" " <<edge[i].y <<endl;
         }
     } else {
         puts("Impossible");
     }
     return ;
 }

---

赛后补题

E. Intercity Travelling 题目：

题意：Leha从数轴的0到n，中间的整数点都有可能有休息点也可能没有休息点。当你连续坐k站时，每两站间的疲劳值为a1,a2……ak，如果第k站有休息点，那么你可以在此处休息，然后接下来的站点的疲劳值又从a1开始，否则继续为ak+1。题目给你n和ai，每个站点有休息点的概率都是1/2，问你期望值*2^(n-1)的值。

思路：我们知道从0到1的疲劳值一定为a1，1到2的疲劳值为a1(1/2),a2(1/2)，括号里面为概率，当1有休息点时为a1，否则为a2；2到3的疲劳值为a1(1/2),a2(1/4),a3(1/4)……以此类推得到下图：

然后将他们加起来乘以2^（n-1)即可。ps.别用cin,cout，会T9，别问我怎么知道的！

代码实现如下：

 #include <bits/stdc++.h>
 using namespace std;

 typedef long long ll;
 const int mod = ;
 const int maxn = 1e6 + ;
 int n;
 ll ans;
 ll a[maxn], p[maxn];

 int main() {
     scanf("%d", &n);
     p[] = ;
     for(int i = ; i <= n; i++) {
         p[i] = p[i-] *  % mod;
     }
     for(int i = ; i <= n; i++) {
         scanf("%I64d", &a[i]);
     }
     ans = a[n];
     for(int i = ; i < n; i++) {
         ans = (ans + (a[i] * (p[n - i] + p[n - i - ] * (n - i) % mod) % mod) % mod) % mod;
     }
     printf("%I64d\n", ans);
     return ;
 }