第二十九篇 玩转数据结构——线段树（Segment Tree）

 

 

 

1.. 线段树引入

• 线段树也称为区间树
• 为什么要使用线段树：对于某些问题，我们只关心区间（线段）
• 经典的线段树问题：区间染色，有一面长度为n的墙，每次选择一段墙进行染色（染色允许覆盖），问：经过m次操作后，可以看见多少种颜色？再进一步，经过m次操作后，在区间[i, j]中可以看到多少种颜色？
• 上面的问题涉及到了两种操作，即，染色操作（更新区间）和查询操作（查询区间），可以使用数组来对问题进行描述，这两种操作的时间复杂度如下：
• 
• 由于通过数组来进行实现的时间复杂度达到了O(n)级别，因此，通过数组实现不是一个理想的选择，线段树比较适合解决这类问题
• 另一类经典问题：区间查询，查询一个区间[i, j]中的最大值、最小值或者区间数字之和等

2.. 线段树所要解决的问题

• 对于一个给定的区间：
• 更新：更新区间中的一个元素或者一个区间的值
• 查询：查询一个区间[i, j]中的最大值、最小值，或者区间中的数字之和等等，针对一个区间进行的各种统计查询操作。

3.. 什么是线段树

• 线段树大概长这个样子
• 
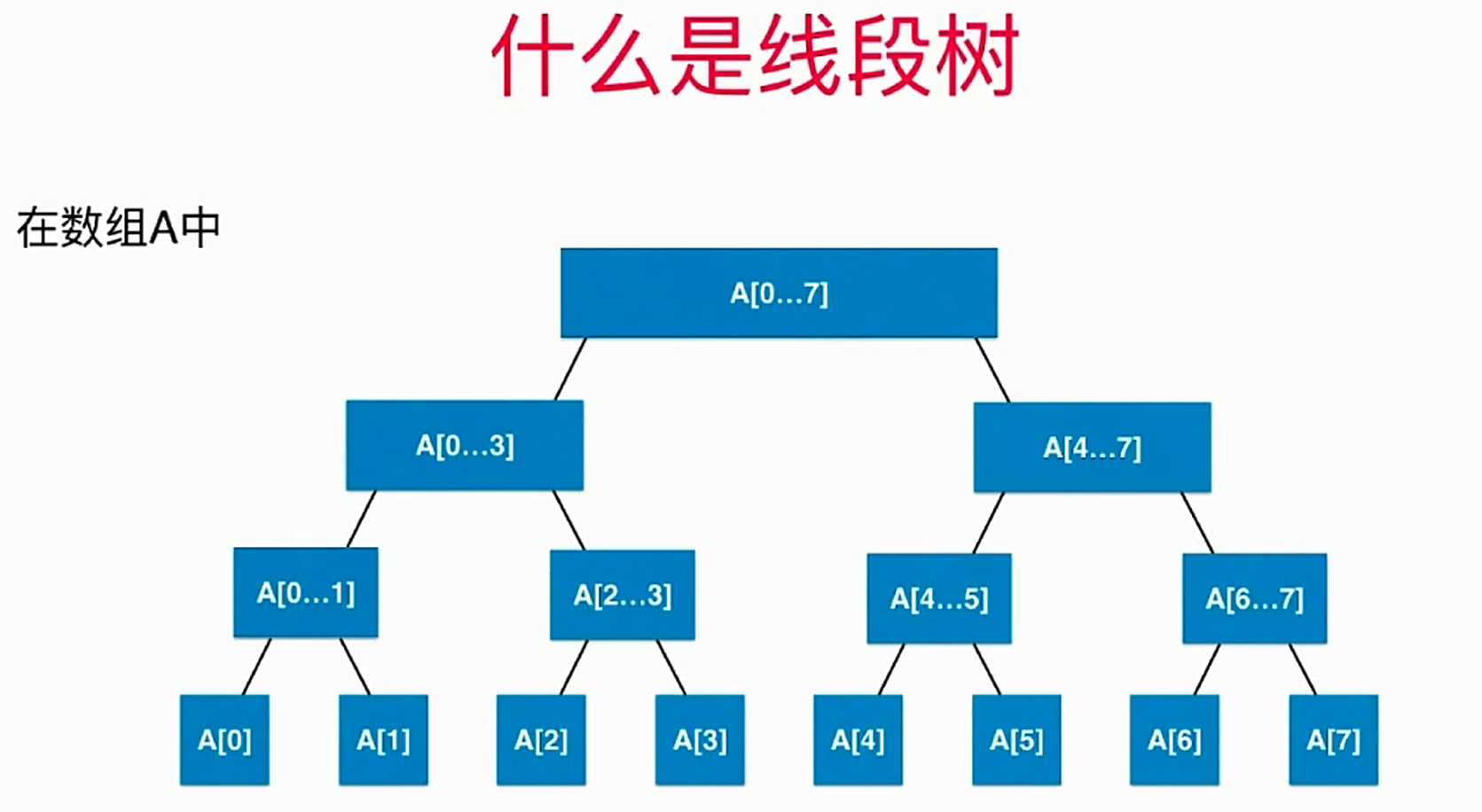
• 线段树的每个节点中存储的是某个区间的信息，以求和为例，线段树的每个节点中存储的就是某个区间的和，根节点中存储的就是整个区间的和，根节点向下，会将区间均分为两段，两端区间的和，分别存储在根节点的两个子节点中，再向下，依次类推，直至每个叶子节点，每个叶子节点只存储一个元素构成的区间
• 线段树不一定是一棵满二叉树，也不一定是一棵完全二叉树，但是，线段树是一棵平衡二叉树，如下：
• 
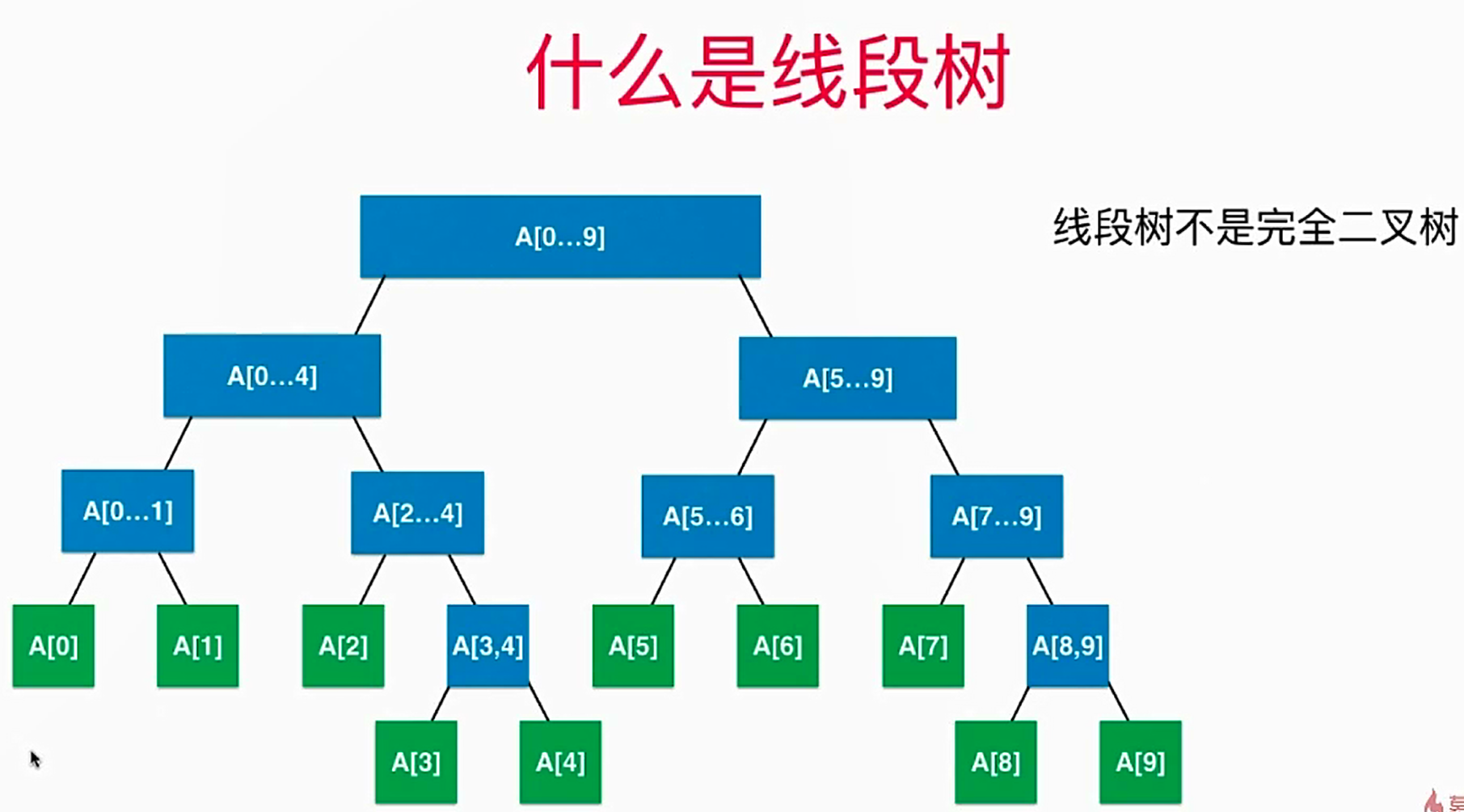
• "平衡二叉树"是指，二叉树的最大深度与最小深度之间的差，最大为1，由这个概念来看，"堆"，也是一棵平衡二叉树，"二分搜索树"就不一定是平衡二叉树。
• 用数组来表示线段树所需要的存储空间：
• 

4.. 实现线段树

• 实现线段树的业务逻辑

• public class SegmentTree<E> {
  
      private E[] data;
      private E[] tree;
      private Merger<E> merger;
  
      // 构造函数
      public SegmentTree(E[] arr, Merger<E> merger) {
  
          this.merger = merger;
  
          data = (E[]) new Object[arr.length];
          for (int i = 0; i < arr.length; i++) {
              data[i] = arr[i];
          }
  
          tree = (E[]) new Object[4 * arr.length];
          buildSegmentTree(0, 0, data.length - 1);
  
      }
  
      // 在treeIndex这个位置创建区间为[l...r]的线段树
      private void buildSegmentTree(int treeIndex, int l, int r) {
          if (l == r) {
              tree[treeIndex] = data[l];
              return;
          }
  
          int leftTreeIndex = leftChild(treeIndex);
          int rightTreeIndex = rightChild(treeIndex);
          int mid = l + (r - l) / 2;
  
          buildSegmentTree(leftTreeIndex, l, mid);
          buildSegmentTree(rightTreeIndex, mid + 1, r);
  
          tree[treeIndex] = merger.merge(tree[leftTreeIndex], tree[rightTreeIndex]);
      }
  
      public int getSize() {
          return data.length;
      }
  
      public E get(int index) {
          if (index < 0 || index >= data.length) {
              throw new IllegalArgumentException("Index is illegal.");
          }
          return data[index];
      }
  
      // 返回一个索引所表示的节点的左孩子的索引
      private int leftChild(int index) {
          return 2 * index + 1;
      }
  
      // 返回一个索引所表示的节点的右孩子的索引
      private int rightChild(int index) {
          return 2 * index + 2;
      }
  
      // 返回[queryL, queryR]这个区间的值
      public E query(int queryL, int queryR) {
  
          if (queryL < 0 || queryL >= data.length || queryR < 0 || queryR >= data.length || queryL > queryR) {
              throw new IllegalArgumentException("Index is illegal.");
          }
  
          return query(0, 0, data.length - 1, queryL, queryR);
      }
  
      // 在以treeIndex为根的线段树的[l...r]范围里，寻找区间[queryL, queryR]的值
      private E query(int treeIndex, int l, int r, int queryL, int queryR) {
  
          if (l == queryL && r == queryR) {
              return tree[treeIndex];
          }
  
          int mid = l + (r - l) / 2;
          int leftTreeIndex = leftChild(treeIndex);
          int rightTreeIndex = rightChild(treeIndex);
  
          if (queryL >= mid + 1) {
              return query(rightTreeIndex, mid + 1, r, queryL, queryR);
          } else if (queryR <= mid) {
              return query(leftTreeIndex, l, mid, queryL, queryR);
          } else {
              E leftResult = query(leftTreeIndex, l, mid, queryL, mid);
              E rightResult = query(rightTreeIndex, mid + 1, r, mid + 1, queryR);
              return merger.merge(leftResult, rightResult);
          }
      }
  
      // 将index位置的值更新为e
      public void set(int index, E e) {
  
          if (index < 0 || index >= data.length) {
              throw new IllegalArgumentException("Index is illegal.");
          }
  
          data[index] = e;
          set(0, 0, data.length - 1, index, e);
  
      }
  
      // 在以treeIndex为根的线段树中更新index的值为e
      private void set(int treeIndex, int l, int r, int index, E e) {
  
          if (l == r) {
              tree[treeIndex] = e;
              return;
          }
  
          int mid = l + (r - l) / 2;
          int leftTreeIndex = leftChild(treeIndex);
          int rightTreeIndex = rightChild(treeIndex);
  
          if (index <= mid) {
              set(leftTreeIndex, l, mid, index, e);
          } else if (index >= mid + 1) {
              set(rightTreeIndex, mid + 1, r, index, e);
          }
  
          tree[treeIndex] = merger.merge(tree[leftTreeIndex], tree[rightTreeIndex]);
      }
  
      // 方便打印测试
      @Override
      public String toString() {
  
          StringBuilder res = new StringBuilder();
          res.append('[');
          for (int i = 0; i < tree.length; i++) {
              if (tree[i] != null) {
                  res.append(tree[i]);
              } else {
                  res.append("null");
              }
              if (i != tree.length - 1) {
                  res.append(", ");
              }
          }
          res.append(']');
          return res.toString();
      }
  }

• Merger接口的业务逻辑

• public interface Merger<E> {
  
      E merge(E a, E b);
  }

• 测试的业务逻辑

• public class Main {
  
      public static void main(String[] args) {
          Integer[] nums = {3, 6, -3, 2, -9};
          SegmentTree<Integer> segmentTree = new SegmentTree<>(nums, (a, b) -> a + b);
  
          System.out.println(segmentTree);
          System.out.println(segmentTree.getSize());
  
          // 测试查询
          System.out.println(segmentTree.query(0, 2));
          System.out.println(segmentTree.query(1, 4));
      }
  }

• 输出结果：

• [-1, 6, -7, 9, -3, 2, -9, 3, 6, null, null, null, null, null, null, null, null, null, null, null]
  5
  6
  -4