hackerrank Project Euler #210: Obtuse Angled Triangles

传送门

做出一个好几个星期屯下来的题目的感觉就是一个字：

爽！



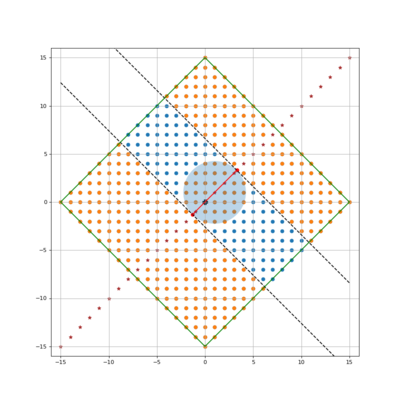
上图的黄点部分就是我们需要求的点

两边的部分很好算

求圆的地方有一个优化，由于圆心是整数点，我们可以把圆分为下面几个部分,阴影部分最难算，最后乘就好了

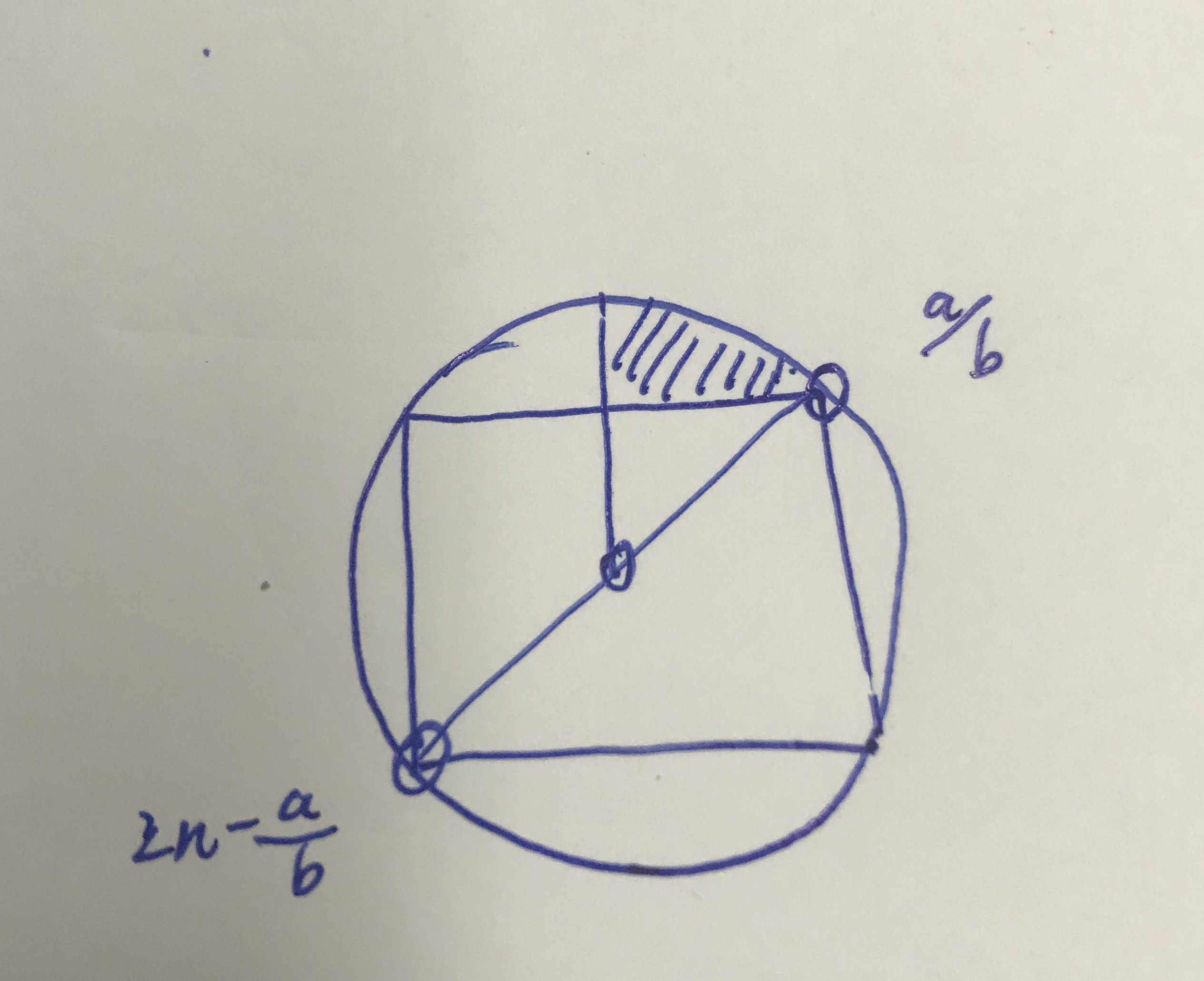
代码如下所示

#include <bits/stdc++.h>
using namespace std;
const int MAXN = 2005;
const int INF = 0x3f3f3f3f;
typedef long long ll;
typedef long double Double;
const Double tiny = 1e-20;

ll Ceil(Double x) {
    ll tt = ceil(x);
    if(abs(tt - x) < tiny) tt ++;
    return tt;
}

ll Floor(Double x) {
    ll tt = floor(x);
    if(abs(tt - x) < tiny) tt --;
    return tt;
}

int main() {
#ifdef LOCAL
    freopen("in.txt", "r", stdin);
#endif

    int r, a, b, n;
    while(~scanf("%d %d %d %d", &r, &a, &b, &n)) {
        Double leftEdge = Double(a*1.0)/b;
        Double rightEdge = 2*n - Double(a*1.0)/b;
        Double radiusTo2 = n - Double(a*1.0)/b;
        if(leftEdge > rightEdge) swap(leftEdge, rightEdge);
        ll sum = 0;

        Double leftDouble = r + 2*leftEdge;
        int leftInt = ceil(leftDouble);

        Double rightDouble = r - 2*rightEdge;
        int rightInt = ceil(rightDouble);

        sum += 1ll * (rightInt + leftInt) * r;
        if(rightInt % 2) sum += r & 1;
        if(leftInt % 2) sum += r & 1;
        // printf("%d %d %lld\n", leftInt, rightInt, sum);
        Double cirRadius = (rightEdge - leftEdge) / sqrt(2);
        // printf("%.3f\n", cirRadius);
        ll tmpSum = 0;
        for(int i = Floor(cirRadius), edge = ceil(radiusTo2); i >= edge; --i) {
            tmpSum += Floor(sqrt( (rightEdge - leftEdge)*(rightEdge - leftEdge) / 2 - 1ll*i*i));
            // tmpSum += Floor(sqrt( cirRadius * cirRadius - 1ll*i*i));
        }
        sum += tmpSum * 8;
        // printf("%lld\n", sum);
        sum += 1ll * Floor(cirRadius) * 4;
        // printf("%lld\n", sum);
        // printf("%.9f\n", (rightEdge - leftEdge)/2.0);
        sum += 1ll* Floor(radiusTo2) * Floor(radiusTo2) * 4;

        sum -= 1ll * Floor(n - leftEdge) * 2;

        printf("%lld\n", sum);
    }
    return 0;
}