题解 P3153 【[CQOI2009]跳舞】

P3153 [CQOI2009]跳舞

题目描述

一次舞会有n个男孩和n个女孩。每首曲子开始时，所有男孩和女孩恰好配成n对跳交谊舞。每个男孩都不会和同一个女孩跳两首（或更多）舞曲。有一些男孩女孩相互喜欢，而其他相互不喜欢（不会”单向喜欢“）。每个男孩最多只愿意和k个不喜欢的女孩跳舞，而每个女孩也最多只愿意和k个不喜欢的男孩跳舞。给出每对男孩女孩是否相互喜欢的信息，舞会最多能有几首舞曲？

输入输出格式

输入格式：

第一行包含两个整数n和k。以下n行每行包含n个字符，其中第i行第j个字符为'Y'当且仅当男孩i和女孩j相互喜欢。

输出格式：

仅一个数，即舞曲数目的最大值。

---

分析

首先看的出这道题是一个匹配问题，自然联想到网络流算法

既然是网络流，那么就一定有网络容量来达到限制的目的，最后对应题意的要求。而通过题意找限制条件，构建模型最后用最大流求解，是最大流类题目的核心解法

现在我们来看看这题有什么限制：

1.所有男孩/女孩都要跳舞，不能在旁边干看着

2.不会和同一人跳舞

3.只能和k个不喜欢的人跳舞

依据这些条件，我们怎么构建模型呢？

建模

我们一个一个分析：

1.都要跳舞

既然不能干看着，那么一首舞曲中，每个人都得跳，换言之，若是本题答案为ans，那么最终每人都能跳ans只舞，

所以我们二分答案，在某个模型下跑最大流，最后检查答案，若满足条件：（跳舞的总数就是ans * N（人数））我们就往上搜，否则就往下搜，不断缩小二分范围，找到答案 （其实貌似数据范围可以直接枚举）

2.不会和同一人跳舞

匹配的基本知识，男女连边容量为1即可，不再赘述

3.能和k个不喜欢的人跳舞

我们要求能跳舞的场数最多，自然就想k尽可能多一点，虽然k是不能改变的，但是依据贪心的思想，我们能不用k就尽量不用k，换言之，如果和舞伴互相喜欢，就不用消耗k的次数了。

为了达到喜欢的人互相跳舞不消耗k，我们需要分裂点：将每个男/女分裂为喜欢和不喜欢两个部分，然后连边如下图

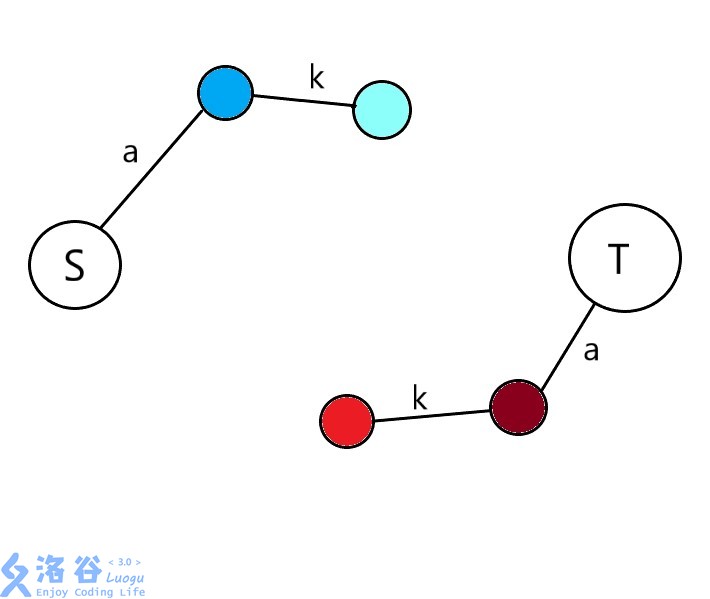
a为二分出来的答案

源点连男容量为a保证了一个人可以跳a场舞，来进行最大流以及答案验证

（深色为喜欢，浅一点为不喜欢）

若两人相互喜欢，则有：

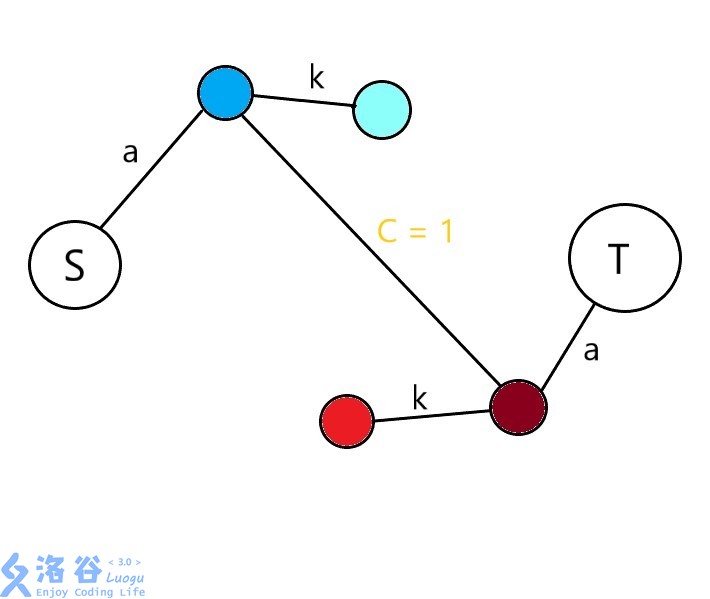
这样直接连喜欢，s到t的路上没有占用k，即k的次数无消耗；容量为1保证了只和同一人跳一次舞

---

若两人不互相喜欢，则有

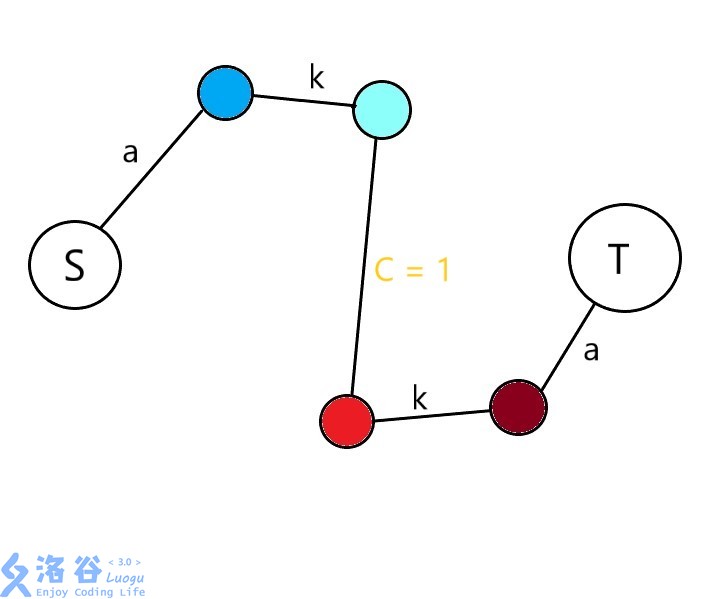
不喜欢的人跳舞不愿意，需要消耗k，路径被夹在k之间，最大流从之间通过消耗k，达到目的；容量为1同样保证了只和同一人跳一次舞

建模完毕

最后跑最大流，验证是否合法，继续二分即可得到最终答案

注：重复建图记得初始化

AC Code

#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
#include<algorithm>
#define ll long long
using namespace std;
int RD(){
    int out = 0,flag = 1;char c = getchar();
    while(c < '0' || c >'9'){if(c == '-')flag = -1;c = getchar();}
    while(c >= '0' && c <= '9'){out = out * 10 + c - '0';c = getchar();}
    return flag * out;
    }
const int maxn = 100019,INF = 1e9;
int num,k,nume = 1;
int dance[190][190];
int s,t,maxflow;
int head[maxn << 2];
struct Node{
    int v,dis,nxt;
    }E[maxn << 3];
void add(int u,int v,int dis){
    E[++nume].nxt = head[u];
    E[nume].v = v;
    E[nume].dis = dis;
    head[u] = nume;
    }
int d[maxn];
bool bfs(){
    queue<int>Q;
    memset(d,0,sizeof(d));
    d[s] = 1;
    Q.push(s);
    while(!Q.empty()){
        int u = Q.front();Q.pop();
        for(int i = head[u];i;i = E[i].nxt){
            int v = E[i].v;
            if(E[i].dis && !d[v]){
                d[v] = d[u] + 1;
                if(v == t)return 1;
                Q.push(v);
                }
            }
        }
    return 0;
    }
int Dinic(int u,int flow){
    if(u == t)return flow;
    int rest = flow,k;
    for(int i = head[u];i;i = E[i].nxt){
        int v = E[i].v;
        if(d[v] == d[u] + 1 && rest && E[i].dis){
            k = Dinic(v,min(rest,E[i].dis));
            if(!k)d[v] = 0;
            E[i].dis -= k;
            E[i ^ 1].dis += k;
            rest -= k;
            }
        }
    return flow - rest;
    }
void build(int a){
    memset(head,0,sizeof(head));
    nume = 1;//初始化
    for(int i = 1;i <= num;i++){
        add(s,i,a);
        add(i,s,0);//连汇点到男生喜欢
        add(i,i + num,k);
        add(i + num,i,0);//连男喜欢到不喜欢
        add(i + 2 * num,i + 3 * num,k);
        add(i + 3 * num,i + 2 * num,0);//连女不喜欢到喜欢
        add(i + 3 * num,t,a);
        add(t,i + 3 * num,0);//女喜欢到源点
        }
    for(int i = 1;i <= num;i++){
        for(int j = 1;j <= num;j++){
            if(dance[i][j]){
                add(i,j + 3 * num,1);
                add(j + 3 * num,i,0);
                }
            else{
                add(i + num,j + 2 * num,1);
                add(j + 2 * num,i + num,0);
                }
            }
        }
    }
bool check(int mid){
    build(mid);
    maxflow = 0;
    int flow = 0;
    while(bfs())while(flow = Dinic(s,INF))maxflow += flow;
    if(maxflow == mid * num)return 1;
    return 0;
    }
int search(int l,int r){
    int ans;
    while(l <= r){
        int mid = l + r >> 1;
        if(check(mid))l = mid + 1,ans = mid;
        else r = mid - 1;
        }
    return ans;
    }
int main(){
    num = RD();k = RD();
    char temp;
    for(int i = 1;i <= num;i++){
        for(int j = 1;j <= num;j++){
            cin>>temp;
            if(temp == 'Y')dance[i][j] = 1;
            }
        }
    s = num * 4 + 1;t = s + 1;
    printf("%d\n",search(0,num + k));
    return 0;
    }