线段树板子1（洛谷P3372）

传送

一道线段树板子（最简单的）

似乎之前在培训里写过线段树的样子？不记得了

何为线段树？

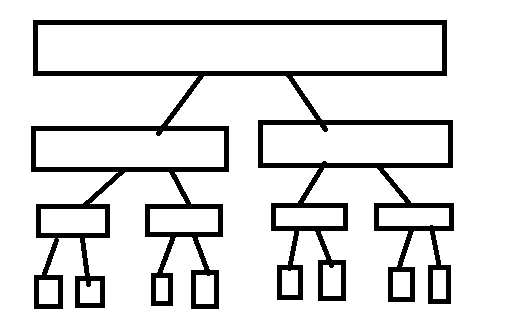
一般就是长成这样的树，树上的每个节点代表一个区间。线段树一般用于区间修改，区间查询的问题。

我们如何种写一棵线段树？

线段树包含：

1.建树

2.区间修改

3.区间查询与懒标记下传

---------------------------------------------------------------------

一些定义：

sum[k]:节点k所代表的区间的区间和（k是节点编号）

val[i]:在1到n的区间中，点i的权值

laz[k]:在k节点上打的懒标记

1.建树

从根节点开始，递归分别建左子树和右子树，当l=r时，sum[k]=val[l].我们注意到，对于每个不是叶子的节点来说，它的sum值为它的左二字+它的右儿子。同时线段树是一颗二叉树，所以节点k的左儿子的编号就是k*2,右儿子是k*2+1。所以，sum[k]=sum[k*2]+sum[k*2+1]。

2.区间修改

如果一个区间[l,r]要进行修改，那么与[l,r]有交集的节点都要修改。考虑到与[l,r]有交集的节点数为log(r-l+1)(如果出错欢迎指正)，如果直接修改每个点，则复杂度会很高，况且修改了以后还不一定会被查询到。为了降低复杂度，我们采用懒惰的思想。这时候，我们就有了懒标记。

在节点k上打上懒标记，代表k的子树中所有节点都加上laz[k],k节点的sum变为真实值。不过暂时先不真的在左右儿子节点加，如果查询到了，再加。这是待会要讲的标记下传。

所以，对于区间修改来说，我们唯一要做的就是找到被修改区间完全包含的区间，在这个节点上打个懒标记，然后维护一下打上标记的节点的sum(sum[k]+=laz[k]*(r-l+1))，就ok了。

如果当前区间并没有完全被包含，则继续递归寻找。判断它的左右儿子哪个与修改区间有交集，就修改哪个儿子，直到有完全被包含的区间出现。同时，对于当前的这个节点来说，还是要维护sum,sum[k]=sum[k*2]+sum[k*2+1](就是当前节点的sum=左儿子的sum+右儿子的sum)

3.区间查询与懒标记下传

当区间查询的时候，就不能再懒下去了（该干活了），这时候，我们就要把laz[k]扔给它的左儿子，右儿子，让他们变成真实值。

当然，如果没有懒标记（laz[k]=0）,那就直接结束了，就不管了。

如果当前区间并不完全被包含在查询区间里面，则递归查询。（要先懒标记下传）看它的哪个儿子与被查询区间有交集，就递归哪个儿子。

也正是因为上述原因，懒标记一次只下传一层（没有传到而要用到的节点会在递归查询中下传到）

在懒标记下传中，把懒标记传给它的左右儿子（不管是否与被查询区间有交集）。让它左右儿子的laz加上laz[k],然后维护他左右儿子的sum。(sum[2*k]+=laz[k]*(mid-l+1),sum[2*k+1]=laz[k]*(r-mid))

这样一棵线段树的基本操作就讲完辣。

代码：

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
using namespace std;
const long long N=;//小心毒瘤数据范围
long long n,m,val[N*],sum[N*],laz[N*];//注意数组大小
long long read()//读入long long(防毒瘤数据)
{
    char ch=getchar();
    int x=;bool f=;
    while(ch<''||ch>'')
    {
        if(ch=='-')f=;
        ch=getchar();
    }
    while(ch>=''&&ch<='')
    {
        x=(x<<)+(x<<)+(ch^);
        ch=getchar();
    }
    if(f)x=-x;
    return x;
}
int read2()//读入int(为了和函数的参数相匹配)
{
    char ch=getchar();
    int x=;bool f=;
    while(ch<''||ch>'')
    {
        if(ch=='-')f=;
        ch=getchar();
    }
    while(ch>=''&&ch<='')
    {
        x=(x<<)+(x<<)+(ch^);
        ch=getchar();
    }
    if(f)x=-x;
    return x;
}
void zj(int k,int l,int r,int v)//标记下传时候的增加（其实可以写进标记下传函数里面）
{
    laz[k]+=v;
    sum[k]+=v*(r-l+);
}
void pushdown(int k,int l,int r)//标记下传
{
    if(laz[k]==)return ;
    long long mid=(l+r)>>;
     zj(k<<,l,(int)mid,laz[k]);//位运算优化常数
     zj(k<<|,(int)mid+,r,laz[k]);
    laz[k]=;
}
void add(int k,int l,int r,int x,int y,int v)//将[x,y]这段区间加上v,l,r为当前递归到的节点代表的区间的左，右端点，k为当前节点编号
{

    if(l>=x&&r<=y)
    {
       laz[k]+=v;
       sum[k]+=v*(r-l+);
       return;
    }
    long long mid=(l+r)>>;
    pushdown(k,l,r);
    if(x<=mid)
      add(k<<,l,(int)mid,x,y,v);
    if(mid<y)
      add(k<<|,(int)mid+,r,x,y,v);
     sum[k]=sum[k<<]+sum[k<<|];// 维护和！！！
     return;
}
long long query(int k,int l,int r,int x,int y)//查询
{
    if(l>=x&&r<=y)//[l,r]被[x,y]完全覆盖
    {
        return sum[k];
    }
    long long mid=(l+r)>>,ans=;
    pushdown(k,l,r);
    if(x<=mid)//判断儿子是否有交集
      ans+=query(k<<,l,(int)mid,x,y);
    if(mid<y)
       ans+=query(k<<|,(int)(mid+),r,x,y);
    return ans;
}
void build(int k,int l,int r)//建树
{
    if(l==r)
    {
     sum[k]=val[l];
     return;
    }
    long long mid=(l+r)>>;
    build(k<<,l,(int)mid);
    build(k<<|,(int)(mid+),r);
    sum[k]=sum[k<<]+sum[k<<|];
    return;
}
int main()
{
    n=read();m=read();
    for(int i=;i<=n;i++)
      val[i]=read();
    build(,,n);
    for(int i=;i<=m;i++)
    {
        int cz,x,y;
        cz=read2();x=read2();y=read2();
        if(cz==)//修改
        {
            int k=read2();
            add(,,n,x,y,k);
        }
        else//查询
        {
             printf("%lld\n",query(,,n,x,y));
        }
    }
    return ;
}

线段树2（添加乘法操作，更带感）