POJ-1151-Atlantis(线段树+扫描线+离散化)[矩形面积并]

题意:求矩形面积并

分析:使用线段树+扫描线...因为坐标是浮点数的,因此还需要离散化!

把矩形分成两条边,上边和下边,对横轴建树,然后从下到上扫描上去,用col表示该区间有多少个下边,sum代表该区间内被覆盖的线段的长度总和

这里线段树的一个结点并非是线段的一个端点,而是该端点和下一个端点间的线段,所以题目中r+1,r-1的地方可以自己好好的琢磨一下

详细分析下扫描线

第一次完全看懂扫描线.

像这题的样例:

这么两个矩形,现在要求它的面积并.

假设我门将横边座位扫描线,即每个矩形有两条扫描线,下扫描线,下扫描线,

每条扫描线我们用结构体

const int MAXN=;
struct seg{
    double x1,x2,y;
    int flag;
    bool operator <(const seg& rsh)const{
        return y<rsh.y;
    }
}G[MAXN];

来保存,保存这条扫描线的两个横坐标和一个纵坐标,还用flag标记这条扫描线是上边还是下边,下边flag=1,上边flag=-1;

将扫描线都存好后,按照横坐标排序,使得每条边从下到上的顺序(a1,a2,a3,a4)

现在可以边看程序边看这..

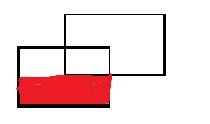
将a1插入线段树后计算a1覆盖的总长度sum[1]

则红色部分的面积就可以算出来了,sum[1]*(G[i+1].y-G[i].y)

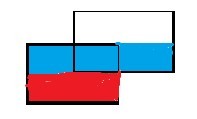
将a2插入线段树中,计算得到总长度为蓝色部分的底边,sum[1]

则蓝色部分的面积也就可以算出来了sum[1]*(G[i+1].y-G[i].y)

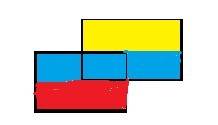
最后将a3插入树中,因为a3是上边,因此把红色的底边给消除了,这是线段树计算得的结果为黄色部分的底边sum[1]

则黄色部分的面积为sum[1]*(G[i+1].y-G[i].y)

如此,把三个部分的面积加起来就是矩形面积并了.这也就是扫描线计算计算面积并的基本过程了!

// File Name: 1151.cpp
// Author: Zlbing
// Created Time: 2013/7/20 14:36:01

#include<iostream>
#include<string>
#include<algorithm>
#include<cstdlib>
#include<cstdio>
#include<set>
#include<map>
#include<vector>
#include<cstring>
#include<stack>
#include<cmath>
#include<queue>
using namespace std;
#define CL(x,v); memset(x,v,sizeof(x));
#define INF 0x3f3f3f3f
#define LL long long
#define REP(i,r,n) for(int i=r;i<=n;i++)
#define RREP(i,n,r) for(int i=n;i>=r;i--)

#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1

const int MAXN=;
struct seg{
    double x1,x2,y;
    int flag;
    bool operator <(const seg& rsh)const{
        return y<rsh.y;
    }
}G[MAXN];
double hash[MAXN];

double sum[MAXN<<];
int col[MAXN<<];

void pushup(int rt,int l,int r)
{
    if(col[rt])
    {
        sum[rt]=hash[r+]-hash[l];
    }
    else if(l==r)sum[rt]=;
    else sum[rt]=sum[rt<<]+sum[rt<<|];
}

void update(int L,int R,int flag,int l,int r,int rt)
{
    if(L<=l&&R>=r)
    {
        col[rt]+=flag;
        pushup(rt,l,r);
        return;
    }
    int m=(l+r)>>;
    if(L<=m)update(L,R,flag,lson);
    if(R>m)update(L,R,flag,rson);
    pushup(rt,l,r);
}
int main()
{
    int cas=;
    int n;
    while(~scanf("%d",&n))
    {
        if(n==)break;
        int xlen=;
        double a,b,c,d;
        REP(i,,n)
        {
            scanf("%lf%lf%lf%lf",&a,&b,&c,&d);
            G[xlen].x1=a,G[xlen].x2=c,G[xlen].y=b,G[xlen].flag=;
            hash[xlen]=a;
            xlen++;
            hash[xlen]=c;
            G[xlen].x1=a,G[xlen].x2=c,G[xlen].y=d,G[xlen].flag=-;
            xlen++;
        }
        sort(G,G+xlen);
        sort(hash,hash+xlen);
        CL(col,);
        CL(sum,);
        double ans=;
        for(int i=;i<xlen-;i++)
        {
            int l=lower_bound(hash,hash+xlen,G[i].x1)-hash;
            int r=lower_bound(hash,hash+xlen,G[i].x2)-hash-;
            if(l<=r)update(l,r,G[i].flag,,xlen-,);
            ans+=sum[]*(G[i+].y-G[i].y);
        }
        printf("Test case #%d\n",cas++);
        printf("Total explored area: %.2lf\n\n",ans);
    }
    return ;
}