浅谈 Adaboost 算法

http://blog.csdn.net/haidao2009/article/details/7514787

菜鸟最近开始学习machine learning。发现adaboost 挺有趣，就把自己的一些思考写下来。

主要参考了http://stblog.baidu-tech.com/?p=19，其实说抄也不为过，但是我添加了一些我认为有意思的东西，所以我还是把它贴出来了，呵呵。

一 Boosting 算法的起源

boost 算法系列的起源来自于PAC Learnability(PAC 可学习性)。这套理论主要研究的是什么时候一个问题是可被学习的，当然也会探讨针对可学习的问题的具体的学习算法。这套理论是由Valiant提出来的，也因此（还有其他贡献哈）他获得了2010年的图灵奖。这里也贴出Valiant的头像，表示下俺等菜鸟的膜拜之情。哈哈哈

PAC 定义了学习算法的强弱

  弱学习算法---识别错误率小于1/2(即准确率仅比随机猜测略高的学习算法)

  强学习算法---识别准确率很高并能在多项式时间内完成的学习算法

同时 ,Valiant和 Kearns首次提出了 PAC学习模型中弱学习算法和强学习算法的等价性问题,即任意给定仅比随机猜测略好的弱学习算法 ,是否可以将其提升为强学习算法 ? 如果二者等价 ,那么只需找到一个比随机猜测略好的弱学习算法就可以将其提升为强学习算法 ,而不必寻找很难获得的强学习算法。 也就是这种猜测，让无数牛人去设计算法来验证PAC理论的正确性。

不过很长一段时间都没有一个切实可行的办法来实现这个理想。细节决定成败，再好的理论也需要有效的算法来执行。终于功夫不负有心人， Schapire在1996年提出一个有效的算法真正实现了这个夙愿，它的名字叫AdaBoost。AdaBoost把多个不同的决策树用一种非随机的方式组合起来，表现出惊人的性能！第一，把决策树的准确率大大提高，可以与SVM媲美。第二，速度快，且基本不用调参数。第三，几乎不Overfitting。我估计当时Breiman和Friedman肯定高兴坏了，因为眼看着他们提出的CART正在被SVM比下去的时候，AdaBoost让决策树起死回生！Breiman情不自禁地在他的论文里赞扬AdaBoost是最好的现货方法（off-the-shelf，即“拿下了就可以用”的意思）。(这段话摘自统计学习那些事)

了解了这段有意思的起源，下面来看adaboost算法应该会兴趣大增。

二 Boosting算法的发展历史（摘自http://stblog.baidu-tech.com/?p=19）

Boosting算法是一种把若干个分类器整合为一个分类器的方法，在boosting算法产生之前，还出现过两种比较重要的将多个分类器整合 为一个分类器的方法，即boostrapping方法和bagging方法。我们先简要介绍一下bootstrapping方法和bagging方法。

　　1）bootstrapping方法的主要过程

　　主要步骤：

　　i)重复地从一个样本集合D中采样n个样本

　　ii)针对每次采样的子样本集，进行统计学习，获得假设H_i

　　iii)将若干个假设进行组合，形成最终的假设H_final

　　iv)将最终的假设用于具体的分类任务

　　2）bagging方法的主要过程 -----bagging可以有多种抽取方法

　　主要思路：

　　i)训练分类器

　　从整体样本集合中，抽样n^* < N个样本 针对抽样的集合训练分类器C_i

　　ii)分类器进行投票，最终的结果是分类器投票的优胜结果

　　但是，上述这两种方法，都只是将分类器进行简单的组合，实际上，并没有发挥出分类器组合的威力来。直到1989年，Yoav Freund与 Robert Schapire提出了一种可行的将弱分类器组合为强分类器的方法。并由此而获得了2003年的哥德尔奖（Godel price）。

　　Schapire还提出了一种早期的boosting算法，其主要过程如下：

　　i)从样本整体集合D中，不放回的随机抽样n₁ < n个样本，得到集合 D₁

　　训练弱分类器C₁

　　ii)从样本整体集合D中，抽取 n₂ < n个样本，其中合并进一半被C₁ 分类错误的样本。得到样本集合D₂

　　训练弱分类器C₂

　　iii)抽取D样本集合中，C₁ 和 C₂ 分类不一致样本，组成D₃

　　训练弱分类器C₃

　　iv)用三个分类器做投票，得到最后分类结果

　　到了1995年，Freund and schapire提出了现在的adaboost算法，其主要框架可以描述为：

　　i)循环迭代多次

　　更新样本分布

　　寻找当前分布下的最优弱分类器

　　计算弱分类器误差率

　　ii)聚合多次训练的弱分类器

三 Adaboost 算法

AdaBoost 是一种迭代算法，其核心思想是针对同一个训练集训练不同的分类器，即弱分类器，然后把这些弱分类器集合起来，构造一个更强的最终分类器。(很多博客里说的三个臭皮匠赛过诸葛亮)

算法本身是改变数据分布实现的，它根据每次训练集之中的每个样本的分类是否正确，以及上次的总体分类的准确率，来确定每个样本的权值。将修改权值的新数据送给下层分类器进行训练，然后将每次训练得到的分类器融合起来，作为最后的决策分类器。

完整的adaboost算法如下

简单来说，Adaboost有很多优点:

　　1)adaboost是一种有很高精度的分类器

　　2)可以使用各种方法构建子分类器，adaboost算法提供的是框架

　　3)当使用简单分类器时，计算出的结果是可以理解的。而且弱分类器构造极其简单

　　4)简单，不用做特征筛选

　　5)不用担心overfitting！

四 Adaboost 举例

也许你看了上面的介绍或许还是对adaboost算法云里雾里的，没关系，百度大牛举了一个很简单的例子，你看了就会对这个算法整体上很清晰了。

　　下面我们举一个简单的例子来看看adaboost的实现过程：

　　图中，“+”和“-”分别表示两种类别，在这个过程中，我们使用水平或者垂直的直线作为分类器，来进行分类。

　　第一步：

　　根据分类的正确率，得到一个新的样本分布D_2­，一个子分类器h₁

　　其中划圈的样本表示被分错的。在右边的途中，比较大的“+”表示对该样本做了加权。

也许你对上面的ɛ1，ɑ1怎么算的也不是很理解。下面我们算一下，不要嫌我啰嗦，我最开始就是这样思考的，只有自己把算法演算一遍，你才会真正的懂这个算法的核心，后面我会再次提到这个。

算法最开始给了一个均匀分布 D 。所以h1 里的每个点的值是0.1。ok，当划分后，有三个点划分错了，根据算法误差表达式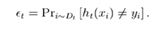得到 误差为分错了的三个点的值之和，所以ɛ1=(0.1+0.1+0.1)=0.3，而ɑ1 根据表达式 的可以算出来为0.42. 然后就根据算法 把分错的点权值变大。如此迭代，最终完成adaboost算法。

　　第二步：

　　根据分类的正确率，得到一个新的样本分布D₃，一个子分类器h₂

　　第三步：

　　得到一个子分类器h₃

　　整合所有子分类器：

　　因此可以得到整合的结果，从结果中看，及时简单的分类器，组合起来也能获得很好的分类效果，在例子中所有的。

五 Adaboost 疑惑和思考

到这里，也许你已经对adaboost算法有了大致的理解。但是也许你会有个问题，为什么每次迭代都要把分错的点的权值变大呢？这样有什么好处呢？不这样不行吗? 这就是我当时的想法，为什么呢？我看了好几篇介绍adaboost 的博客，都没有解答我的疑惑，也许大牛认为太简单了，不值一提，或者他们并没有意识到这个问题而一笔带过了。然后我仔细一想，也许提高错误点可以让后面的分类器权值更高。然后看了adaboost算法，和我最初的想法很接近，但不全是。 注意到算法最后的表到式为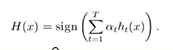，这里面的a 表示的权值，是由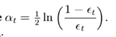得到的。而a是关于误差的表达式，到这里就可以得到比较清晰的答案了，所有的一切都指向了误差。提高错误点的权值，当下一次分类器再次分错了这些点之后，会提高整体的错误率，这样就导致 a 变的很小，最终导致这个分类器在整个混合分类器的权值变低。也就是说，这个算法让优秀的分类器占整体的权值更高，而挫的分类器权值更低。这个就很符合常理了。到此，我认为对adaboost已经有了一个透彻的理解了。

六 总结

　　最后，我们可以总结下adaboost算法的一些实际可以使用的场景：

　　1）用于二分类或多分类的应用场景

　　2）用于做分类任务的baseline

　　无脑化，简单，不会overfitting，不用调分类器

　　3）用于特征选择（feature selection)

　　4）Boosting框架用于对badcase的修正

　　只需要增加新的分类器，不需要变动原有分类器

　　由于adaboost算法是一种实现简单，应用也很简单的算法。Adaboost算法通过组合弱分类器而得到强分类器，同时具有分类错误率上界随着训练增加而稳定下降，不会过拟合等的性质，应该说是一种很适合于在各种分类场景下应用的算法。