深度学习面试题11:池化(same池化、valid池化、带深度的池化)
目录
Same最大值池化
多深度的same池化
Same平均值池化
Valid池化
参考资料
池化(Pooling)操作与卷积类似,取输入张量的每个位置的矩形领域内的最大值或平均值作为该位置的输出。
池化操作分为same池化和valid池化,同时还可以设置移动的步长
|
Same最大值池化 |
举例:4行4列的张量x和2行3列的掩码进行步长为1的same最大值池化,其过程如下

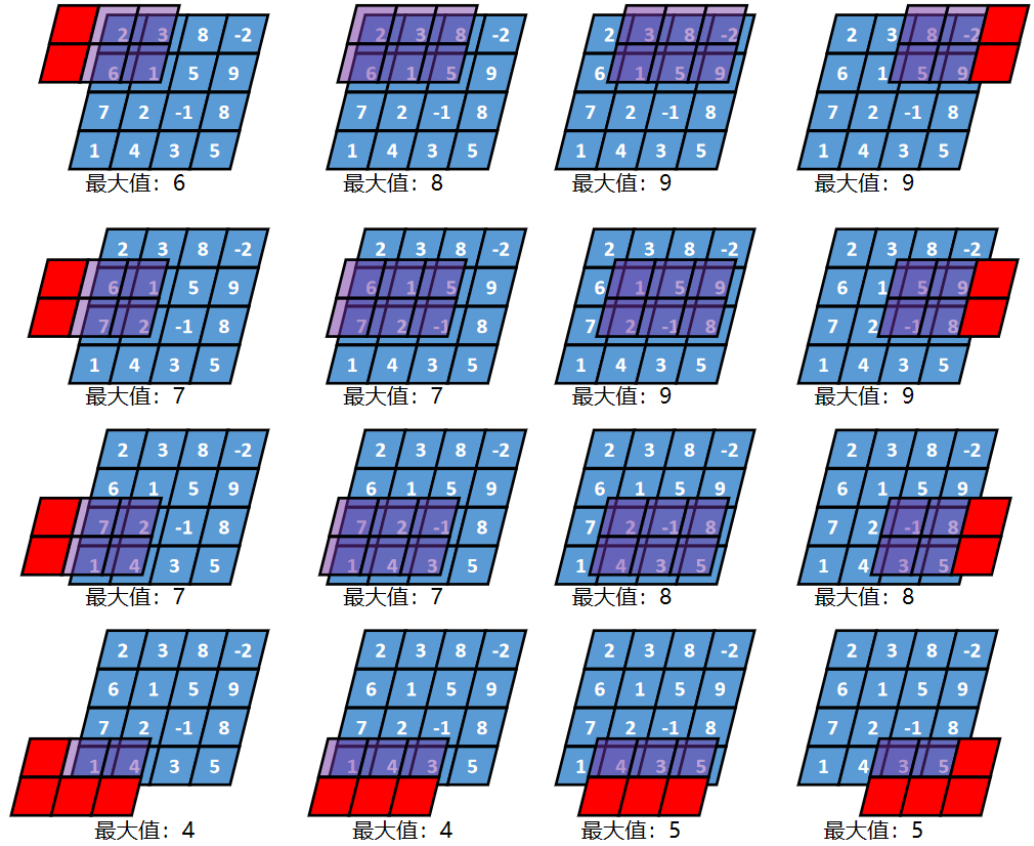
池化的结果是
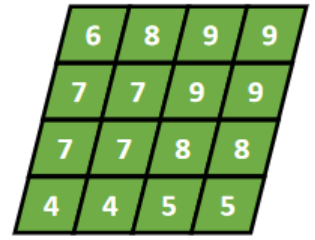
|
多深度的same池化 |
多深度的same池化是在每个深度上分别进行池化操作。
举例:3行3列2深度的张量和2行2列2深度的掩码进行步长为2的same最大值池化
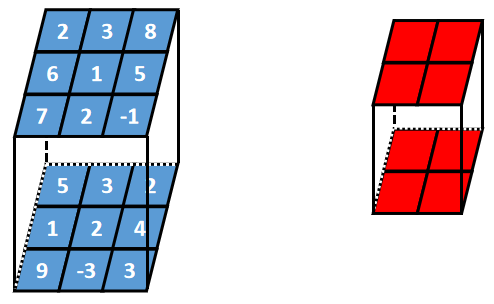

池化后不改变深度,结果为

|
Same平均值池化 |
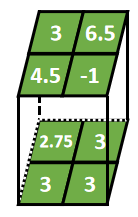
举例:3行3列2深度的张量和2行2列2深度的掩码进行步长为2的same平均值池化
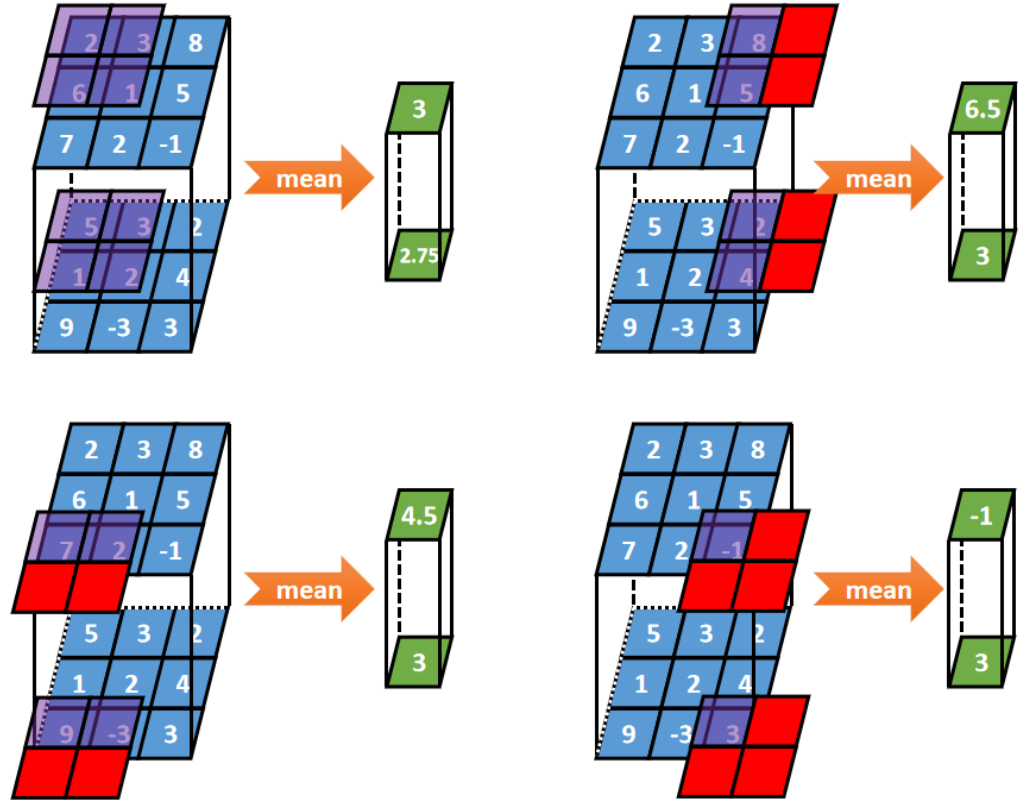
池化后不改变深度,结果为
|
Valid池化 |
Valid池化与same池化的不同之处在于掩码只在张量内移动,举例:4*4*1的张量x和2*2*1的掩码进行步长为1的valid最大值池化


结果为

|
参考资料 |
《图解深度学习与神经网络:从张量到TensorFlow实现》_张平
深度学习面试题11:池化(same池化、valid池化、带深度的池化)的更多相关文章
- 深度学习面试题13:AlexNet(1000类图像分类)
目录 网络结构 两大创新点 参考资料 第一个典型的CNN是LeNet5网络结构,但是第一个引起大家注意的网络却是AlexNet,Alex Krizhevsky其实是Hinton的学生,这个团队领导者是 ...
- 深度学习面试题29:GoogLeNet(Inception V3)
目录 使用非对称卷积分解大filters 重新设计pooling层 辅助构造器 使用标签平滑 参考资料 在<深度学习面试题20:GoogLeNet(Inception V1)>和<深 ...
- 深度学习与计算机视觉(11)_基于deep learning的快速图像检索系统
深度学习与计算机视觉(11)_基于deep learning的快速图像检索系统 作者:寒小阳 时间:2016年3月. 出处:http://blog.csdn.net/han_xiaoyang/arti ...
- 深度学习面试题27:非对称卷积(Asymmetric Convolutions)
目录 产生背景 举例 参考资料 产生背景 之前在深度学习面试题16:小卷积核级联卷积VS大卷积核卷积中介绍过小卷积核的三个优势: ①整合了三个非线性激活层,代替单一非线性激活层,增加了判别能力. ②减 ...
- 深度学习面试题17:VGGNet(1000类图像分类)
目录 VGGNet网络结构 论文中还讨论了其他结构 参考资料 2014年,牛津大学计算机视觉组(Visual Geometry Group)和Google DeepMind公司的研究员一起研发出了新的 ...
- 深度学习面试题12:LeNet(手写数字识别)
目录 神经网络的卷积.池化.拉伸 LeNet网络结构 LeNet在MNIST数据集上应用 参考资料 LeNet是卷积神经网络的祖师爷LeCun在1998年提出,用于解决手写数字识别的视觉任务.自那时起 ...
- 深度学习面试题26:GoogLeNet(Inception V2)
目录 第一层卷积换为分离卷积 一些层的卷积核的个数发生了变化 多个小卷积核代替大卷积核 一些最大值池化换为了平均值池化 完整代码 参考资料 第一层卷积换为分离卷积 net = slim.separab ...
- 深度学习面试题20:GoogLeNet(Inception V1)
目录 简介 网络结构 对应代码 网络说明 参考资料 简介 2014年,GoogLeNet和VGG是当年ImageNet挑战赛(ILSVRC14)的双雄,GoogLeNet获得了第一名.VGG获得了第二 ...
- 深度学习面试题18:网中网结构(Network in Network)
目录 举例 参考资料 网中网结构通过多个分支的运算(卷积或池化),将分支上的运算结果在深度上连接 举例 一个3*3*2的张量, 与3个1*1*2的卷积核分别same卷积,步长=1, 与2个2*2*2的 ...
随机推荐
- python 标准库subprocess
作者:Vamei 出处:http://www.cnblogs.com/vamei subprocess包主要功能是执行外部的命令和程序.subprocess的功能与shell类似.subprocess ...
- Vue检测当前是否处于mock模式
Vue检测当前是否处于mock模式 1.在main.js中声明全局变量: import Vue from 'vue' /* 全局变量 */ var GLOBAL_VARIABLE = { isMock ...
- 初识面向对象(钻石继承,super,多态,封装,method,property,classmethod,staticmethod)
组合 什么有什么的关系 一个类的对象作为另一个类的对象继承 子类可以使用父类中的名字(静态属性 方法)抽象类和接口类 只能不继承,不能被实例化 子类必须实现父类中的同名方法———规范代码 metacl ...
- 【HICP Gauss】数据库 环境的搭建 -1
1.安装规则 1.主机名必须网络唯一 2.主机名必须两位数以上 可以中划线 不能下划线 3.固定IP地址 4.端口号 1888 新增账户 omm 用户组 dbgrp ,家目录 /home/ ...
- Android AIDL使用详解_Android IPC 机制详解
一.概述 AIDL 意思即 Android Interface Definition Language,翻译过来就是Android接口定义语言,是用于定义服务器和客户端通信接口的一种描述语言,可以拿来 ...
- c++第四次作业
继承与派生--访问控制 一.知识要点 (一)知识回顾: 基类的成员可以有public.protected.private三种访问属性.基类的自身成员可以对基类中任何一个其他成员进行访问,但是通过基类的 ...
- mingw控制台中文乱码
乱码原因 直接先用一段话讲乱码原因,看不懂老老实实就往下看吧 其实我用Sublime或者VSCode等编辑器写代码出现的控制台中文乱码问题是编译器mingw输出的数据使用的是UTF-8编码,而控制台用 ...
- [转]Linux网络 - 数据包的发送过程
转, 原文:https://segmentfault.com/a/1190000008926093 -------------------------------------------------- ...
- “只有DBA才能导入由其他DBA导出的文件”各种解决办法
“只有DBA才能导入由其他DBA导出的文件”各种解决办法 当oracle导入的时候出现“只有 DBA 才能导入由其他 DBA 导出的文件”的时候通常有以下几种解决办法! 1:常见的是直接grant ...
- 接口-httpClient
最近在工作的过程中有遇到httpClient接口,今天特意些一个小示例对这个知识点进行温习. 下面是代码小片段: package com.sinosoft.lis.mgubq.zhaoyongqian ...
