UVA 221 Urban Elevations

思路：

　　一些解释：

　　①：建筑的排序：

　　下面是以输入顺序为标号，在数组bd中的顺序：

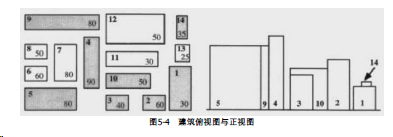
　　排序后在数组bd中的顺序：

　　

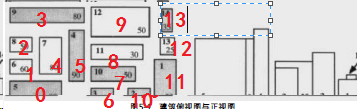
　　以后我们比较就按这个顺序

　　②：x坐标的排序

　　x的内容是每一个建筑的左边界和右边界，我们把他去重排序后，就是一个一个的坐标，相邻的x形成一个区间，

　　取它的中点来判断，比如，样例输入的bd[1]就是遍历所有的区间来判断是否可见。下面附上调试截图。

　　x:

　　

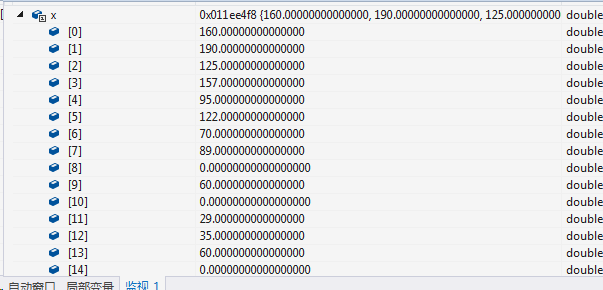
　　sort后的x:

　　

　　unique后的x:

　　

　　

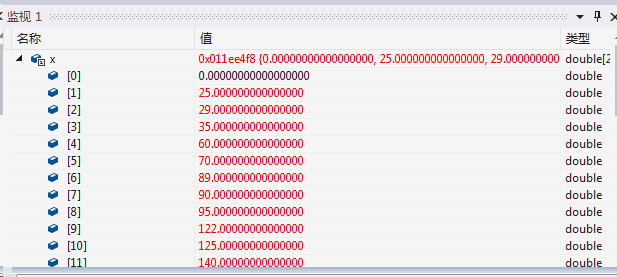
 #include<cstdio>
 #include<algorithm>
 using namespace std;
 struct building {
     int NO;
     double x, y, width, depth, height;
     double xr;//右边界
 }bd[];
 double x[ * ];
 int n;
 bool cmp(building & b1, building & b2)
 {
     if (b1.x < b2.x)
         return true;
     if (b1.x == b2.x&&b1.y < b2.y)
         return true;
     return false;
 }
 bool cover(int i, double mx)//看mx在不在第i个建筑范围内
 {
     return  ((bd[i].x <= mx) && (bd[i].xr >= mx));
 }
 bool visible(int i, double mx)//第i个建筑物在x=mx是否可见
 {
     if (!cover(i, mx))
         return false;
     for (int j = ; j < n; j++)//遍历所有建筑,寻找第i个建筑[南方]的建筑看会不会被挡住
     {
         if (bd[j].y < bd[i].y&&bd[j].height >= bd[i].height&&cover(j,mx))
             return false;
         /*bd[j].y < bd[i].y在此建筑的南方
         bd[j].height >= bd[i].height，南方建筑更高
         cover(j,mx) mx也在南方建筑范围内
         */
     }
     return true;
 }
 int main()
 {
     int kase = ;
     while (scanf("%d", &n) && n != )
     {
         for (int i = ; i < n; i++)
         {
             scanf("%lf%lf%lf", &bd[i].x, &bd[i].y, &bd[i].width);
             scanf("%lf%lf", &bd[i].depth, &bd[i].height);
             bd[i].NO = i+;
             bd[i].xr = bd[i].x + bd[i].width;
             x[i * ] = bd[i].x;//记录左边界
             x[i *  + ] = bd[i].xr;//右边界
         }

         sort(bd, bd + n, cmp);
         sort(x, x +  * n);
         int m = unique(x, x + n * ) - x;//不重复元素的个数
         if (kase++)
             printf("\n");
         printf("For map #%d, the visible buildings are numbered as follows:\n%d", kase,bd[].NO);
         //因为第一个输出没有空格，而第一个bd肯定不会被挡住，
         //所有先把第一个输出来.下面从1开始
         for (int i = ; i < n; i++)
         {
             bool vis = false;
             for (int j = ; j < m-; j++)
             {
                 if (visible(i, (x[j] + x[j+]) / ))
                 {
                     vis = true;
                     break;
                 }
             }
             if (vis)
                 printf(" %d", bd[i].NO);
         }
         printf("\n");
     }
     return ;
 }