HDU 4780 Candy Factory(拆点费用流)

Problem Description

  A new candy factory opens in pku-town. The factory import M machines to produce high quality candies. These machines are numbered from 1 to M.
  There are N candies need to be produced. These candies are also numbered from 1 to N. For each candy i , it can be produced in any machine j. It also has a producing time(s_i,t_i) , meaning that candy i must start producing at time s_i and will finish at t_i. Otherwise if the start time is p_i(s_i < p_i < t_i) then candy will still finish at t_i but need additional K*(p_i - s_i) cost. The candy can’t be produced if p_i is greater than or equal to t_i. Of course one machine can only produce at most one candy at a time and can’t stop once start producing.
  On the other hand, at time 0 all the machines are in their initial state and need to be “set up” or changed before starting producing. To set up Machine j from its initial state to the state which is suitable for producing candiy i, the time required is C_ij and cost is D_ij. To change a machine from the state suitable for candy i₁ into the state suitable for candy i₂, time required is E_i1i2 and cost is F_i1i2.
  As the manager of the factory you have to make a plan to produce all the N candies. While the sum of producing cost should be minimized.

 

Input

　　There are multiple test cases.
　　For each case, the first line contains three integers N(1<=N<=100), M(1<=M<=100), K(1<=K<=100) . The meaning is described above.
　　Then N lines follow, each line contains 2 integers s_i and t_i(0 <= s_i < t_i <100000).
　　Then N lines follow, each line contains M integers, the j-th integer of the i-th line indicating C_ij(1<=C_ij<=100000) .
　　Then N lines follow, each line contains M integers, the j-th integer of the i-th line indicating D_ij(1<=D_ij<=100000) .
　　Then N lines follow, each line contains N integers, the i₂-th integer of the i₁-th line indicating E_i1i2(1<=E_i1j2<=100000) . 
　　Then N lines follow, each line contains N integers, the i₂-th integer of the i₁-th line indicating F_i1i2(1 <= F_i1j2<=100000) . 
　　Since the same candy will only be produced once, E_ii and F_ii are meaningless and will always be -1.
　　The input ends by N=0 M=0 K=0. Cases are separated with a blank line.

 

Output

For each test case, if all of M candies can be produced, output the sum of minimum producing cost in a single line. Otherwise output -1.

 

Sample Input

3 2 1
4 7
2 4
8 9
4 4
3 3
3 3
2 8
12 3
14 6
-1 1 1
1 -1 1
1 1 -1
-1 5 5
5 -1 5
5 5 -1

1 1 2
1 5
5
5
-1
-1

0 0 0

 

Sample Output

11
-1

Hint

For the first example, the answer can be achieved in the following way: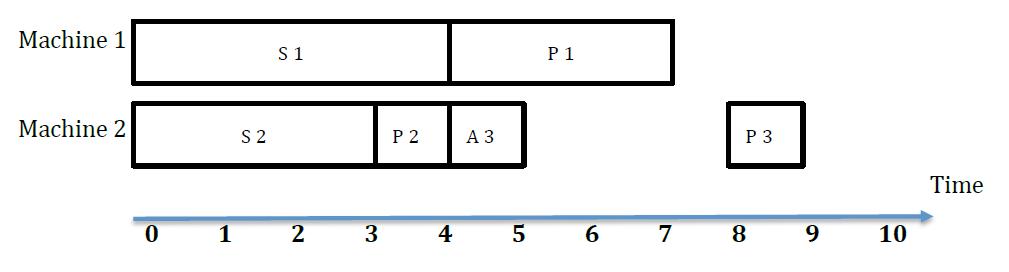
In the picture, S i represents setting up time for candy i, A i represents changing time for candy i and P i represents producing time for candy i .
So the total cost includes: 

setting up machine 1 for candy 1, costs 2

setting up machine 2 for candy 2, costs 3

changing state from candy 2 to candy 3, costs 5

late start of candy 2, costs 1

题意

有N个糖果需要被生产，有M个机器，K代表额外花费系数

N行代表第i个糖果只能在[s[i],t[i]]的时间内被生产

接下来N*M代表生产第i个糖果的机器j在C[i][j]时间被开启

接下来N*M代表生产糖果i机器j的基础花费D[i][j]，如果在第s[i]<p<t[i]的时间开始生产，也可以在t[i]生产出糖果，但需要额外花费(p-s[i])*K的花费

接下来N*N代表把机器J正在生产i糖果改成生产j糖果，所需的额外时间为E[i][j]

接下来N*N代表把机器J正在生产i糖果改成生产j糖果，所需的基础花费F[i][j]，如果在第s[j]<p<t[j]的时间开始生产，也可以在t[j]生产出糖果，但需要额外花费(p-s[j])*K的花费

题解

一道比较复杂的费用流题，题意读了很久

为了保证糖果从源点S流出一次从汇点T流入一次，可以把N个糖果拆成左右糖，然后(S,左糖,1,0)，然后(右糖,T,1,0)

然后考虑一个机器生产完i再去生产j的情况，如果时间允许，就连(左糖i，右糖j，1，基础花费F+额外花费)

然后新建一个点u，(S,u,m,0)，(u,每个机器,1,0)，如果机器i生产糖果j的时间C[j][i]<t[j]就连线(机器,右糖,1,基础花费D+额外花费)

代码

 #include<bits/stdc++.h>
 using namespace std;

 const int N=1e5+;
 const int M=2e5+;
 const int INF=0x3f3f3f3f;

 int FIR[N],FROM[M],TO[M],CAP[M],FLOW[M],COST[M],NEXT[M],tote;
 int pre[N],dist[N],q[];
 bool vis[N];
 int n,m,S,T;
 void init()
 {
     tote=;
     memset(FIR,-,sizeof(FIR));
 }
 void addEdge(int u,int v,int cap,int cost)
 {
     FROM[tote]=u;
     TO[tote]=v;
     CAP[tote]=cap;
     FLOW[tote]=;
     COST[tote]=cost;
     NEXT[tote]=FIR[u];
     FIR[u]=tote++;

     FROM[tote]=v;
     TO[tote]=u;
     CAP[tote]=;
     FLOW[tote]=;
     COST[tote]=-cost;
     NEXT[tote]=FIR[v];
     FIR[v]=tote++;
 }
 bool SPFA(int s, int t)
 {
     memset(dist,INF,sizeof(dist));
     memset(vis,false,sizeof(vis));
     memset(pre,-,sizeof(pre));
     dist[s] = ;vis[s]=true;q[]=s;
     int head=,tail=;
     while(head!=tail)
     {
         int u=q[++head];vis[u]=false;
         for(int v=FIR[u];v!=-;v=NEXT[v])
         {
             if(dist[TO[v]]>dist[u]+COST[v]&&CAP[v]>FLOW[v])
             {
                 dist[TO[v]]=dist[u]+COST[v];
                 pre[TO[v]]=v;
                 if(!vis[TO[v]])
                 {
                     vis[TO[v]] = true;
                     q[++tail]=TO[v];
                 }
             }
         }
     }
     return pre[t]!=-;
 }
 void MCMF(int s, int t, int &cost, int &flow)
 {
     flow=;
     cost=;
     while(SPFA(s,t))
     {
         int Min=INF;
         for(int v=pre[t];v!=-;v=pre[TO[v^]])
             Min=min(Min,CAP[v]-FLOW[v]);
         for(int v=pre[t];v!=-;v=pre[TO[v^]])
         {
             FLOW[v]+=Min;
             FLOW[v^]-=Min;
             cost+=COST[v]*Min;
         }
         flow+=Min;
     }
 }
 int main()
 {
     int N,M,K,u,ss[],tt[],C[][],D[][],E[][],F[][];
     while(scanf("%d%d%d",&N,&M,&K)!=EOF,N||M||K)
     {
         init();
         for(int i=;i<=N;i++)
             scanf("%d%d",&ss[i],&tt[i]);
         for(int i=;i<=N;i++)for(int j=;j<=M;j++)
             scanf("%d",&C[i][j]);
         for(int i=;i<=N;i++)for(int j=;j<=M;j++)
             scanf("%d",&D[i][j]);
         for(int i=;i<=N;i++)for(int j=;j<=N;j++)
             scanf("%d",&E[i][j]);
         for(int i=;i<=N;i++)for(int j=;j<=N;j++)
             scanf("%d",&F[i][j]);

         S=,u=N+N+M+,T=N+N++M+,n=T;
         for(int i=;i<=N;i++)
         {
             addEdge(S,i,,);
             addEdge(N+i,T,,);
             for(int j=;j<=N;j++)
             {
                 if(i!=j&&tt[i]+E[i][j]<tt[j])
                 {
                     int c=(max(tt[i]+E[i][j],ss[j])-ss[j])*K;
                     addEdge(i,N+j,,c+F[i][j]);
                 }
             }
         }
         addEdge(S,u,M,);
         for(int i=;i<=M;i++)
         {
             addEdge(u,N+N+i,,);
             for(int j=;j<=N;j++)
             {
                 if(C[j][i]<tt[j])
                 {
                     int c=(max(C[j][i],ss[j])-ss[j])*K;
                     addEdge(N+N+i,N+j,,c+D[j][i]);
                 }
             }
         }
         int flow,cost;
         MCMF(S,T,cost,flow);
         if(flow!=N)printf("-1\n");
         else printf("%d\n",cost);
     }
     return ;
 }