Cocos Creator 中 _worldMatrix 到底是什么(上)

1. (矩阵)Matrix是什么，有什么用

(矩阵)Matrix一个神奇的存在？在开发过程中对里边各项值的含义是不是抓耳挠腮，百思不得其解？今天我们就来庖丁解牛，拨开它的神秘面纱。由于内容较多，关于Cocos Creator 中的_worldMatrix会分为三篇文章完成。最终形成一个完整的demo

首先我们先看看在Cocos Creator编辑器中，对应图形的变化都有那些属性，如下图

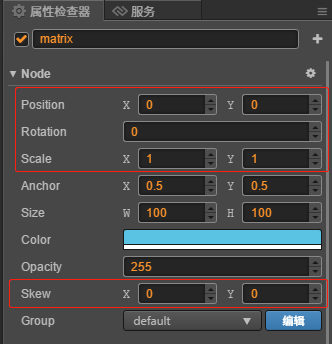
红框的地方分别是位移、旋转、缩放、倾斜它们都一一对应一个变换矩阵。

Cocos Creator 中的（矩阵）Matrix 是一个长度16的一维数组，按照先列后行的顺序存储一个 4 x 4 的放方阵。数组索引 0 1 2 3 分别表示矩阵第一列第1 2 3 4 行的数据。在2d的游戏坐标系中，一个三维矩阵就可以满足基本的变换，但cocos creator 采用了四维矩阵，应该是为了和3d保持一致。矩阵表示如下(左边体现Mat4对应属性排列位置。右边表示代码中经常用到的变量a b c d tx ty与矩阵对应的位置信息)

$$
\left[
\begin{matrix}
m00&m04&m08&m12\
m01&m05&m09&m13\
m02&m06&m10&m14\
m03&m07&m11&m15\
\end{matrix}
\right]
=>
\left[
\begin{matrix}
a&c&0&0\
b&d&0&0\
0&0&1&0\
tx&ty&tz&1
\end{matrix}
\right]
$$

这样的信息有什么用呢？用来存储节点 旋转 缩放 倾斜 平移的图形变换信息。要想知道其中缘由，复习一下线性代数及高数是很有必要的

矩阵乘法，以及相关性质
单位矩阵、逆矩阵、矩阵转置
向量
齐次坐标
三角函数

有了以上知识，我们就可以简单的推导下2d情况下，图形变换对应的4中情况

2. 旋转矩阵推导

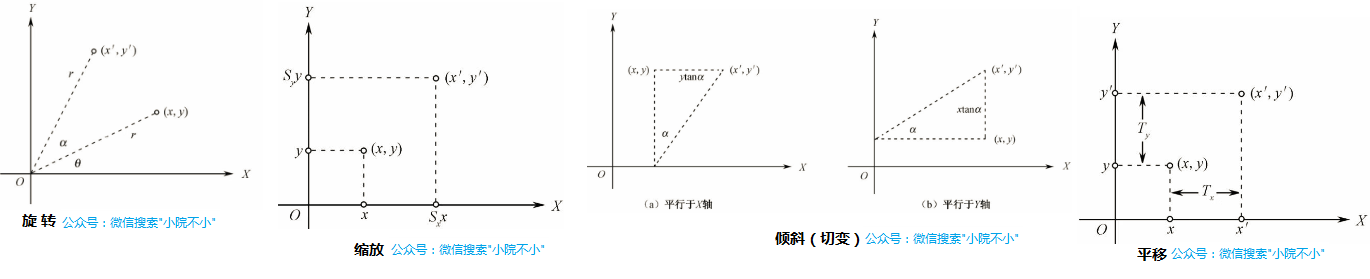
在2d坐标系中，假设存在点（x,y）,我们将该点同原点（0，0）相连形成一个线段。此时线段与坐标系中x轴的弧度为a 。我们将在以原点为圆心,线段的长度半径r。逆时针旋转弧度 b，该条线段另外一端坐标变为（x1,y1)，如下图(左1)

三个函数相关知识

正弦函数和余弦函数
sin(a)=y/r => y = rsin(a)
cos(a)=x/r => x = rcos(a)
和角公式
cos(a+b) = cos(a)cos(b) - sin(a)sin(b)
sin(a+b) = sin(a)cos(b) + cos(a)sin(b)

由三角函数可以推导出
x1 = rcos(a+b) = rcos(a)cos(b) - rsin(a)sin(b) = xcos(b) - ysin(b)
y1 = rsin(a+b) =rsin(a)cos(b) + rcos(a)sin(b) = ycos(b) + xsin(b) = xsin(b)+ysin(b)
转换矩阵形式 B=AX

$$
\left[
\begin{matrix}
x1\y1\1
\end{matrix}
\right]
=
\left[
\begin{matrix}
cos(b)&-sin(b)&0\
sin(b)&cos(b)&0\
0&0&1
\end{matrix}
\right]
\times
\left[
\begin{matrix}
x\y\1
\end{matrix}
\right]
$$

在cocos creator中，采用行矩阵的写法。以上在cocos creator实际运行形式如下,转换公式如下 $B^T=X^T*A^T$。cocos creator 中剩下的缩放，倾斜，平移，请按照转置矩阵，自行推导。

$$
\left[
\begin{matrix}
x1&y1&1
\end{matrix}
\right]
=
\left[
\begin{matrix}
x&y&1
\end{matrix}
\right]
\times
\left[
\begin{matrix}
cos(b)&sin(b)&1\
-sin(b)&cos(b)&1\
0&0&1
\end{matrix}
\right]
$$

3. 缩放矩阵推导

在2d坐标系中，假设存在点（x,y）缩放就是将坐标的x或y分别乘以一个缩放因子sx或sy。得到一个新的坐标（x1,y1），如下图左2。

由此可得到缩放公式
x1=xsx = xsx + y0
y1=xsy = x0 + ysy
转换矩阵形式 B=AX

$$
\left[
\begin{matrix}
x1\y1\1
\end{matrix}
\right]
=
\left[
\begin{matrix}
sx&0&0\
0&sy&0\
0&0&1
\end{matrix}
\right]
\times
\left[
\begin{matrix}
x\y\1
\end{matrix}
\right]
$$

4. 倾斜矩阵推导

在2d坐标系中，假设存在点（x,y）倾斜分为x轴倾斜以及y轴倾斜。沿x轴倾斜，就是将该点与点（x,0）连接而成的线段，以（x,0）为圆心，旋转弧度a。如下图（左3，左4）得到一个新的坐标（x1,y1）。

由此可得到倾斜公式

沿x轴倾斜弧度a （图左3）
x1=x+ytan(a)
y1=y
转换矩阵形式 B=AX

$$
\left[
\begin{matrix}
x1\y1\1
\end{matrix}
\right]
=
\left[
\begin{matrix}
1&tan(a)&0\
0&1&0\
0&0&1
\end{matrix}
\right]
\times
\left[
\begin{matrix}
x\y\1
\end{matrix}
\right]
$$

沿y轴倾斜弧度a （图左4）
x1=x
y1=y+xtan(a)=xtan(a)+y
转换矩阵形式 B=AX

$$
\left[
\begin{matrix}
x1\y1\1
\end{matrix}
\right]
=
\left[
\begin{matrix}
1&0&0\
tan(a)&1&0\
0&0&1
\end{matrix}
\right]
\times
\left[
\begin{matrix}
x\y\1
\end{matrix}
\right]
$$

5. 平移矩阵推导

在2d坐标中，假设存在点（x,y）平移分别是将 x 或 y 加上 x方向位移 tx 或 y方向位移 ty。从而得到新的点坐标（x1,y1）(图左5)

此可得到公式

x1=x+tx
y1=y+ty

转换矩阵形式 B=AX

$$
\left[
\begin{matrix}
x1\y1\1
\end{matrix}
\right]
=
\left[
\begin{matrix}
1&0&tx\
0&1&ty\
0&0&1
\end{matrix}
\right]
\times
\left[
\begin{matrix}
x\y\1
\end{matrix}
\right]
$$

6. 复合变换

将变换矩阵，依次相乘得到一个新的矩阵记为$T_c$，使得$B=X*T_c$。所以**Cocos Creator中的，_worldMatrix，就是当前节点在世界坐标系中对应的复合变换矩阵**$T_c$。矩阵的乘法不满足交换律。所以不同的顺序，变换的效果会不相同。

7.小结

未完待续，中篇，我将分析CCNode.js 中 _updateLocalMatrix 方法为切入点，来加强对Cocos Creator 中 _worldMatrix理解。下篇，利用理解的知识完成图形变换demo。再次加强对_worldMatrix认知。

欢迎感兴趣的朋友关注我的微信订阅号"小院不小"，或者点击下方的二维码关注。我将多年开发中遇到的难点，以及一些有意思的功能，体会都会一一发布到我的订阅号中。需要本文demo可以在公众号中回复matrix

维护了一个Coscos Creator 的游戏开发群，欢迎喜欢聊技术的朋友加入

闲来无事，采用cocos creator开发了一个小游戏【坦克侠】，感兴趣的朋友一个可以来玩玩